Návod: Násobení matic
Tento podrobný návod ukazuje, jak pomocí C++ AMP zrychlit provádění násobení matice. Jsou prezentovány dva algoritmy, jeden bez provazování a jeden s provazování.
Požadavky
Než začnete, potřebujete:
- Přečtěte si přehled C++ AMP.
- Čtení pomocí dlaždic
- Ujistěte se, že používáte alespoň Windows 7 nebo Windows Server 2008 R2.
Poznámka:
Hlavičky C++ AMP jsou zastaralé od sady Visual Studio 2022 verze 17.0.
Zahrnutím všech hlaviček AMP se vygenerují chyby sestavení. Před zahrnutím záhlaví AMP definujte _SILENCE_AMP_DEPRECATION_WARNINGS upozornění.
Vytvoření projektu
Pokyny k vytvoření nového projektu se liší podle toho, jakou verzi sady Visual Studio máte nainstalovanou. Pokud chcete zobrazit dokumentaci pro upřednostňovanou verzi sady Visual Studio, použijte ovládací prvek selektoru verzí . Nachází se v horní části obsahu na této stránce.
Vytvoření projektu v sadě Visual Studio
Na řádku nabídek zvolte Soubor>nový>projekt a otevřete dialogové okno Vytvořit nový projekt.
V horní části dialogového okna nastavte jazyk na C++, nastavte platformu pro Windows a nastavte typ projektu na konzolu.
V filtrovaném seznamu typů projektů zvolte Prázdný projekt a pak zvolte Další. Na další stránce zadejte do pole Název matrixMultiply název projektu a v případě potřeby zadejte umístění projektu.
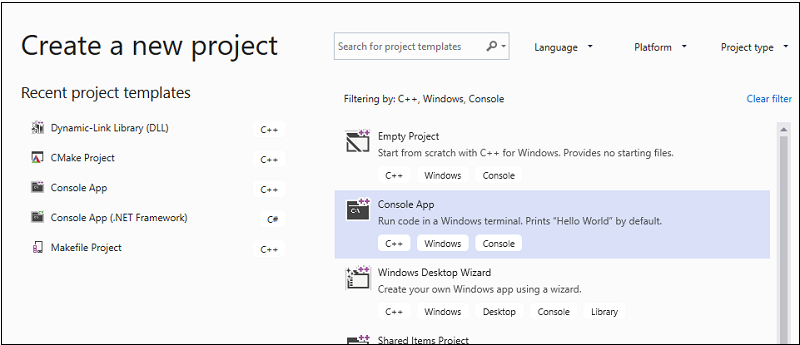
Zvolte tlačítko Vytvořit a vytvořte projekt klienta.
V Průzkumník řešení otevřete místní nabídku pro zdrojové soubory a pak zvolte Přidat>novou položku.
V dialogovém okně Přidat novou položku vyberte soubor C++ (.cpp), do pole Název zadejte MatrixMultiply.cpp a pak zvolte tlačítko Přidat.
Vytvoření projektu v sadě Visual Studio 2017 nebo 2015
Na řádku nabídek v sadě Visual Studio zvolte Soubor>nový>projekt.
V části Nainstalováno v podokně šablon vyberte Visual C++.
Vyberte Prázdný projekt, do pole Název zadejte MatrixMultiply a pak zvolte tlačítko OK.
Zvolte tlačítko Další.
V Průzkumník řešení otevřete místní nabídku pro zdrojové soubory a pak zvolte Přidat>novou položku.
V dialogovém okně Přidat novou položku vyberte soubor C++ (.cpp), do pole Název zadejte MatrixMultiply.cpp a pak zvolte tlačítko Přidat.
Násobení bez provazování
V této části zvažte násobení dvou matic A a B, které jsou definovány takto:
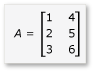

A je matice 3 po 2 a B je matice 2 po 3. Součin násobení A násobením B je následující matice 3:3. Součin se vypočítá vynásobením řádků A sloupci prvku B elementem.

Násobení bez použití C++ AMP
Otevřete MatrixMultiply.cpp a pomocí následujícího kódu nahraďte stávající kód.
#include <iostream> void MultiplyWithOutAMP() { int aMatrix[3][2] = {{1, 4}, {2, 5}, {3, 6}}; int bMatrix[2][3] = {{7, 8, 9}, {10, 11, 12}}; int product[3][3] = {{0, 0, 0}, {0, 0, 0}, {0, 0, 0}}; for (int row = 0; row < 3; row++) { for (int col = 0; col < 3; col++) { // Multiply the row of A by the column of B to get the row, column of product. for (int inner = 0; inner < 2; inner++) { product[row][col] += aMatrix[row][inner] * bMatrix[inner][col]; } std::cout << product[row][col] << " "; } std::cout << "\n"; } } int main() { MultiplyWithOutAMP(); getchar(); }Algoritmus je jednoduchá implementace definice násobení matice. K omezení výpočetní doby nepoužívá žádné paralelní algoritmy ani algoritmy s vlákny.
Na řádku nabídek zvolte Soubor>uložit vše.
Zvolte klávesovou zkratku F5 a spusťte ladění a ověřte, že je výstup správný.
Pokud chcete aplikaci ukončit, zvolte Enter .
Vynásobení pomocí C++ AMP
Do MatrixMultiply.cpp přidejte před metodu
mainnásledující kód.void MultiplyWithAMP() { int aMatrix[] = { 1, 4, 2, 5, 3, 6 }; int bMatrix[] = { 7, 8, 9, 10, 11, 12 }; int productMatrix[] = { 0, 0, 0, 0, 0, 0, 0, 0, 0 }; array_view<int, 2> a(3, 2, aMatrix); array_view<int, 2> b(2, 3, bMatrix); array_view<int, 2> product(3, 3, productMatrix); parallel_for_each(product.extent, [=] (index<2> idx) restrict(amp) { int row = idx[0]; int col = idx[1]; for (int inner = 0; inner <2; inner++) { product[idx] += a(row, inner)* b(inner, col); } }); product.synchronize(); for (int row = 0; row <3; row++) { for (int col = 0; col <3; col++) { //std::cout << productMatrix[row*3 + col] << " "; std::cout << product(row, col) << " "; } std::cout << "\n"; } }Tento kód AMP se podobá kódu bez amp;. Volání spustí
parallel_for_eachjedno vlákno pro každý prvek vproduct.extenta nahradíforsmyčky pro řádek a sloupec. Hodnota buňky na řádku a sloupci je k dispozici vidxsouboru . K prvkům objektuarray_viewmůžete přistupovat buď pomocí[]operátoru a proměnné indexu(), nebo pomocí operátoru a proměnných řádků a sloupců. Příklad ukazuje obě metody. Metodaarray_view::synchronizezkopíruje hodnotyproductproměnné zpět doproductMatrixproměnné.Do horní části MatrixMultiply.cpp přidejte následující
includepříkazy ausingpříkazy.#include <amp.h> using namespace concurrency;Upravte metodu
maintak, aby volala metoduMultiplyWithAMP.int main() { MultiplyWithOutAMP(); MultiplyWithAMP(); getchar(); }Stisknutím klávesové zkratky Ctrl+F5 spusťte ladění a ověřte, že je výstup správný.
Stisknutím mezerníku aplikaci ukončete.
Násobení pomocí provazování
Svázání je technika, ve které rozdělujete data na podmnožiny stejné velikosti, které se označují jako dlaždice. Tři věci se mění, když používáte dlaždici.
Můžete vytvářet
tile_staticproměnné. Přístup k datům vtile_staticprostoru může být mnohokrát rychlejší než přístup k datům v globálním prostoru. Pro každou dlaždici se vytvoří instancetile_staticproměnné a všechna vlákna na dlaždici mají přístup k proměnné. Hlavní výhodou svázání je zvýšení výkonu z důvodutile_staticpřístupu.Můžete volat metodu tile_barrier::wait , která zastaví všechna vlákna v jedné dlaždici na zadaném řádku kódu. Nemůžete zaručit pořadí, ve které budou vlákna spuštěna, pouze to, že všechna vlákna v jedné dlaždici se zastaví při volání
tile_barrier::waitpřed pokračováním v provádění.Máte přístup k indexu vlákna vzhledem k celému
array_viewobjektu a indexu vzhledem k dlaždici. Pomocí místního indexu můžete usnadnit čtení a ladění kódu.
Pokud chcete využít výhod provazování v násobení matice, musí algoritmus rozdělit matici na dlaždice a potom data dlaždic zkopírovat do tile_static proměnných, aby byl rychlejší přístup. V tomto příkladu je matice rozdělena na podmatrice se stejnou velikostí. Součin se najde vynásobením podmatrik. Dva matice a jejich produkt v tomto příkladu jsou:
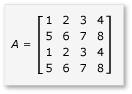
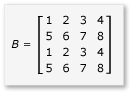
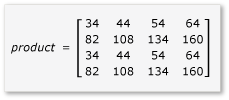
Matice jsou rozdělené na čtyři matice 2x2, které jsou definovány takto:


Součin A a B lze nyní zapsat a vypočítat následujícím způsobem:

Vzhledem k tomu, že matice a až h jsou 2x2 matice, jsou všechny produkty a součty také 2x2 matice. Dále vyplývá, že součin A a B je 4x4 matice podle očekávání. Pokud chcete rychle zkontrolovat algoritmus, vypočítejte hodnotu prvku v prvním řádku, první sloupec v produktu. V příkladu by to byla hodnota prvku v prvním řádku a prvním sloupci ae + bg. Musíte vypočítat pouze první sloupec, první řádek ae a bg pro každý termín. Tato hodnota je ae (1 * 1) + (2 * 5) = 11. Hodnota je bg (3 * 1) + (4 * 5) = 23. Konečná hodnota je 11 + 23 = 34, což je správná.
Pokud chcete tento algoritmus implementovat, kód:
Používá objekt
tiled_extentmístoextentobjektuparallel_for_eachve volání.Používá objekt
tiled_indexmístoindexobjektuparallel_for_eachve volání.Vytvoří
tile_staticproměnné, které budou obsahovat podmatrice.tile_barrier::waitPomocí metody zastaví vlákna pro výpočet produktů podmatric.
Vynásobení pomocí amp; tilingu
Do MatrixMultiply.cpp přidejte před metodu
mainnásledující kód.void MultiplyWithTiling() { // The tile size is 2. static const int TS = 2; // The raw data. int aMatrix[] = { 1, 2, 3, 4, 5, 6, 7, 8, 1, 2, 3, 4, 5, 6, 7, 8 }; int bMatrix[] = { 1, 2, 3, 4, 5, 6, 7, 8, 1, 2, 3, 4, 5, 6, 7, 8 }; int productMatrix[] = { 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 }; // Create the array_view objects. array_view<int, 2> a(4, 4, aMatrix); array_view<int, 2> b(4, 4, bMatrix); array_view<int, 2> product(4, 4, productMatrix); // Call parallel_for_each by using 2x2 tiles. parallel_for_each(product.extent.tile<TS, TS>(), [=] (tiled_index<TS, TS> t_idx) restrict(amp) { // Get the location of the thread relative to the tile (row, col) // and the entire array_view (rowGlobal, colGlobal). int row = t_idx.local[0]; int col = t_idx.local[1]; int rowGlobal = t_idx.global[0]; int colGlobal = t_idx.global[1]; int sum = 0; // Given a 4x4 matrix and a 2x2 tile size, this loop executes twice for each thread. // For the first tile and the first loop, it copies a into locA and e into locB. // For the first tile and the second loop, it copies b into locA and g into locB. for (int i = 0; i < 4; i += TS) { tile_static int locA[TS][TS]; tile_static int locB[TS][TS]; locA[row][col] = a(rowGlobal, col + i); locB[row][col] = b(row + i, colGlobal); // The threads in the tile all wait here until locA and locB are filled. t_idx.barrier.wait(); // Return the product for the thread. The sum is retained across // both iterations of the loop, in effect adding the two products // together, for example, a*e. for (int k = 0; k < TS; k++) { sum += locA[row][k] * locB[k][col]; } // All threads must wait until the sums are calculated. If any threads // moved ahead, the values in locA and locB would change. t_idx.barrier.wait(); // Now go on to the next iteration of the loop. } // After both iterations of the loop, copy the sum to the product variable by using the global location. product[t_idx.global] = sum; }); // Copy the contents of product back to the productMatrix variable. product.synchronize(); for (int row = 0; row <4; row++) { for (int col = 0; col <4; col++) { // The results are available from both the product and productMatrix variables. //std::cout << productMatrix[row*3 + col] << " "; std::cout << product(row, col) << " "; } std::cout << "\n"; } }Tento příklad se výrazně liší od příkladu bez provazování. Kód používá tyto koncepční kroky:
Zkopírujte prvky dlaždice[0,0] z
alocA. Zkopírujte prvky dlaždice[0,0] zblocB. Všimněte si, žeproductje dlaždice, neaab. Proto používáte globální indexy pro přístupa, baproduct. Volánítile_barrier::waitje nezbytné. Zastaví všechna vlákna na dlaždici, dokud se nezaplní obělocAvláknalocB.Vynásobte
locAalocBvložte výsledky doproduct.Zkopírujte prvky dlaždice[0;1]
adolocA. Zkopírujte prvky dlaždice [1,0]bdolocB.Vynásobte
locAje alocBpřidejte je k výsledkům, které jsou již vproduct.Násobení dlaždice [0,0] je dokončeno.
Opakujte pro ostatní čtyři dlaždice. Pro dlaždice neexistuje žádné indexování a vlákna se můžou spouštět v libovolném pořadí. Při každém spuštění
tile_staticvlákna se proměnné vytvoří pro každou dlaždici odpovídajícím způsobem a volání protile_barrier::waitřízení toku programu.Při bližším prozkoumání algoritmu si všimněte, že se každý podmatrix načte do
tile_staticpaměti dvakrát. Přenos dat nějakou dobu trvá. Jakmile jsou ale data vtile_staticpaměti, je přístup k datům mnohem rychlejší. Vzhledem k tomu, že výpočet produktů vyžaduje opakovaný přístup k hodnotám v podmatricích, existuje celkový nárůst výkonu. Pro každý algoritmus se k nalezení optimální velikosti algoritmu a dlaždice vyžaduje experimentování.
V příkladech jiných než AMP a jiných než dlaždic se ke každému prvku A a B přistupuje čtyřikrát z globální paměti k výpočtu produktu. V příkladu dlaždice se ke každému prvku přistupuje dvakrát z globální paměti a čtyřikrát z
tile_staticpaměti. To není významné zvýšení výkonu. Pokud by však matice A a B byly 1024 × 1024 a velikost dlaždice byla 16, došlo by k významnému zvýšení výkonu. V takovém případě by se každý prvek zkopíroval dotile_staticpaměti pouze 16krát a přistupoval ztile_staticpaměti 1024krát.Upravte hlavní metodu tak, aby volala metodu
MultiplyWithTiling, jak je znázorněno.int main() { MultiplyWithOutAMP(); MultiplyWithAMP(); MultiplyWithTiling(); getchar(); }Stisknutím klávesové zkratky Ctrl+F5 spusťte ladění a ověřte, že je výstup správný.
Stisknutím mezerníku aplikaci ukončete.
Viz také
C++ AMP (C++ Accelerated Massive Parallelism)
Návod: Ladění aplikace C++ AMP