Auswerten der Ergebnisse von Experimenten des automatisierten maschinellen Lernens
In diesem Artikel erfahren Sie, wie Sie Modelle, die durch Ihr Experiment für automatisiertes maschinelles Lernen (automatisiertes ML) trainiert wurden, bewerten und vergleichen können. Im Verlauf eines automatisierten ML-Experiments werden viele Ausführungen erstellt und jede Ausführung erstellt ein Modell. Für jedes Modell generiert das automatisierte maschinelle Lernen Auswertungsmetriken und Diagramme, mit denen Sie die Leistung des Modells messen können. Generieren Sie ein verantwortungsvolles KI-Dashboard, um eine ganzheitliche Bewertung und das Debuggen des empfohlenen besten Modells durchzuführen. Dies umfasst Erkenntnisse wie Modellerklärungen, Fairness- und Leistungs-Explorer, Daten-Explorer und Modellfehleranalyse. Erfahren Sie mehr darüber, wie Sie ein verantwortungsvolles KI-Dashboard generieren können.
Das automatisierte maschinelle Lernen generiert z. B. die folgenden Diagramme basierend auf dem Experimenttyp.
Wichtig
Die in diesem Artikel markierten Elemente (Vorschau) sind aktuell als öffentliche Vorschau verfügbar. Die Vorschauversion wird ohne Vereinbarung zum Servicelevel bereitgestellt und ist nicht für Produktionsworkloads vorgesehen. Manche Features werden möglicherweise nicht unterstützt oder sind nur eingeschränkt verwendbar. Weitere Informationen finden Sie unter Zusätzliche Nutzungsbestimmungen für Microsoft Azure-Vorschauen.
Voraussetzungen
- Ein Azure-Abonnement. (Sollten Sie über kein Azure-Abonnement verfügen, können Sie ein kostenloses Konto erstellen, bevor Sie beginnen.)
- Ein Azure Machine Learning-Experiment, das erstellt wurde mit einer der folgenden Optionen:
- Azure Machine Learning Studio (kein Code erforderlich)
- Python-SDK für Azure Machine Learning
Auftragsergebnisse anzeigen
Nachdem Ihr Experiment mit automatisiertem maschinellem Lernen abgeschlossen ist, können Sie einen Verlauf der Ausführungen über Folgendes finden:
- Browser mit Azure Machine Learning Studio
- Ein Jupyter Notebook mithilfe des JobDetails Jupyter-Widgets
Die folgenden Schritte und das Video zeigen Ihnen, wie Sie den Ausführungsverlauf sowie die Metriken und Diagramme der Modellauswertung im Studio anzeigen:
- Melden Sie sich beim Studio an, und navigieren Sie zu Ihrem Arbeitsbereich.
- Wählen Sie im Menü auf der linken Seite die Option Aufträge aus.
- Wählen Sie Ihr Experiment aus der Liste der Experimente aus.
- Wählen Sie in der Tabelle unten auf der Seite eine automatisierte ML-Ausführung aus.
- Wählen Sie auf der Registerkarte Modelle den Algorithmusnamen für das Modell aus, das Sie auswerten möchten.
- Verwenden Sie auf der Registerkarte Metriken die Kontrollkästchen auf der linken Seite, um Metriken und Diagramme anzuzeigen.
Klassifizierungsmetrik
Automatisiertes maschinelles Lernen berechnet Leistungsmetriken für jedes Klassifizierungsmodell, das für Ihr Experiment erstellt wurde. Diese Metriken basieren auf der scikit learn-Implementierung.
Viele Klassifizierungsmetriken sind für die binäre Klassifizierung von zwei Klassen definiert und erfordern eine Mittelwerterstellung über die Klassen, um einen Score für die mehrklassige Klassifizierung zu erhalten. Scikit-learn bietet mehrere Methoden zur Mittelwerterstellung, von denen drei über das automatisierte maschinelle Lernen bereitgestellt werden: macro, micro und weighted.
- Macro: Berechnet die Metrik für jede Klasse und bildet den ungewichteten Mittelwert.
- Micro: Berechnet die Metrik global, indem die gesamten True Positive-, False Negative- und False Positive-Ergebnisse gezählt werden (unabhängig von den Klassen).
- Weighted: Berechnet die Metrik für jede Klasse und bildet den gewichteten Mittelwert basierend auf der Anzahl der Stichproben pro Klasse.
Während jede Methode zur Mittelwerterstellung ihre Vorteile hat, ist eine gemeinsame Überlegung bei der Auswahl der geeigneten Methode das Klassenungleichgewicht. Wenn Klassen eine unterschiedliche Anzahl von Stichproben aufweisen, kann es informativer sein, einen Macro-Mittelwert zu verwenden, bei dem Minderheitsklassen die gleiche Gewichtung wie Mehrheitsklassen erhalten. Weitere Informationen finden Sie unter Gegenüberstellung von Binär- und Multiklassenmetriken beim automatisierten maschinellen Lernen.
In der folgenden Tabelle sind die Modellleistungsmetriken zusammengefasst, die automatisiertes ML für jedes Klassifizierungsmodell berechnet, das für Ihr Experiment generiert wird. Weitere Details finden Sie in der scikit-learn-Dokumentation, die im Feld Berechnung der jeweiligen Metrik verlinkt ist.
Hinweis
Weitere Informationen zu Metriken für Bildklassifizierungsmodelle finden Sie im Abschnitt Bildmetriken.
| Metric | BESCHREIBUNG | Berechnung |
|---|---|---|
| AUC | AUC ist die Fläche unter der ROC-Kurve (Receiver Operating Characteristic Curve). Ziel: Je näher an 1 desto besser Bereich: [0, 1] Zu den unterstützten Metriknamen gehören AUC_macro, das arithmetische Mittel der AUC für jede Klasse.AUC_micro: wird durch Zählen aller True Positive-, False Negative- und False Positive-Ergebnisse berechnet. AUC_weighted, das arithmetische Mittel des Ergebnisses für jede Klasse, gewichtet gemäß der Anzahl der TRUE-Instanzen in jeder Klasse. AUC_binary, der Wert von AUC, indem eine bestimmte Klasse als true-Klasse behandelt wird und alle anderen Klassen als false-Klasse kombiniert werden. |
Berechnung |
| accuracy | Die Genauigkeit ist der Anteil der Vorhersagen, die genau mit den wahren Klassenbezeichnungen übereinstimmen. Ziel: Je näher an 1 desto besser Bereich: [0, 1] |
Berechnung |
| average_precision | Die durchschnittliche Genauigkeit fasst eine Precision-Recall-Kurve als gewichteten Mittelwert der bei jedem Schwellenwert erzielten Genauigkeiten zusammen, wobei die Zunahme beim Recall aus dem vorherigen Schwellenwert als Gewichtung verwendet wird. Ziel: Je näher an 1 desto besser Bereich: [0, 1] Zu den unterstützten Metriknamen gehören average_precision_score_macro, das arithmetische Mittel des durchschnittlichen Genauigkeitswerts jeder Klasse.average_precision_score_micro: wird durch Zählen aller True Positive-, False Negative- und False Positive-Ergebnisse berechnet.average_precision_score_weighted, das arithmetische Mittel der durchschnittlichen Genauigkeit für jede Klasse, gewichtet gemäß der Anzahl der TRUE-Instanzen in jeder Klasse. average_precision_score_binary, der Wert der durchschnittlichen Genauigkeit, indem eine bestimmte Klasse als true-Klasse behandelt wird und alle anderen Klassen als false-Klasse kombiniert werden. |
Berechnung |
| balanced_accuracy | „Balanced accuracy“ ist das arithmetische Mittel des Recalls für jede Klasse. Ziel: Je näher an 1 desto besser Bereich: [0, 1] |
Berechnung |
| f1_score | „F1 score“ ist das harmonische Mittel aus Genauigkeit und Recall. Es handelt sich um ein ausgewogenes Maß sowohl für False-Positive- als auch False-Negative-Ergebnisse. True-Negative-Ergebnisse werden dabei jedoch nicht berücksichtigt. Ziel: Je näher an 1 desto besser Bereich: [0, 1] Zu den unterstützten Metriknamen gehören f1_score_macro: Das arithmetische Mittel des F1-Ergebnisses für jede Klasse. f1_score_micro: Wird global durch Zählen der insgesamt True Positive-, False Negative- und False Positive-Ergebnisse berechnet. f1_score_weighted: Gewichteter Mittelwert nach Klassenhäufigkeit des F1-Ergebnisses für jede Klasse. f1_score_binary, der Wert von f1, indem eine bestimmte Klasse als true-Klasse behandelt wird und alle anderen Klassen als false-Klasse kombiniert werden. |
Berechnung |
| log_loss | Dies ist die Verlustfunktion, die bei der (multinomialen) logistischen Regression und deren Erweiterungen wie z. B. neuronalen Netzen verwendet wird. Sie ist definiert als die negative Log-Wahrscheinlichkeit der True-Bezeichnungen bei den Vorhersagen eines probabilistischen Klassifizierers. Ziel: Je näher an 0 desto besser Bereich: [0, inf) |
Berechnung |
| norm_macro_recall | Der normalisierte Makro-Recall wird über das Recall-Makro gemittelt und normalisiert, damit die zufällige Leistung ein Ergebnis von 0 und die ideale Leistung einen Wert von 1 liefert. Ziel: Je näher an 1 desto besser Bereich: [0, 1] |
(recall_score_macro - R) / (1 - R) wobei R der erwartete Wert von recall_score_macro für zufällige Vorhersagen ist.R = 0.5 zur binären Klassifizierung. R = (1 / C) für C-Klassen-Klassifizierungsprobleme. |
| matthews_correlation | Der Matthews-Korrelationskoeffizient ist ein ausgewogenes Maß für die Genauigkeit, das auch dann verwendet werden kann, wenn eine Klasse viel mehr Stichproben als eine andere aufweist. Ein Koeffizient von 1 bedeutet perfekte Vorhersage, 0 zufällige Vorhersage und -1 inverse Vorhersage. Ziel: Je näher an 1 desto besser Bereich: [-1, 1] |
Berechnung |
| precision (Genauigkeit) | Genauigkeit ist die Fähigkeit eines Modells, negative Stichproben nicht als positiv zu bezeichnen. Ziel: Je näher an 1 desto besser Bereich: [0, 1] Zu den unterstützten Metriknamen gehören precision_score_macro, das arithmetische Mittel der Genauigkeit für jede Klasse. precision_score_micro, wird global durch Zählen der insgesamt True Positive- und False Positive-Ergebnisse berechnet. precision_score_weighted, das arithmetische Mittel der Genauigkeit für jede Klasse, gewichtet gemäß der Anzahl der TRUE-Instanzen in jeder Klasse. precision_score_binary, der Wert der Genauigkeit, indem eine bestimmte Klasse als true-Klasse behandelt wird und alle anderen Klassen als false-Klasse kombiniert werden. |
Berechnung |
| recall (Abruf) | Recall (Abruf) ist die Fähigkeit eines Modells, alle positiven Stichproben zu erkennen. Ziel: Je näher an 1 desto besser Bereich: [0, 1] Zu den unterstützten Metriknamen gehören recall_score_macro: Das arithmetische Mittel des Recalls für jede Klasse. recall_score_micro: Dies wird global durch das Zählen der True-Positive-, False-Negative- und False-Positive-Ergebnisse insgesamt berechnet.recall_score_weighted: Das arithmetische Mittel des Recalls für jede Klasse, gewichtet gemäß der Anzahl der TRUE-Instanzen in jeder Klasse. recall_score_binary, der Wert des Abrufs, indem eine bestimmte Klasse als true-Klasse behandelt wird und alle anderen Klassen als false-Klasse kombiniert werden. |
Berechnung |
| weighted_accuracy | Die gewichtete Genauigkeit ist eine Genauigkeit, bei der jede Stichprobe mit der Gesamtzahl der Stichproben, die zur gleichen Klasse gehören, gewichtet wird. Ziel: Je näher an 1 desto besser Bereich: [0, 1] |
Berechnung |
Gegenüberstellung von Binär- und Multiklassenmetriken für die Klassifizierung
Das automatisierte maschinelle Lernen erkennt automatisch, ob die Daten binär sind, und ermöglicht Benutzern auch das Aktivieren binärer Klassifizierungsmetriken, auch wenn es sich um Multiklassen-Daten handelt, indem eine true-Klasse angegeben wird. Multiklassen-Klassifizierungsmetriken werden gemeldet, wenn ein Dataset über mindestens zwei Klassen verfügt. Binäre Klassifizierungsmetriken werden nur gemeldet, wenn es sich um binäre Daten handelt.
Beachten Sie, dass Multiklassen-Klassifizierungsmetriken für die Multiklassen-Klassifizierung vorgesehen sind. Wenn eine solche Metrik auf ein binäres Dataset angewendet wird, wird keine Klasse von den Metriken, wie vielleicht erwartet, als true behandelt. Metriken, die eindeutig für mehrere Klassen vorgesehen sind, sind mit dem Suffix micro, macrooder weighted gekennzeichnet. Beispiele hierfür sind etwa average_precision_score, f1_score, precision_score, recall_score und AUC. Anstatt beispielsweise den Abruf als tp / (tp + fn) zu berechnen, wird beim Durchschnittsabruf mit mehreren Klassen (micro, macro oder weighted) für beide Klassen eines Datasets mit Binärklassifizierung ein Durchschnitt gebildet. Dies entspricht der separaten Berechnung des Abrufs für die Klassen true und false und der anschließenden Bildung des Durchschnitts der beiden Klassen.
Obwohl die automatische Erkennung der Binärklassifizierung unterstützt wird, wird weiterhin empfohlen, die true-Klasse immer manuell anzugeben, um sicherzustellen, dass die Binärklassifizierungsmetriken für die richtige Klasse berechnet werden.
Um Metriken für Binärklassifizierungsdatasets zu aktivieren, wenn es sich um ein Multiklassendataset handelt, müssen Benutzer nur die Klasse angeben, die als true-Klasse behandelt werden soll, und diese Metriken werden dann berechnet.
Konfusionsmatrix
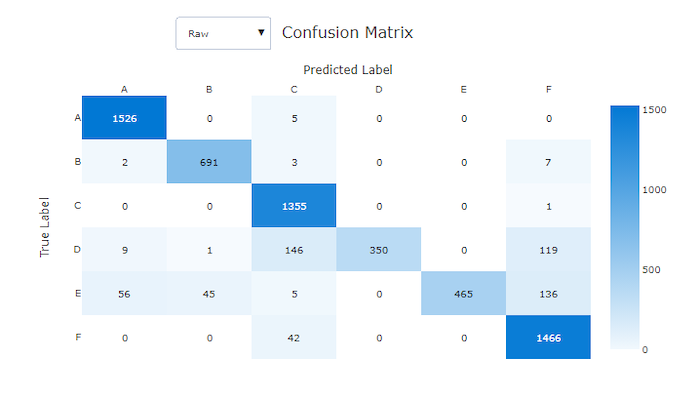
Konfusionsmatrizen bieten eine visuelle Darstellung dafür, wie ein Machine Learning-Modell systematische Fehler in seinen Vorhersagen für Klassifikationsmodelle macht. Das Wort „Konfusion“ im Namen stammt von einem Modell, das Stichproben „verwechselt“ oder falsch bezeichnet. Eine Zelle in Zeile i und Spalte j in einer Konfusionsmatrix enthält die Anzahl der Stichproben im Auswertungsdataset, die zur Klasse C_i gehören und vom Modell als Klasse C_j klassifiziert wurden.
Im Studio zeigt eine dunklere Zelle eine höhere Anzahl von Stichproben an. Durch Auswahl der Ansicht Normalisiert in der Dropdownliste wird jede Matrixzeile normalisiert, um den Prozentsatz der Klasse C_i anzuzeigen, der als Klasse C_j vorhergesagt wird. Der Vorteil der Standardansicht der Rohdaten ist, dass Sie sehen können, ob ein Ungleichgewicht in der Verteilung der tatsächlichen Klassen dazu geführt hat, dass das Modell Stichproben aus der Minderheitsklasse falsch klassifiziert hat, wobei es sich um ein häufiges Problem in unausgeglichenen Datasets handelt.
Die Konfusionsmatrix eines guten Modells wird die meisten Stichproben entlang der Diagonalen aufweisen.
Konfusionsmatrix für ein gutes Modell

Konfusionsmatrix für ein ungültiges Modell
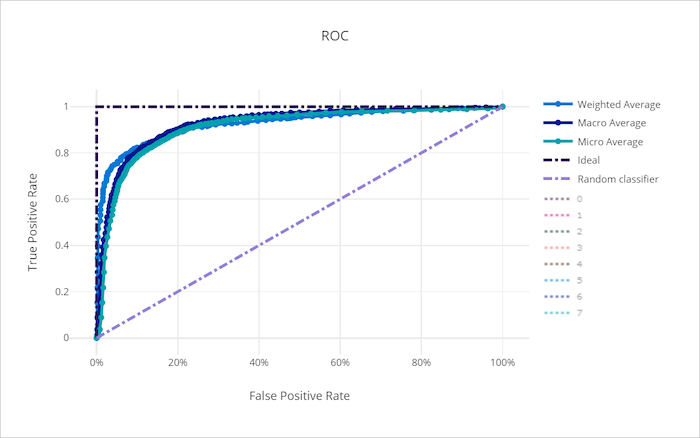
ROC-Kurve
Die ROC-Kurve (Receiver Operating Characteristic) stellt das Verhältnis zwischen der True Positive- (TPR) und der False Positive-Rate (FPR) dar, wenn sich der Entscheidungsschwellenwert ändert. Die ROC-Kurve kann weniger aussagekräftig sein, wenn Modelle auf der Grundlage von Datasets mit stark unausgeglichenen Klassen trainiert werden, da die Beiträge von Minderheitsklassen ggf. durch die Mehrheitsklasse verdrängt wird.
Der Bereich unter der Kurve (AUC) kann als der Anteil der richtig klassifizierten Stichproben interpretiert werden. Genauer gesagt, ist der AUC die Wahrscheinlichkeit, dass der Klassifizierer eine zufällig ausgewählte positive Stichprobe höher einstuft als eine zufällig ausgewählte negative Stichprobe. Die Form der Kurve gibt eine Vorstellung von der Beziehung zwischen TPR und FPR in Abhängigkeit vom Klassifizierungsschwellenwert oder der Entscheidungsgrenze.
Eine Kurve, die sich der oberen linken Ecke des Diagramms nähert, nähert sich einer TPR von 100 % und FPR von 0 %, dem bestmöglichen Modell. Ein zufälliges Modell würde eine ROC-Kurve entlang der y = x-Linie von der linken unteren Ecke bis zur rechten oberen Ecke erzeugen. Ein Modell, das schlechter als ein zufälliges Modell ist, würde eine ROC-Kurve aufweisen, die unter die y = x-Linie eintaucht.
Tipp
Für Klassifizierungsexperimente kann jedes der Liniendiagramme, die für automatisierte ML-Modelle erstellt werden, verwendet werden, um das Modell pro Klasse oder gemittelt über alle Klassen auszuwerten. Sie können zwischen diesen verschiedenen Ansichten umschalten, indem Sie auf die Klassenbezeichnungen in der Legende auf der rechten Seite des Diagramms klicken.
ROC-Kurve für ein gutes Modell

ROC-Kurve für ein ungültiges Modell
Kurve zu Genauigkeit/Abruf
Die Kurve zu Genauigkeit/Abruf stellt das Verhältnis zwischen Genauigkeit und Abruf bei Änderung des Entscheidungsschwellwerts dar. Abruf ist die Fähigkeit eines Modells, alle positiven Stichproben zu erkennen und Genauigkeit ist die Fähigkeit eines Modells, negative Stichproben nicht als positiv zu bezeichnen. Einige geschäftliche Probleme erfordern möglicherweise einen höheren Abruf und andere eine höhere Genauigkeit, abhängig von der relativen Wichtigkeit der Vermeidung von False Negative- gegenüber False Positive-Ergebnissen.
Tipp
Für Klassifizierungsexperimente kann jedes der Liniendiagramme, die für automatisierte ML-Modelle erstellt werden, verwendet werden, um das Modell pro Klasse oder gemittelt über alle Klassen auszuwerten. Sie können zwischen diesen verschiedenen Ansichten umschalten, indem Sie auf die Klassenbezeichnungen in der Legende auf der rechten Seite des Diagramms klicken.
Kurve zu Genauigkeit/Abruf für ein gutes Modell
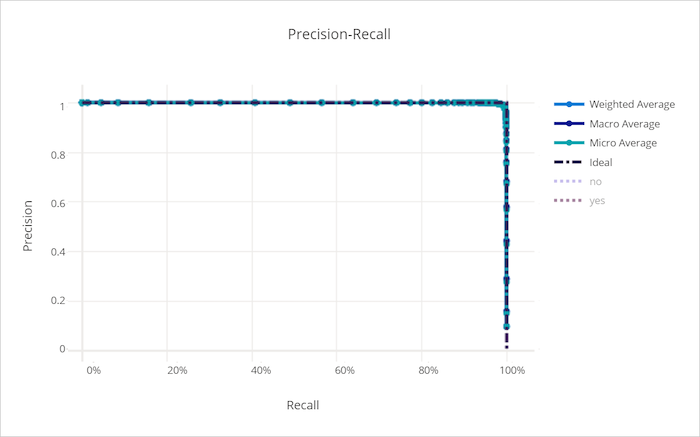
Kurve zu Genauigkeit/Abruf für ein ungültiges Modell
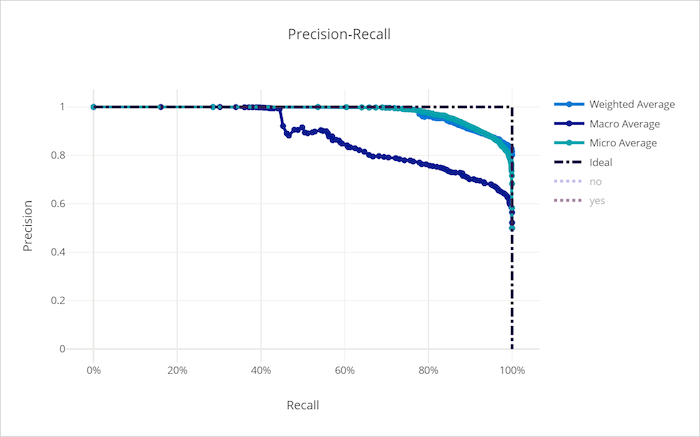
Kumulierte Gewinnkurve
Die kumulative Gewinnkurve stellt den Prozentsatz der richtig klassifizierten positiven Stichproben als Funktion des Prozentsatzes der betrachteten Stichproben dar, wobei wir die Stichproben in der Reihenfolge der vorhergesagten Wahrscheinlichkeit betrachten.
Um den Gewinn zu berechnen, sortieren Sie zunächst alle Stichproben von der höchsten zur niedrigsten vom Modell vorhergesagten Wahrscheinlichkeit. Nehmen Sie dann x% der höchstmöglichen Vorhersagen. Teilen Sie die Anzahl der in diesem x% erkannten positiven Stichproben durch die Gesamtzahl der positiven Stichproben, um den Gewinn zu erhalten. Der kumulative Gewinn ist der Prozentsatz an positiven Stichproben, die wir erkennen, wenn wir einen gewissen Prozentsatz der Daten berücksichtigen, der mit hoher Wahrscheinlichkeit zur positiven Klasse gehört.
Ein perfektes Modell wird alle positiven Stichproben über alle negativen Stichproben stellen, was eine kumulative Gewinnkurve ergibt, die aus zwei geraden Segmenten besteht. Die erste ist eine Linie mit der Steigung 1 / x von (0, 0) bis (x, 1), wobei x der Anteil der Stichproben ist, die zur positiven Klasse gehören (1 / num_classes, wenn die Klassen ausgeglichen sind). Die zweite ist eine horizontale Linie von (x, 1) bis (1, 1). Im ersten Segment werden alle positiven Stichproben richtig klassifiziert und der kumulative Gewinn wechselt innerhalb der ersten x% der betrachteten Stichproben zu 100%.
Das Baseline-Zufallsmodell hat eine kumulative Gewinnkurve, die y = x folgt, wobei für x% der betrachteten Stichproben nur etwa x% der gesamten positiven Stichproben erkannt wurden. Ein perfektes Modell für ein ausgeglichenes Dataset verfügt über eine Mikro-Mittelwertkurve und eine Makro-Mittelwertkurve mit der Steigung num_classes, bis der kumulative Gewinn 100 % beträgt. Anschließend verläuft er horizontal, bis der Datenprozentwert 100 entspricht.
Tipp
Für Klassifizierungsexperimente kann jedes der Liniendiagramme, die für automatisierte ML-Modelle erstellt werden, verwendet werden, um das Modell pro Klasse oder gemittelt über alle Klassen auszuwerten. Sie können zwischen diesen verschiedenen Ansichten umschalten, indem Sie auf die Klassenbezeichnungen in der Legende auf der rechten Seite des Diagramms klicken.
Kumulative Gewinnkurve für ein gutes Modell

Kumulative Gewinnkurve für ein ungültiges Modell

Prognosegütekurve
Die Prognosegütekurve zeigt, wie viel besser ein Modell im Vergleich zu einem Zufallsmodell abschneidet. Prognosegüte ist definiert als das Verhältnis des kumulativen Gewinns zum kumulativen Gewinn eines Zufallsmodells (die immer 1 sein sollte).
Diese relative Leistungsangabe berücksichtigt, dass die Klassifizierung mit zunehmender Klassenanzahl schwieriger wird. (Ein Zufallsmodell sagt bei einem Dataset mit zehn Klassen einen höheren Anteil von Stichproben falsch vorher als bei einem Dataset mit zwei Klassen.)
Die Baseline-Prognosegütekurve ist die y = 1-Linie, bei der die Modellleistung mit der eines Zufallsmodells übereinstimmt. Im Allgemeinen wird die Prognosegütekurve für ein gutes Modell in diesem Diagramm höher und weiter von der X-Achse entfernt sein, was zeigt, dass das Modell um ein Vielfaches besser abschneidet als bloßes Raten, wenn es in seinen Vorhersagen am zuversichtlichsten ist.
Tipp
Für Klassifizierungsexperimente kann jedes der Liniendiagramme, die für automatisierte ML-Modelle erstellt werden, verwendet werden, um das Modell pro Klasse oder gemittelt über alle Klassen auszuwerten. Sie können zwischen diesen verschiedenen Ansichten umschalten, indem Sie auf die Klassenbezeichnungen in der Legende auf der rechten Seite des Diagramms klicken.
Prognosegütekurve für ein gutes Modell

Prognosegütekurve für ein ungültiges Modell

Kalibrierungskurve
Die Kalibrierungskurve stellt die Konfidenz eines Modells in Bezug auf seine Vorhersagen im Vergleich zum Anteil positiver Stichproben auf den jeweiligen Konfidenzebenen dar. Ein gut kalibriertes Modell wird 100 % der Vorhersagen richtig klassifizieren, denen es eine Konfidenz von 100 % zuweist, 50 % der Vorhersagen, denen es eine Konfidenz von 50 % zuweist, 20 % der Vorhersagen, denen es eine Konfidenz von 20 % zuweist usw. Ein perfekt kalibriertes Modell hat eine Kalibrierungskurve, die der y = x-Linie folgt, in der das Modell die Wahrscheinlichkeit perfekt vorhersagt, dass Stichproben zu den einzelnen Klassen gehören.
Bei einem Modell mit übermäßiger Konfidenz werden Wahrscheinlichkeiten übermäßig nah bei 0 bzw. 1 vorhergesagt, sodass hinsichtlich der Klasse der jeweiligen Stichproben selten eine Unsicherheit besteht, und die Kalibrierungskurve wird ähnlich wie ein rückwärtsgerichtetes „S“ aussehen. Bei einem Modell mit zu geringer Konfidenz wird der vorhergesagten Klasse im Durchschnitt eine geringere Wahrscheinlichkeit zugewiesen, und die zugehörige Kalibrierungskurve wird ähnlich wie ein „S“ aussehen. Die Kalibrierungskurve stellt nicht die Fähigkeit eines Modells zur richtigen Klassifizierung dar, sondern seine Fähigkeit, seinen Vorhersagen die richtige Konfidenz zuzuordnen. Ein ungültiges Modell kann immer noch eine geeignete Kalibrierungskurve aufweisen, wenn das Modell eine geringe Konfidenz und eine hohe Unsicherheit richtig zuweist.
Hinweis
Die Kalibrierungskurve ist hinsichtlich der Anzahl der Stichproben empfindlich, sodass ein kleiner Validierungssatz zu verrauschten Ergebnissen führen kann, die schwer zu interpretieren sein können. Dies bedeutet nicht unbedingt, dass das Modell nicht richtig kalibriert ist.
Kalibrierungskurve für ein gutes Modell
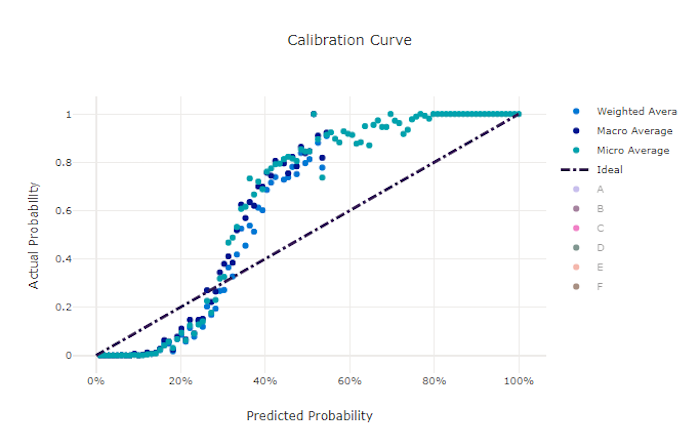
Kalibrierungskurve für ein ungültiges Modell

Regressions-/Vorhersagemetriken
Das automatisierte maschinelle Lernen berechnet dieselben Leistungsmetriken für jedes generierte Modell, unabhängig davon, ob es sich um ein Regressions- oder Vorhersageexperiment handelt. Diese Metriken werden auch normalisiert, um einen Vergleich zwischen Modellen zu ermöglichen, die für Daten mit unterschiedlichen Bereichen trainiert wurden. Weitere Informationen finden Sie unter Metrische Normalisierung.
In der folgenden Tabelle sind die für die Regressions- und Vorhersageexperimente generierten Modellleistungsmetriken zusammengefasst. Wie die Klassifizierungsmetriken basieren auch diese Metriken auf den scikit learn-Implementierungen. Die entsprechende scikit learn-Dokumentation ist entsprechend verlinkt, und zwar im Feld Berechnung.
| Metrik | BESCHREIBUNG | Berechnung |
|---|---|---|
| explained_variance | Die erläuterte Varianz misst das Ausmaß, in dem ein Modell die Variation in der Zielvariablen erläutert. Hierbei handelt es sich um den prozentualen Rückgang der Varianz der ursprünglichen Daten im Vergleich zur Varianz der Fehler. Wenn der Mittelwert der Fehler 0 beträgt, entspricht er dem Bestimmungskoeffizienten (siehe „r2_score“ im folgenden Diagramm). Ziel: Je näher an 1 desto besser Bereich: (-inf, 1] |
Berechnung |
| mean_absolute_error | Der mittlere absolute Fehler ist der erwartete Wert des absoluten Differenzwerts zwischen dem Ziel und der Vorhersage. Ziel: Je näher an 0 desto besser Bereich: [0, inf) Typen: mean_absolute_error normalized_mean_absolute_error, mean_absolute_error (mittlere absolute Abweichung) geteilt durch den Bereich der Daten. |
Berechnung |
| mean_absolute_percentage_error | Der mittlere absolute prozentuale Fehler (Mean Absolute Percentage Error, MAPE) ist ein Maß für die durchschnittliche Differenz zwischen einem vorhergesagten Wert und dem tatsächlichen Wert. Ziel: Je näher an 0 desto besser Bereich: [0, inf) |
|
| median_absolute_error | Der mittlere absolute Fehler ist der Median aller absoluten Differenzen zwischen dem Ziel und der Vorhersage. Dieser Verlust ist stabil in Bezug auf Ausreißer. Ziel: Je näher an 0 desto besser Bereich: [0, inf) Typen: median_absolute_errornormalized_median_absolute_error: median_absolute_error geteilt durch den Bereich der Daten. |
Berechnung |
| r2_score | R2 (der Bestimmungskoeffizient) misst die proportionale Reduzierung der mittleren quadratischen Abweichung (MQA) in Relation zur Gesamtvarianz der betrachteten Daten. Ziel: Je näher an 1 desto besser Bereich: [-1, 1] Hinweis: R2 umfasst häufig den Bereich (-inf, 1]. Da die MQA größer als die beobachtete Varianz sein kann, kann R2 je nach Daten und Modellvorhersagen beliebig große negative Werte haben. Gemeldete R2-Scores werden vom automatisierten maschinellen Lernen auf „-1“ beschnitten, sodass der Wert „-1“ für R2 wahrscheinlich bedeutet, dass der tatsächliche R2-Score kleiner als „-1“ ist. Berücksichtigen Sie die anderen Metrikwerte und die Eigenschaften der Daten, wenn Sie einen negativen R2-Score interpretieren. |
Berechnung |
| root_mean_squared_error | Die Wurzel aus dem mittleren quadratischen Fehler (Root Mean Squared Error, RMSE) ist die Quadratwurzel der erwarteten quadratischen Differenz zwischen dem Ziel und der Vorhersage. Für einen ausgewogenen Schätzer ist der RMSE gleich der Standardabweichung. Ziel: Je näher an 0 desto besser Bereich: [0, inf) Typen: root_mean_squared_error normalized_root_mean_squared_error: root_mean_squared_error geteilt durch den Bereich der Daten. |
Berechnung |
| root_mean_squared_log_error | Die Wurzel aus dem mittleren quadratischen logarithmischen Fehler ist die Quadratwurzel des erwarteten quadratischen logarithmischen Fehlers. Ziel: Je näher an 0 desto besser Bereich: [0, inf) Typen: root_mean_squared_log_error normalized_root_mean_squared_log_error: root_mean_squared_log_error geteilt durch den Bereich der Daten. |
Berechnung |
| spearman_correlation | Die Spearman-Korrelation ist ein nicht parametrisches Maß für die Monotonie der Beziehung zwischen zwei Datasets. Im Gegensatz zur Pearson-Korrelation geht die Spearman-Korrelation nicht davon aus, dass beide Datasets normal verteilt sind. Wie bei anderen Korrelationskoeffizienten variiert Spearman zwischen -1 und 1, wobei 0 für keine Korrelation steht. Korrelationen von -1 oder 1 implizieren eine exakt monotone Beziehung. Bei Spearman handelt es sich um eine Korrelationsmetrik der Rangfolge, was bedeutet, dass Änderungen an vorhergesagten oder tatsächlichen Werten das Spearman-Ergebnis nicht verändern, wenn sie die Rangfolge der vorhergesagten oder tatsächlichen Werte nicht verändern. Ziel: Je näher an 1 desto besser Bereich: [-1, 1] |
Berechnung |
Metrische Normalisierung
Das automatisierte maschinelle Lernen normalisiert Regressions- und Vorhersagemetriken, was den Vergleich zwischen Modellen ermöglicht, die für Daten mit unterschiedlichen Bereichen trainiert wurden. Ein Modell, das für Daten mit einem größeren Bereich trainiert wurde, weist einen höheren Fehlerwert auf als dasselbe Modell, das für Daten mit einem kleineren Bereich trainiert wurde, es sei denn, dieser Fehler wird normalisiert.
Es gibt zwar keine Standardmethode zum Normalisieren von Fehlermetriken, beim automatisierten maschinellen Lernen wird der Fehler jedoch üblicherweise durch den Bereich der Daten geteilt: normalized_error = error / (y_max - y_min).
Hinweis
Der Bereich der Daten wird nicht mit dem Modell gespeichert. Wenn Sie mit dem selben Modell einen Rückschluss für einen Testsatz für zurückgehaltene Daten ziehen, können sich y_min und y_max entsprechend den Testdaten ändern und die normalisierten Metriken möglicherweise nicht direkt verwendet werden, um die Leistung der Modelle für Trainings- und Testsätze zu vergleichen. Sie können den Wert von y_min und y_max aus Ihrem Trainingssatz weitergeben, um den Vergleich fair zu gestalten.
Vorhersagemetriken: Normalisierung und Aggregation
Das Berechnen von Metriken für die Vorhersagemodellauswertung erfordert einige besondere Überlegungen, wenn die Daten mehrere Zeitreihen enthalten. Es gibt zwei natürliche Optionen zum Aggregieren von Metriken mehrerer Reihen:
- Makrodurchschnitt, bei dem die Auswertungsmetriken aus jeder Reihe die gleiche Gewichtung erhalten
- Mikrodurchschnitt, bei dem Auswertungsmetriken für jede Vorhersage die gleiche Gewichtung aufweisen
Diese Fälle sind direkt analog zur Berechnung der Makro- und Mikrodurchschnittswerte bei der Multiklassenklassifizierung.
Die Unterscheidung zwischen Makro- und Mikrodurchschnitt kann bei der Auswahl einer primären Metrik für die Modellauswahl von Bedeutung sein. Betrachten Sie beispielsweise ein Einzelhandelsszenario, in dem Sie die Nachfrage nach einer Auswahl von Consumerprodukten vorhersagen möchten. Einige Produkte werden in viel größeren Mengen verkauft als andere. Wenn Sie eine mittlere quadratische Gesamtabweichung (RMSE) mit Mikro-Mittelwert als primäre Metrik auswählen, ist es möglich, dass die häufig verkauften Artikel einen Großteil des Modellierungsfehlers ausmachen und folglich die Metrik dominieren. Der Modellauswahlalgorithmus kann Modelle bevorzugen, die bei den häufig verkauften Artikeln eine höhere Genauigkeit aufweisen als bei den selten verkauften Artikeln. Im Gegensatz dazu gibt ein normalisierter RMSE mit Makrodurchschnitt selten verkauften Artikeln ungefähr die gleiche Gewichtung wie häufig verkauften Artikeln.
Die folgende Tabelle zeigt, welche Vorhersagemetriken des automatisierten maschinellen Lernens den Makro-Mittelwert bzw. Mikro-Mittelwert verwenden:
| Makrodurchschnitt | Mikrodurchschnitt |
|---|---|
normalized_mean_absolute_error, normalized_median_absolute_error, normalized_root_mean_squared_error, normalized_root_mean_squared_log_error |
mean_absolute_error, median_absolute_error, root_mean_squared_error, root_mean_squared_log_error, r2_score, explained_variance, spearman_correlation, mean_absolute_percentage_error |
Beachten Sie, dass Metriken mit Makrodurchschnitt jede Reihe separat normalisieren. Für die normalisierten Metriken jeder Reihe wird dann der Durchschnittswert berechnet, um das Endergebnis zu erhalten. Die richtige Wahl von Makrodurchschnitt und Mikrodurchschnitt hängt vom Geschäftsszenario ab, aber wir empfehlen im Allgemeinen die Verwendung von normalized_root_mean_squared_error.
Restdaten
Das Restdatendiagramm ist ein Histogramm der Vorhersagefehler (Restdaten), die für Regressions- und Vorhersageexperimente generiert wurden. Die Restdaten werden als y_predicted - y_true für alle Stichproben berechnet und dann als Histogramm angezeigt, um die Modellverzerrung zu zeigen.
In diesem Beispiel ist zu beachten, dass beide Modelle leicht verzerrt sind und einen niedrigeren als den tatsächlichen Wert vorhersagen. Dies ist nicht ungewöhnlich für ein Dataset mit einer ungleichmäßigen Verteilung der tatsächlichen Ziele, weist aber auf eine schlechtere Modellleistung hin. Ein gutes Modell besitzt eine Restdatenverteilung, die ihren Höhepunkt bei Null hat (mit wenigen Restdaten bei den Extremen). Ein weniger gutes Modell besitzt eine weit auseinander liegende Restdatenverteilung mit weniger Stichproben um Null herum.
Restdatendiagramm für ein gutes Modell
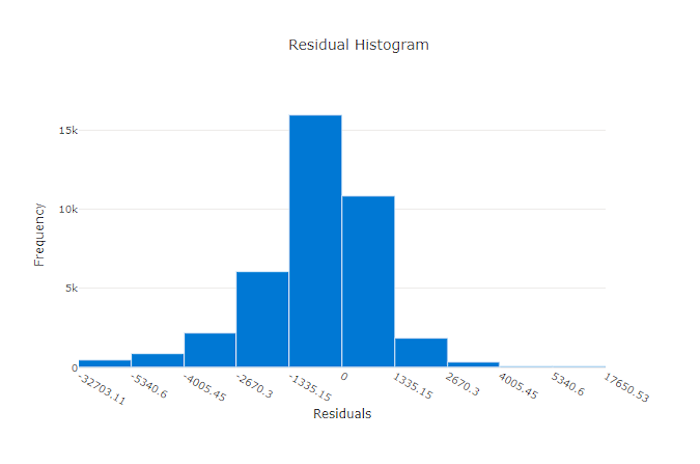
Restdatendiagramm für ein ungültiges Modell

Vorhergesagt im Vergleich zu den wahren Werten
Bei Regressions- und Vorhersageexperimenten stellt das Diagramm „Vorhergesagt im Vergleich zu den wahren Werten“ die Beziehung zwischen der Zielfunktion (wahre/tatsächliche Werte) und den Vorhersagen des Modells dar. Die wahren Werte werden entlang der X-Achse klassifiziert und für jede Klassifizierung wird der mittlere vorhergesagte Wert mit Fehlerindikatoren dargestellt. So können Sie erkennen, ob ein Modell bei der Vorhersage bestimmter Werte verzerrt ist. Die Linie zeigt die durchschnittliche Vorhersage und der schattierte Bereich zeigt die Varianz der Vorhersagen um diesen Mittelwert an.
Oft weist der häufigste wahre Wert die genauesten Vorhersagen mit der geringsten Varianz auf. Der Abstand der Trendlinie von der Ideallinie y = x, bei der es nur wenige wahre Werte gibt, ist ein gutes Maß für die Modellleistung bei Ausreißern. Sie können das Histogramm am unteren Rand des Diagramms verwenden, um Rückschlüsse auf die tatsächliche Datenverteilung zu ziehen. Das Einbeziehen von weiteren Datenstichproben, bei denen die Verteilung gering ist, kann die Leistung des Modells bei unbekannten Daten verbessern.
In diesem Beispiel ist zu beachten, dass das bessere Modell eine Linie für „Vorhergesagt im Vergleich zu den wahren Werten“ aufweist, die näher an der idealen y = x-Linie liegt.
Diagramm zu „Vorhergesagt im Vergleich zu den wahren Werten“ für ein gutes Modell
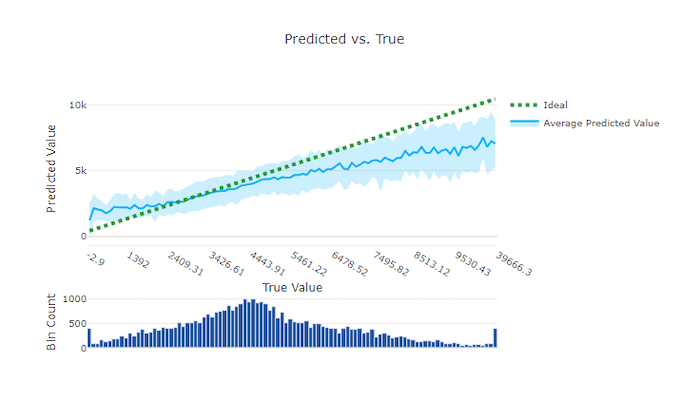
Diagramm zu „Vorhergesagt im Vergleich zu den wahren Werten“ für ein ungültiges Modell

Vorhersagehorizont
Bei Vorhersageexperimenten zeigt das Diagramm für den Vorhersagehorizont das Verhältnis zwischen dem vom Modell vorhergesagten Wert und den tatsächlichen Werten, die im Laufe der Zeit pro Kreuzvalidierungsfaltung bzw. Cross Validation Fold (bis zu fünf Faltungen) abgebildet werden. Die X-Achse bildet die Zeit auf der Grundlage der Frequenz ab, die Sie bei der Einrichtung des Trainings angegeben haben. Die vertikale Linie im Diagramm markiert den Vorhersagehorizont, der auch als Horizontlinie bezeichnet wird, d. h. den Zeitraum, in dem Sie mit der Erstellung von Vorhersagen beginnen möchten. Links von der Vorhersagehorizontlinie können Sie historische Trainingsdaten anzeigen, um vergangene Trends besser zu visualisieren. Rechts vom Vorhersagehorizont können Sie die Vorhersagen (violette Linie) im Vergleich zu den tatsächlichen Werten (blaue Linie) für die verschiedenen Kreuzvalidierungsfaltungen und Zeitreihenbezeichner sehen. Der schattierte violette Bereich zeigt die Konfidenzintervalle oder die Varianz der Vorhersagen um diesen Mittelwert an.
Sie können auswählen, welche Kombinationen von Kreuzvalidierungsfaltungen und Zeitreihenbezeichnern angezeigt werden sollen, indem Sie auf das Stiftsymbol in der oberen rechten Ecke des Diagramms klicken. Wählen Sie aus den ersten fünf Kreuzvalidierungsfaltungen und bis zu 20 verschiedenen Zeitreihenbezeichnern aus, um das Diagramm für Ihre verschiedenen Zeitreihen zu visualisieren.
Wichtig
Dieses Diagramm steht sowohl bei der Trainingsausführung für Modelle zur Verfügung, die aus Trainings- und Validierungsdaten generiert wurden, als auch bei der Testausführung, die auf Trainings- und Testdaten basiert. Wir lassen bis zu 20 Datenpunkte vor und bis zu 80 Datenpunkte nach dem Vorhersageursprung zu. Bei DNN-Modellen zeigt dieses Diagramm bei der Trainingsausführung die Daten der letzten Epoche an, d. h. nachdem das Modell vollständig trainiert worden ist. Dieses Diagramm kann bei der Testausführung eine Lücke vor der Horizontlinie aufweisen, wenn bei der Trainingsausführung explizit Validierungsdaten bereitgestellt wurden. Dies liegt daran, dass Trainingsdaten und Testdaten bei der Testausführung verwendet werden, wobei die Validierungsdaten weggelassen werden, wodurch eine Lücke entsteht.
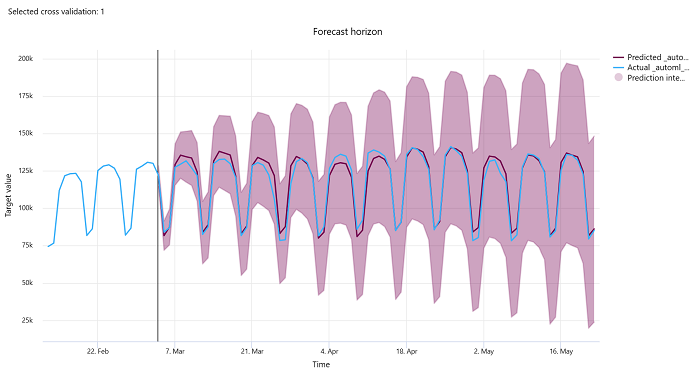
Metriken für Bildmodelle (Vorschau)
Automatisiertes ML verwendet die Bilder aus dem Validierungsdataset, um die Leistung des Modells auszuwerten. Die Leistung des Modells wird auf Epochenebene gemessen, um zu verstehen, wie das Training verläuft. Eine Epoche vergeht, wenn ein gesamtes Dataset das neuronale Netz genau einmal vorwärts und rückwärts durchlaufen hat.
Bildklassifizierungsmetriken
Die primäre Metrik zur Auswertung ist Genauigkeit für binäre und mehrklassige Klassifizierungsmodelle und IoU (Intersection over Union) für Multitagklassifizierungsmodelle. Die Klassifizierungsmetriken für Bildklassifizierungmodelle sind mit denen identisch, die im Abschnitt Klassifizierungsmetriken definiert sind. Die einer Epoche zugeordneten Verlustwerte werden ebenfalls protokolliert, was dabei helfen kann, den Trainingsfortschritt zu überwachen und zu ermitteln, ob das Modell über- oder unterangepasst ist.
Jede Vorhersage eines Klassifizierungsmodells wird einer Zuverlässigkeitsbewertung zugeordnet, welche den Grad der Zuverlässigkeit angibt, mit der die Vorhersage getroffen wurde. Multitag-Bildklassifizierungsmodelle werden standardmäßig mit einem Score-Schwellenwert von 0,5 ausgewertet. Dies bedeutet, dass nur Vorhersagen mit mindestens diesem Grad an Konfidenz als eine für die zugeordnete Klasse positive Vorhersage betrachtet wird. Die Multiklassen-Klassifizierung verwendet keinen Score-Schwellenwert. Stattdessen wird die Klasse mit der maximalen Konfidenzbewertung als Vorhersage betrachtet.
Metriken auf Epochenebene für die Bildklassifizierung
Anders als die Klassifizierungsmetriken für tabellarische Datasets protokollieren Bildungklassifizierungsmodelle alle Klassifizierungsmetriken wie unten dargestellt auf Epochenebene.

Zusammenfassungsmetriken für die Bildklassifizierung
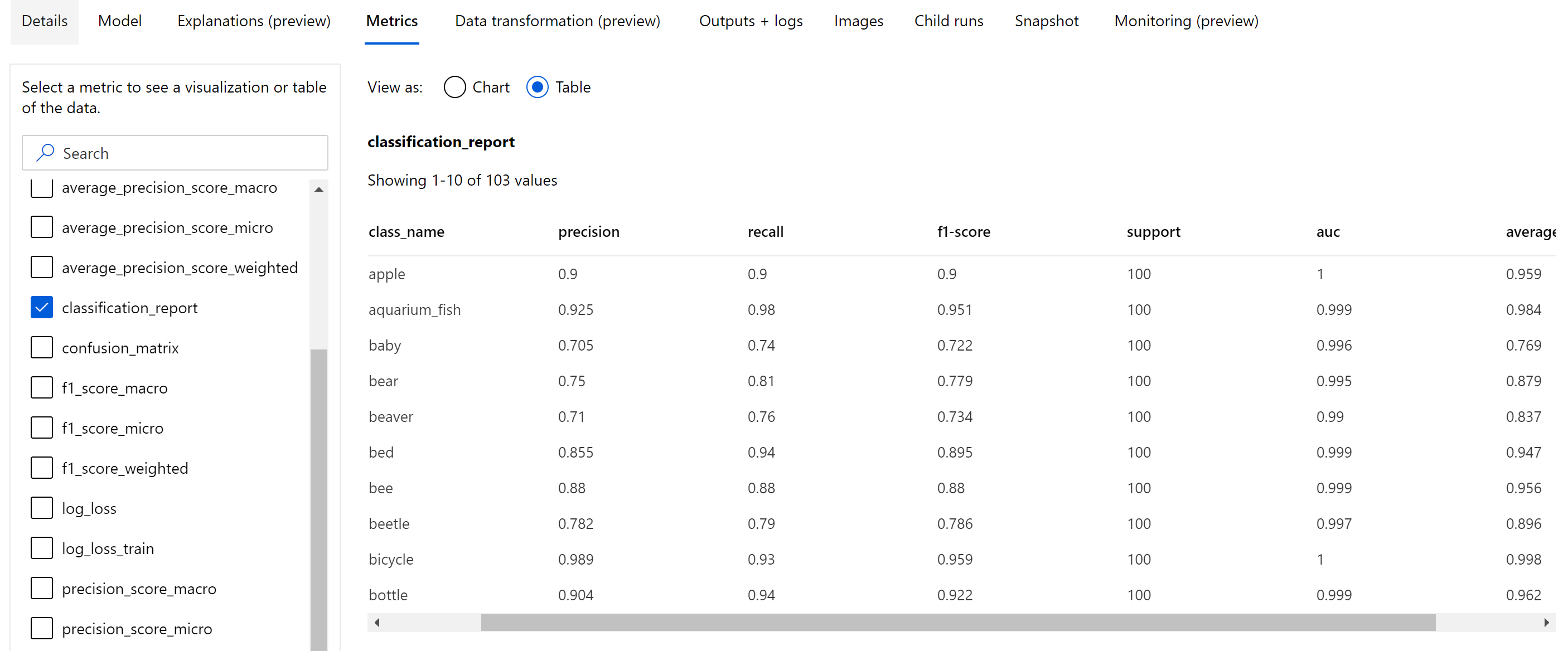
Abgesehen von den skalaren Metriken, die auf Epochenebene protokolliert werden, protokollieren Bildklassifizierungsmodelle auch Zusammenfassungsmetriken wie die Konfusionsmatrix und Klassifizierungsdiagramme wie ROC-Kurven, Kurven zu Genauigkeit und Abruf sowie Klassifizierungsberichte für das Modell aus der besten Epoche, in der die höchste Bewertung der primären Metrik (Genauigkeit) erhalten wird.
Wie im Folgenden dargestellt bietet der Klassifizierungsbericht Werte auf Klassenebene für Metriken wie „precision“, „recall“, „f1-score“, „support“, „auc“ und „average_precision“ mit verschiedenen Methoden zur Mittelwerterstellung: „macro“, „micro“ und „weighted“. Weitere Informationen finden Sie in den Metrikdefinitionen im Abschnitt Klassifizierungsmetriken.
Metriken zur Objekterkennung und Instanzsegmentierung
Zu jeder Vorhersage aus einem Bildobjekterkennungs- oder Instanzsegmentierungsmodell gibt es eine Zuverlässigkeitsbewertung.
Die Vorhersagen mit einer Zuverlässigkeitsbewertung, die höher ist als der Bewertungsschwellenwert, werden als Vorhersagen ausgegeben und in der Metrikberechnung verwendet, deren Standardwert modellspezifisch ist und auf die über die Seite zur Hyperparameteroptimierung (Hyperparameter box_score_threshold) verwiesen werden kann.
Die Metrikberechnung einer Bildobjekterkennung und eines Instanzsegmentierungsmodells basiert auf einer Überlappungsmessung, die von der Metrik IoU (Intersection over Union) definiert wird. Diese wird berechnet, indem der Bereich der Überlappung zwischen den Lerndaten und den Vorhersagen durch die Vereinigungsmenge der Lerndaten und den Vorhersagen geteilt wird. Die aus jeder Vorhersage berechnete IoU wird mit einem Überlappungsschwellenwert verglichen, der als IoU-Schwellenwert bezeichnet wird und bestimmt, in welchem Ausmaß eine Vorhersage mit benutzerannotierten Lerndaten überschneiden soll, um als positive Vorhersage betrachtet zu werden. Wenn der aus der Vorhersage berechnete IoU-Wert kleiner als der Überlappungsschwellenwert ist, wird die Vorhersage für die zugeordnete Klasse nicht als positiv betrachtet.
Die primäre Metrik zum Auswerten von Bildobjekterkennungs- und Instanzsegmentierungsmodellen ist die Mean Average Precision (mAP) . Die mAP ist der durchschnittliche Wert der durchschnittlichen Genauigkeit (Average Precision, AP) für alle Klassen. Objekterkennungsmodelle für automatisiertes ML unterstützen die Berechnung von mAP mithilfe der folgenden gängigen Methoden.
Pascal VOC-Metriken:
Pascal VOC-mAP ist die standardmäßige Art der mAP-Berechnung für Objekterkennungs- / Instanzsegmentierungsmodelle. Die mAP-Methode im Pascal-VOC-Stil berechnet den Bereich unter einer Version der Genauigkeits-Abruf-Kurve. Als erstes wird p(rᵢ), bei dem es sich um die Genauigkeit beim Abruf (i) handelt, für alle eindeutigen Abrufwerte berechnet. p(rᵢ) wird dann durch die maximale Genauigkeit ersetzt, die für jeden Abruf r' >= rᵢ abgerufen wird. Der Genauigkeitswert nimmt in dieser Version der Kurve monoton ab. Die Metrik Pascal VOC-maP wird standardmäßig mit einem IoU-Schwellenwert von 0,5 ausgewertet. Eine ausführliche Erläuterung dieses Konzepts finden Sie in diesem Blog.
COCO-Metriken:
COCO-Auswertungsmethoden verwenden eine interpolierte 101-Punkt-Methode für die Berechnung der durchschnittlichen Genauigkeit zusammen mit einer Mittelwerterstellung von mehr als zehn IoU-Schwellenwerten. AP@[.5:.95] entspricht der durchschnittlichen Genauigkeit für IoU von 0,5 bis 0,95 mit einer Schrittgröße von 0,05. Das automatisierte maschinelle Lernen protokolliert alle zwölf Metriken, die von der COCO-Methode definiert werden (einschließlich AP und AR in verschiedenen Skalierungen in den Anwendungsprotokollen), während auf der Benutzeroberfläche für Metriken nur die mAP mit einem IoU-Schwellenwert von 0,5 angezeigt wird.
Tipp
Die Auswertung des Bildobjekterkennungsmodells kann COCO-Metriken verwenden, wenn der Hyperparameter validation_metric_type wie im Abschnitt zur Hyperparameteroptimierung erläutert auf „COCO“ festgelegt ist.
Metriken auf Epochenebene für Objekterkennung und Instanzsegmentierung
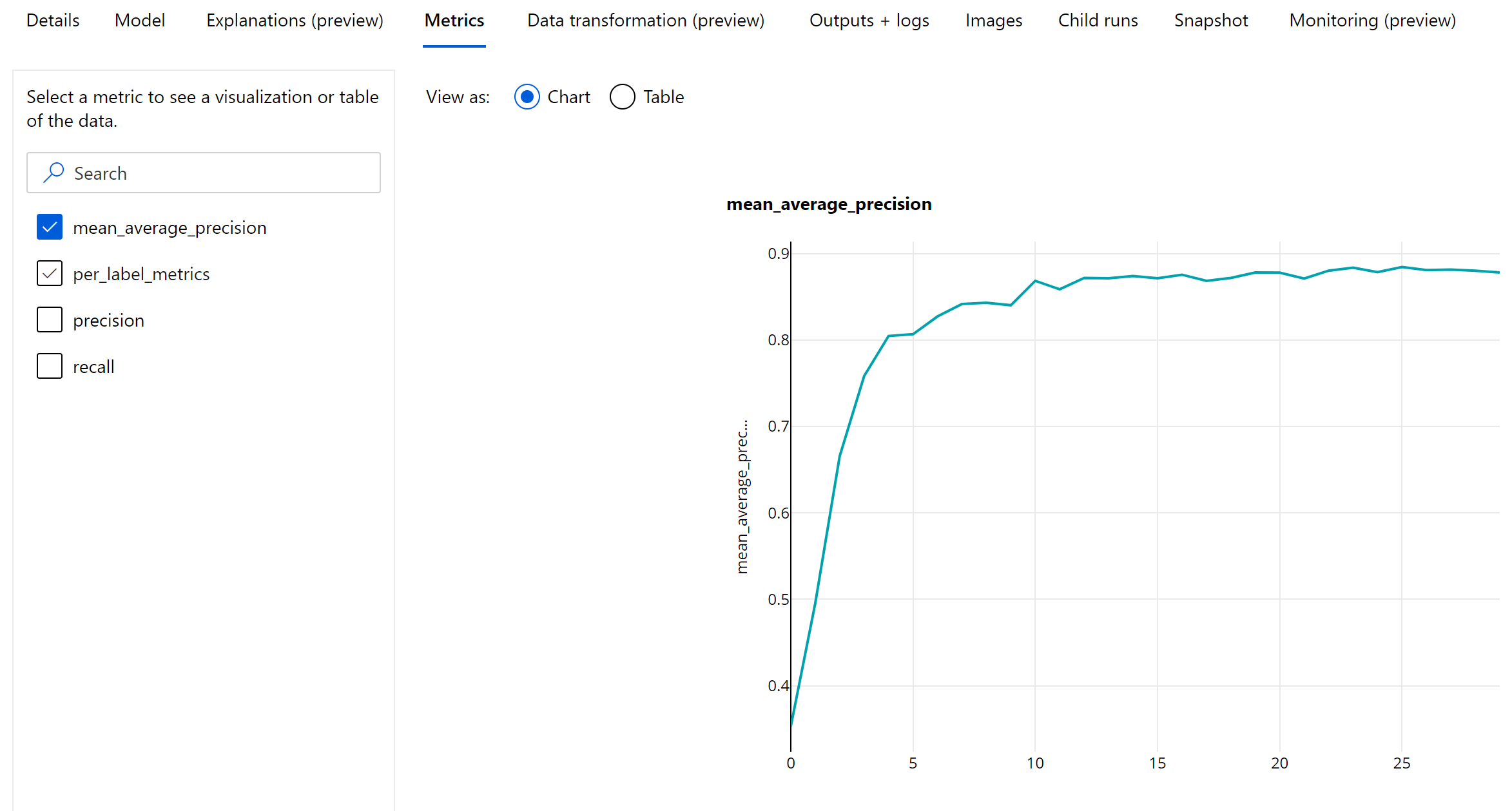
Die mAP-, Genauigkeits- und Abrufwerte werden auf Epochenebene für Bildobjekterkennungsmodelle bzw. Instanzsegmentierungsmodelle protokolliert. Die mAP-, Genauigkeits- und Abrufmetriken werden auch auf Klassenebene mit dem Namen „per_label_metrics“ protokolliert. Die „per_label_metrics“ sollten als Tabelle angezeigt werden.
Hinweis
Metriken auf Epochenebene für Genauigkeit, Abruf und „per_label_metrics“ sind bei der Verwendung der „COCO“-Methode nicht verfügbar.
Verantwortungsvolle KI-Dashboard für das am meisten empfohlene AutoML-Modell (Vorschau)
Das Dashboard „Verantwortungsvolle KI“ bietet eine einzige Benutzeroberfläche, die Ihnen dabei hilft, verantwortungsvolle KI in der Praxis effektiv und effizient zu implementieren. Verantwortungsvolle KI-Dashboard wird nur mithilfe tabellarischer Daten und nur für Klassifizierungs- und Regressionsmodelle unterstützt. Es vereint mehrere ausgereifte Tools für verantwortungsvolle KI in den folgenden Bereichen:
- Bewertung der Modellleistung und Fairness
- Durchsuchen von Daten
- Interpretierbarkeit beim maschinellen Lernen
- Fehleranalyse
Während Modellauswertungsmetriken und Diagramme gut zum Messen der allgemeinen Qualität eines Modells geeignet sind, sind Vorgänge wie die Überprüfung der Fairness des Modells, das Anzeigen seiner Erklärungen (auch bekannt als: welches Dataset enthält ein Modell, das zum Treffen seiner Vorhersagen verwendet wird) und das Überprüfen seiner Fehler und potenziellen Schwachpunkte beim Einsatz verantwortungsvoller KI von entscheidender Bedeutung. Aus diesem Grund bietet das automatisierte maschinelle Lernen ein verantwortungsvolles KI-Dashboard, mit dem Sie eine Vielzahl von Erkenntnissen für Ihr Modell beobachten können. Informationen zum Anzeigen des KI-Dashboards in Azure Machine Learning Studio.
Erfahren Sie, wie Sie diese Dashboard über die Benutzeroberfläche oder das SDK generieren können.
Modellerläuterung und Featurerelevanz
Während Metriken und Diagramme zur Modellauswertung gut geeignet sind, um die allgemeine Qualität eines Modells zu messen, ist die Überprüfung, welche Datasetfunktionen ein Modell für Vorhersagen verwendet hat, beim Einsatz verantwortungsvoller KI unerlässlich. Deshalb bietet das automatisierte maschinelle Lernen ein Modellerklärungsdashboard zum Messen und Melden der relativen Beiträge von Datasetfeatures. Informationen zum Anzeigen des Erklärungsdashboards in Azure Machine Learning Studio finden Sie hier.
Hinweis
Interpretierbarkeit, die Erklärung des besten Modells, ist nicht für Vorhersageexperimente mit automatisiertem maschinellem Lernen verfügbar, die die folgenden Algorithmen als bestes Modell oder Ensemble empfehlen:
- TCNForecaster
- AutoArima
- ExponentialSmoothing
- Prophet
- Durchschnitt
- Naiv
- Saisonaler Durchschnitt
- Saisonal naiv
Nächste Schritte
- Probieren Sie die Beispielnotebooks für die Modellerklärung zum automatisierten Machine Learning aus.
- Bei Fragen zum automatisierten maschinellen Lernen wenden Sie sich an askautomatedml@microsoft.com.