Transformationen (Direct3D 9)
Der Teil von Direct3D, der die Geometrie durch die Pipeline für die Geometrie fester Funktionen pusht, ist die Transformations-Engine. Es sucht das Modell und den Viewer in der Welt, projiziert Scheitelpunkte für die Anzeige auf dem Bildschirm und clipst Scheitelpunkte für den Viewport. Die Transformations-Engine führt auch Beleuchtungsberechnungen durch, um diffuse und spekuläre Komponenten an jedem Scheitelpunkt zu bestimmen.
Die Geometriepipeline akzeptiert Scheitelpunkte als Eingabe. Die Transformations-Engine wendet die Welt-, Ansichts- und Projektionstransformationen auf die Scheitelpunkte an, schneidet das Ergebnis ab und übergibt alles an den Rasterisierer.
Am Kopf der Pipeline werden die Scheitelpunkte eines Modells relativ zu einem lokalen Koordinatensystem deklariert. Dies ist ein lokaler Ursprung und eine Ausrichtung. Diese Ausrichtung von Koordinaten wird häufig als Modellraum bezeichnet, und einzelne Koordinaten werden als Modellkoordinaten bezeichnet.
Die erste Phase der Geometriepipeline transformiert die Scheitelpunkte eines Modells vom lokalen Koordinatensystem in ein Koordinatensystem, das von allen Objekten in einer Szene verwendet wird. Der Prozess der Neuausrichtung der Scheitelpunkte wird als Welttransformation bezeichnet. Diese neue Ausrichtung wird allgemein als Weltraum bezeichnet, und jeder Scheitelpunkt im Weltraum wird mithilfe von Weltkoordinaten deklariert.
In der nächsten Phase werden die Scheitelpunkte, die Ihre 3D-Welt beschreiben, in Bezug auf eine Kamera ausgerichtet. Das heißt, Ihre Anwendung wählt einen Standpunkt für die Szene aus, und die Koordinaten des Weltraums werden um die Kameraansicht verschoben und gedreht, sodass der Weltraum in Kameraraum umgewandelt wird. Dies ist die Ansichtstransformation.
Die nächste Phase ist die Projektionstransformation. In diesem Teil der Pipeline werden Objekte normalerweise in Bezug auf ihre Entfernung vom Betrachter skaliert, um einer Szene die Illusion der Tiefe zu verleihen; Close-Objekte werden so erstellt, dass sie größer erscheinen als entfernte Objekte usw. Der Einfachheit halber bezieht sich diese Dokumentation auf den Raum, in dem Scheitelpunkte nach der Projektionstransformation als Projektionsraum vorhanden sind. Einige Grafikbücher können den Projektionsraum als postperspektivenhohen Raum bezeichnen. Nicht alle Projektionstransformationen skalieren die Größe von Objekten in einer Szene. Eine solche Projektion wird manchmal als affine oder orthogonale Projektion bezeichnet.
Im letzten Teil der Pipeline werden alle Scheitelpunkte entfernt, die auf dem Bildschirm nicht sichtbar sind, sodass sich der Rasterisierer nicht die Zeit nimmt, die Farben und Schattierung für etwas zu berechnen, das nie angezeigt wird. Dieser Prozess wird als Clipping bezeichnet. Nach dem Clipping werden die verbleibenden Scheitelpunkte entsprechend den Viewportparametern skaliert und in Bildschirmkoordinaten konvertiert. Die resultierenden Scheitelpunkte, die auf dem Bildschirm zu sehen sind, wenn die Szene gerastert ist, sind im Bildschirmraum vorhanden.
Transformationen werden verwendet, um Objektgeometrie von einem Koordinatenraum in einen anderen zu konvertieren. Direct3D verwendet Matrizen, um 3D-Transformationen durchzuführen. In diesem Abschnitt wird erläutert, wie Matrizen 3D-Transformationen erstellen, einige häufige Verwendungen für Transformationen beschreibt und wie Sie Matrizen kombinieren können, um eine einzelne Matrix zu erzeugen, die mehrere Transformationen umfasst.
- World Transform (Direct3D 9): Konvertieren vom Modellraum in den Weltraum
- View Transform (Direct3D 9): Konvertieren von Weltraum in Sichtraum
- Projektionstransformation (Direct3D 9): Konvertieren vom Sichtraum in den Projektionsraum
Matrixtransformationen
In Anwendungen, die mit 3D-Grafiken arbeiten, können Sie geometrische Transformationen verwenden, um Folgendes auszuführen:
- Geben Sie die Position eines Objekts relativ zu einem anderen Objekt an.
- Drehen und Vergrößern von Objekten.
- Ändern Von Ansichtspositionen, Wegbeschreibungen und Perspektiven
Sie können jeden Punkt (x,y,z) in einen anderen Punkt (x', y', z') transformieren, indem Sie eine 4x4-Matrix verwenden, wie in der folgenden Gleichung gezeigt.
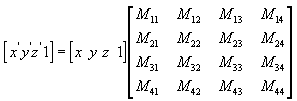
Führen Sie die folgenden Formeln für (x, y, z) und die Matrix aus, um den Punkt (x', y', z') zu erzeugen.
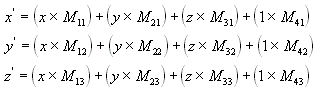
Die häufigsten Transformationen sind Übersetzung, Rotation und Skalierung. Sie können die Matrizen, die diese Effekte erzeugen, in einer einzigen Matrix kombinieren, um mehrere Transformationen gleichzeitig zu berechnen. Beispielsweise können Sie eine einzelne Matrix erstellen, um eine Reihe von Punkten zu übersetzen und zu rotieren.
Matrizen werden in Zeilen-Spaltenreihenfolge geschrieben. Eine Matrix, die Scheitelpunkte entlang jeder Achse gleichmäßig skaliert, die als einheitliche Skalierung bezeichnet wird, wird durch die folgende Matrix mit mathematischer Notation dargestellt.

In C++ deklariert Direct3D Matrizen unter Verwendung der D3DMATRIX-Struktur als zweidimensionales Array. Das folgende Beispiel zeigt, wie sie eine D3DMATRIX-Struktur initialisieren, um als einheitliche Skalierungsmatrix zu fungieren.
// In this example, s is a variable of type float.
D3DMATRIX scale = {
s, 0.0f, 0.0f, 0.0f,
0.0f, s, 0.0f, 0.0f,
0.0f, 0.0f, s, 0.0f,
0.0f, 0.0f, 0.0f, 1.0f
};
Übersetzung
Die folgende Gleichung übersetzt den Punkt (x, y, z) in einen neuen Punkt (x', y', z').
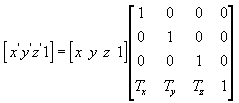
Sie können eine Übersetzungsmatrix in C++ manuell erstellen. Das folgende Beispiel zeigt den Quellcode für eine Funktion, die eine Matrix zum Übersetzen von Scheitelpunkten erstellt.
D3DXMATRIX Translate(const float dx, const float dy, const float dz) {
D3DXMATRIX ret;
D3DXMatrixIdentity(&ret);
ret(3, 0) = dx;
ret(3, 1) = dy;
ret(3, 2) = dz;
return ret;
} // End of Translate
Der Einfachheit halber stellt die D3DX-Hilfsprogrammbibliothek die D3DXMatrixTranslation-Funktion bereit .
Skalieren
Die folgende Formel skaliert den Punkt (x, y, z) um beliebige Werte in x-, y- und z-Richtung auf einen neuen Punkt (x', y', z').
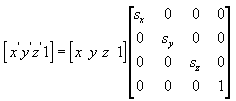
Rotate
Die hier beschriebenen Transformationen gelten für linkshändige Koordinatensysteme und unterscheiden sich daher möglicherweise von Transformationsmatrizen, die Sie an anderer Stelle gesehen haben.
Die folgende Formel rotiert den Punkt (x, y, z) um die x-Achse und erzeugt einen neuen Punkt (x', y', z').
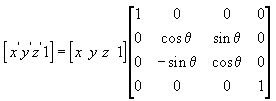
Mit der folgenden Gleichung wird der Punkt um die y-Achse gedreht.
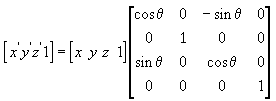
Mit der folgenden Formel wird der Punkt um die Z-Achse gedreht.
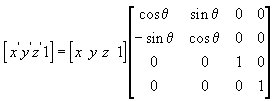
In diesen Beispielmatrizen steht der griechische Buchstabe theta für den Drehwinkel in Bogenmaß. Winkel werden im Uhrzeigersinn gemessen, wenn sie entlang der Drehachse zum Ursprung schauen.
Verwenden Sie in einer C++-Anwendung die Funktionen D3DXMatrixRotationX, D3DXMatrixRotationY und D3DXMatrixRotationZ , die von der D3DX-Hilfsprogrammbibliothek bereitgestellt werden, um Rotationsmatrizen zu erstellen. Im Folgenden ist der Code für die D3DXMatrixRotationX-Funktion aufgeführt.
D3DXMATRIX* WINAPI D3DXMatrixRotationX
( D3DXMATRIX *pOut, float angle )
{
#if DBG
if(!pOut)
return NULL;
#endif
float sin, cos;
sincosf(angle, &sin, &cos); // Determine sin and cos of angle
pOut->_11 = 1.0f; pOut->_12 = 0.0f; pOut->_13 = 0.0f; pOut->_14 = 0.0f;
pOut->_21 = 0.0f; pOut->_22 = cos; pOut->_23 = sin; pOut->_24 = 0.0f;
pOut->_31 = 0.0f; pOut->_32 = -sin; pOut->_33 = cos; pOut->_34 = 0.0f;
pOut->_41 = 0.0f; pOut->_42 = 0.0f; pOut->_43 = 0.0f; pOut->_44 = 1.0f;
return pOut;
}
Verkettung von Matrizen
Ein Vorteil der Verwendung von Matrizen ist, dass Sie die Effekte von zwei oder mehr Matrizen kombinieren können, indem Sie sie multiplizieren. Dies bedeutet, dass Sie nicht zwei Matrizen anwenden müssen, um ein Modell zu rotieren und es dann an einer bestimmten Stelle zu übersetzen. Stattdessen multiplizieren Sie die Rotations- und Übersetzungsmatrizen, um eine zusammengesetzte Matrix zu erzeugen, die alle ihre Effekte enthält. Dieser Prozess, der als Matrixverkettung bezeichnet wird, kann mit der folgenden Gleichung geschrieben werden.
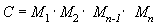
In dieser Gleichung ist C die zusammengesetzte Matrix, die erstellt wird, und M₁ bis Mn sind die einzelnen Matrizen. In den meisten Fällen werden nur zwei oder drei Matrizen verkettet, es gibt jedoch keine Begrenzung.
Verwenden Sie die D3DXMatrixMultiply-Funktion , um die Matrixmultiplikation durchzuführen.
Die Reihenfolge, in der die Matrixmultiplikation ausgeführt wird, ist von entscheidender Bedeutung. Die obige Formel spiegelt die Links-rechts-Regel der Matrixverkettung wider. Das heißt, die sichtbaren Auswirkungen der Matrizen, die Sie zum Erstellen einer zusammengesetzten Matrix verwenden, treten in der Reihenfolge von links nach rechts auf. Im folgenden Beispiel wird eine typische Weltmatrix gezeigt. Stellen Sie sich vor, Sie erstellen die Weltmatrix für eine stereotypische fliegende Untertasse. Wahrscheinlich möchten Sie die fliegende Untertasse um ihre Mitte drehen - die y-Achse des Modellraums - und sie an einen anderen Ort in Ihrer Szene übersetzen. Um diesen Effekt zu erzielen, erstellen Sie zuerst eine Rotationsmatrix und multiplizieren sie dann mit einer Übersetzungsmatrix, wie in der folgenden Gleichung gezeigt.
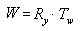
In dieser Formel ist Ry eine Matrix für die Drehung um die y-Achse, und Tw ist eine Übersetzung in eine Position in Weltkoordinaten.
Die Reihenfolge, in der Sie die Matrizen multiplizieren, ist wichtig, da die Matrixmultiplikation im Gegensatz zum Multiplizieren von zwei skalaren Werten nicht kommutativ ist. Das Multiplizieren der Matrizen in entgegengesetzter Reihenfolge hat den visuellen Effekt, die fliegende Untertasse in ihre Weltraumposition zu übersetzen und sie dann um den Weltursprung zu rotieren.
Unabhängig davon, welche Art von Matrix Sie erstellen, denken Sie an die Regel von links nach rechts, um sicherzustellen, dass Sie die erwarteten Effekte erzielen.
Zugehörige Themen