Rotaciones 3D en SkiaSharp
Use transformaciones no afines para girar objetos 2D en espacio 3D.
Una aplicación común de transformaciones no afines es simular la rotación de un objeto 2D en el espacio 3D:
Este trabajo implica trabajar con rotaciones tridimensionales y, a continuación, derivar una transformación no afín SKMatrix que realiza estas rotaciones 3D.
Es difícil desarrollar esta transformación SKMatrix trabajando únicamente dentro de dos dimensiones. El trabajo resulta mucho más fácil cuando esta matriz de 3 por 3 se deriva de una matriz de 4 por 4 utilizada en gráficos 3D. SkiaSharp incluye la clase SKMatrix44 para este propósito, pero son necesarios algunos conocimientos de gráficos 3D para entender las rotaciones 3D y la matriz de transformación de 4 por 4.
Un sistema de coordenadas tridimensional agrega un tercer eje denominado Z. Conceptualmente, el eje Z está en ángulos rectos a la pantalla. Los puntos de coordenadas en el espacio 3D se indican con tres números: (x, y, z). En el sistema de coordenadas 3D utilizado en este artículo, los valores crecientes de X van hacia la derecha y los valores crecientes de Y van hacia abajo, igual que en dos dimensiones. Los valores Z positivos crecientes salen de la pantalla. El origen es la esquina superior izquierda, al igual que en gráficos 2D. Puede considerar la pantalla como un plano XY con el eje Z en ángulos rectos a este plano.
Esto se denomina sistema de coordenadas izquierdas. Si apunta con el índice de la mano izquierda en la dirección de las coordenadas X positivas (hacia la derecha) y con el dedo corazón en la dirección de las coordenadas Y crecientes (hacia abajo), el pulgar apunta en la dirección de las coordenadas Z crecientes, extendiéndose hacia fuera de la pantalla.
En gráficos 3D, las transformaciones se basan en una matriz de 4 a 4. Esta es la matriz de identidades de 4 a 4:
| 1 0 0 0 | | 0 1 0 0 | | 0 0 1 0 | | 0 0 0 1 |
Al trabajar con una matriz de 4 a 4, es conveniente identificar las celdas con sus números de fila y columna:
| M11 M12 M13 M14 | | M21 M22 M23 M24 | | M31 M32 M33 M34 | | M41 M42 M43 M44 |
Sin embargo, la clase SkiaSharp Matrix44 es un poco diferente. La única manera de establecer u obtener valores de celda individuales en SKMatrix44 es mediante el indizador Item. Los índices de fila y columna se basan en cero en lugar de en uno, y las filas y columnas se intercambian. A la celda M14 del diagrama anterior se accede utilizando el indexador [3, 0] en un objeto SKMatrix44.
En un sistema gráfico 3D, un punto 3D (x, y, z) se convierte en una matriz de 1 a 4 para multiplicar por la matriz de transformación 4 a 4:
| M11 M12 M13 M14 |
| x y z 1 | × | M21 M22 M23 M24 | = | x' y' z' w' |
| M31 M32 M33 M34 |
| M41 M42 M43 M44 |
De forma análoga a las transformaciones 2D que tienen lugar en tres dimensiones, se supone que las transformaciones 3D tienen lugar en cuatro dimensiones. La cuarta dimensión se conoce como W y se supone que el espacio 3D existe dentro del espacio 4D donde las coordenadas W son iguales a 1. Las fórmulas de transformación son las siguientes:
x' = M11·x + M21·y + M31·z + M41
y' = M12·x + M22·y + M32·z + M42
z' = M13·x + M23·y + M33·z + M43
w' = M14·x + M24·y + M34·z + M44
Es obvio a partir de las fórmulas de transformación que las celdas M11, M22, M33 son factores de escala en las direcciones X, Y y Z, y M41, M42 y M43 son factores de traslación en las direcciones X, Y y Z.
Para volver a convertir estas coordenadas al espacio 3D en el que W es igual a 1, las coordenadas x', y' y z' se dividen por w':
x" = x' / w'
y" = y' / w'
z" = z' / w'
w" = w' / w' = 1
Esa división por w' proporciona perspectiva en el espacio 3D. Si w' es igual a 1, no se produce ninguna perspectiva.
Las rotaciones en el espacio 3D pueden ser bastante complejas, pero las rotaciones más sencillas son las que rodean los ejes X, Y y Z. Una rotación de ángulo α alrededor del eje X es esta matriz:
| 1 0 0 0 | | 0 cos(α) sin(α) 0 | | 0 –sin(α) cos(α) 0 | | 0 0 0 1 |
Los valores de X permanecen iguales cuando se someten a esta transformación. La rotación alrededor del eje Y deja los valores de Y sin cambios:
| cos(α) 0 –sin(α) 0 | | 0 1 0 0 | | sin(α) 0 cos(α) 0 | | 0 0 0 1 |
La rotación alrededor del eje Z es la misma que en los gráficos 2D:
| cos(α) sin(α) 0 0 | | –sin(α) cos(α) 0 0 | | 0 0 1 0 | | 0 0 0 1 |
El sentido de giro está implícito en la lateralidad del sistema de coordenadas. Se trata de un sistema para mano izquierda, por lo que si apunta con el pulgar de la mano izquierda hacia valores crecientes para un eje concreto —hacia la derecha para la rotación alrededor del eje X, hacia abajo para la rotación alrededor del eje Y y hacia usted para la rotación alrededor del eje Z—, la curva de los otros dedos indica la dirección de rotación para ángulos positivos.
SKMatrix44 tiene métodos estáticos generalizados CreateRotation y CreateRotationDegrees que permiten especificar el eje alrededor del cual se produce la rotación:
public static SKMatrix44 CreateRotationDegrees (Single x, Single y, Single z, Single degrees)
Para la rotación alrededor del eje X, establezca los tres primeros argumentos en 1, 0, 0. Para la rotación alrededor del eje Y, establézcalos en 0, 1, 0, y para la rotación alrededor del eje Z, establézcalos en 0, 0, 1.
La cuarta columna del 4 por 4 es para la perspectiva. SKMatrix44 no tiene métodos para crear transformaciones de perspectiva, pero puede crear una usted mismo mediante el código siguiente:
SKMatrix44 perspectiveMatrix = SKMatrix44.CreateIdentity();
perspectiveMatrix[3, 2] = -1 / depth;
La razón del nombre del argumento depth será evidente en breve. Ese código crea la matriz:
| 1 0 0 0 | | 0 1 0 0 | | 0 0 1 -1/depth | | 0 0 0 1 |
Las fórmulas de transformación dan como resultado el siguiente cálculo de w':
w' = –z / depth + 1
Esto sirve para reducir las coordenadas X e Y cuando los valores de Z son menores que cero (conceptualmente detrás del plano XY) y para aumentar las coordenadas X e Y para los valores positivos de Z. Cuando la coordenada Z es igual a depth, entonces w' es cero y las coordenadas se convierten en infinitas. Los sistemas gráficos tridimensionales se construyen alrededor de una metáfora de cámara, y el valor depth representa aquí la distancia de la cámara desde el origen del sistema de coordenadas. Si un objeto gráfico tiene una coordenada Z que está a depth unidades del origen, conceptualmente está tocando la lente de la cámara y se vuelve infinitamente grande.
Tenga en cuenta que probablemente usará este valor perspectiveMatrix en combinación con matrices de rotación. Si un objeto gráfico que se está rotando tiene coordenadas X o Y mayores que depth, es probable que la rotación de este objeto en el espacio 3D implique coordenadas Z mayores que depth. ¡Esto debe evitarse! Al crear perspectiveMatrix, desea establecer depth en un valor suficientemente grande para todas las coordenadas del objeto gráfico, independientemente de cómo se rote. Esto garantiza que nunca haya ninguna división por cero.
La combinación de rotaciones 3D y perspectiva requiere multiplicar matrices de 4 a 4. Para ello, SKMatrix44 define métodos de concatenación. Si A y B son objetos SKMatrix44, el siguiente código establece A igual a A × B:
A.PostConcat(B);
Cuando se usa una matriz de transformación de 4 por 4 en un sistema gráfico 2D, se aplica a objetos 2D. Estos objetos son planos y se supone que tienen coordenadas Z de cero. La multiplicación de transformación es un poco más sencilla que la transformación mostrada anteriormente:
| M11 M12 M13 M14 |
| x y 0 1 | × | M21 M22 M23 M24 | = | x' y' z' w' |
| M31 M32 M33 M34 |
| M41 M42 M43 M44 |
Ese valor 0 para z da lugar a fórmulas de transformación que no implican ninguna celda de la tercera fila de la matriz:
x' = M11·x + M21·y + M41
y' = M12·x + M22·y + M42
z' = M13·x + M23·y + M43
w' = M14·x + M24·y + M44
Además, la coordenada z' también es irrelevante aquí. Cuando se muestra un objeto 3D en un sistema gráfico 2D, se contrae a un objeto bidimensional ignorando los valores de coordenada Z. Las fórmulas de transformación son realmente solo estas dos:
x" = x' / w'
y" = y' / w'
Esto significa que la tercera fila y tercera columna de la matriz de 4 por 4 se puede ignorar.
Pero si es así, ¿por qué es necesaria la matriz de 4 por 4?
Aunque la tercera fila y la tercera columna de 4 a 4 son irrelevantes para las transformaciones bidimensionales, la tercera fila y columna sí desempeñan un papel previo cuando se multiplican varios valores SKMatrix44. Por ejemplo, supongamos que se multiplica la rotación alrededor del eje Y con la transformación de perspectiva:
| cos(α) 0 –sin(α) 0 | | 1 0 0 0 | | cos(α) 0 –sin(α) sin(α)/depth | | 0 1 0 0 | × | 0 1 0 0 | = | 0 1 0 0 | | sin(α) 0 cos(α) 0 | | 0 0 1 -1/depth | | sin(α) 0 cos(α) -cos(α)/depth | | 0 0 0 1 | | 0 0 0 1 | | 0 0 0 1 |
En el producto, la celda M14 ahora contiene un valor de perspectiva. Si desea aplicar esa matriz a objetos 2D, se eliminan la tercera fila y columna para convertirlos en una matriz de 3 a 3:
| cos(α) 0 sin(α)/depth | | 0 1 0 | | 0 0 1 |
Ahora se puede usar para transformar un punto 2D:
| cos(α) 0 sin(α)/depth |
| x y 1 | × | 0 1 0 | = | x' y' z' |
| 0 0 1 |
Las fórmulas de transformación son:
x' = cos(α)·x
y' = y
z' = (sin(α)/depth)·x + 1
Ahora divida todo por z':
x" = cos(α)·x / ((sin(α)/depth)·x + 1)
y" = y / ((sin(α)/depth)·x + 1)
Cuando los objetos 2D se giran con un ángulo positivo alrededor del eje Y, los valores X positivos retroceden al fondo, mientras que los valores X negativos pasan al primer plano. Los valores X parecen acercarse al eje Y (que se rige por el valor de coseno) a medida que las coordenadas más alejadas del eje Y se vuelven más pequeñas o más grandes a medida que se alejan o se acercan al espectador.
Si utiliza SKMatrix44, realice todas las operaciones de rotación y perspectiva 3D multiplicando varios valores de SKMatrix44. Entonces se puede extraer una matriz bidimensional de 3 por 3 a partir de la matriz de 4 por 4 utilizando la propiedad Matrix de la clase SKMatrix44. Esta propiedad devuelve un valor conocido SKMatrix.
La página Rotación 3D le permite experimentar con la rotación 3D. El archivo Rotation3DPage.xaml crea una instancia de cuatro controles deslizantes para establecer la rotación alrededor de los ejes X, Y y Z, y para establecer un valor de profundidad:
<ContentPage xmlns="http://xamarin.com/schemas/2014/forms"
xmlns:x="http://schemas.microsoft.com/winfx/2009/xaml"
xmlns:skia="clr-namespace:SkiaSharp.Views.Forms;assembly=SkiaSharp.Views.Forms"
x:Class="SkiaSharpFormsDemos.Transforms.Rotation3DPage"
Title="Rotation 3D">
<Grid>
<Grid.RowDefinitions>
<RowDefinition Height="Auto" />
<RowDefinition Height="Auto" />
<RowDefinition Height="Auto" />
<RowDefinition Height="Auto" />
<RowDefinition Height="Auto" />
<RowDefinition Height="Auto" />
<RowDefinition Height="Auto" />
<RowDefinition Height="Auto" />
<RowDefinition Height="*" />
</Grid.RowDefinitions>
<Grid.Resources>
<ResourceDictionary>
<Style TargetType="Label">
<Setter Property="HorizontalTextAlignment" Value="Center" />
</Style>
<Style TargetType="Slider">
<Setter Property="Margin" Value="20, 0" />
<Setter Property="Maximum" Value="360" />
</Style>
</ResourceDictionary>
</Grid.Resources>
<Slider x:Name="xRotateSlider"
Grid.Row="0"
ValueChanged="OnSliderValueChanged" />
<Label Text="{Binding Source={x:Reference xRotateSlider},
Path=Value,
StringFormat='X-Axis Rotation = {0:F0}'}"
Grid.Row="1" />
<Slider x:Name="yRotateSlider"
Grid.Row="2"
ValueChanged="OnSliderValueChanged" />
<Label Text="{Binding Source={x:Reference yRotateSlider},
Path=Value,
StringFormat='Y-Axis Rotation = {0:F0}'}"
Grid.Row="3" />
<Slider x:Name="zRotateSlider"
Grid.Row="4"
ValueChanged="OnSliderValueChanged" />
<Label Text="{Binding Source={x:Reference zRotateSlider},
Path=Value,
StringFormat='Z-Axis Rotation = {0:F0}'}"
Grid.Row="5" />
<Slider x:Name="depthSlider"
Grid.Row="6"
Maximum="2500"
Minimum="250"
ValueChanged="OnSliderValueChanged" />
<Label Grid.Row="7"
Text="{Binding Source={x:Reference depthSlider},
Path=Value,
StringFormat='Depth = {0:F0}'}" />
<skia:SKCanvasView x:Name="canvasView"
Grid.Row="8"
PaintSurface="OnCanvasViewPaintSurface" />
</Grid>
</ContentPage>
Observe que depthSlider se inicializa con un valor Minimum de 250. Esto implica que el objeto 2D que se gira aquí tiene coordenadas X e Y restringidas a un círculo definido por un radio de 250 píxeles alrededor del origen. Cualquier rotación de este objeto en el espacio 3D siempre dará como resultado valores de coordenadas inferiores a 250.
El archivo de código subyacente Rotation3DPage.cs se carga en un mapa de bits de 300 píxeles cuadrados:
public partial class Rotation3DPage : ContentPage
{
SKBitmap bitmap;
public Rotation3DPage()
{
InitializeComponent();
string resourceID = "SkiaSharpFormsDemos.Media.SeatedMonkey.jpg";
Assembly assembly = GetType().GetTypeInfo().Assembly;
using (Stream stream = assembly.GetManifestResourceStream(resourceID))
{
bitmap = SKBitmap.Decode(stream);
}
}
void OnSliderValueChanged(object sender, ValueChangedEventArgs args)
{
if (canvasView != null)
{
canvasView.InvalidateSurface();
}
}
...
}
Si la transformación 3D se centra en este mapa de bits, las coordenadas X e Y oscilan entre –150 y 150, mientras que las esquinas están a 212 píxeles del centro, por lo que todo está dentro del radio de 250 píxeles.
El controlador PaintSurface crea objetos SKMatrix44 basados en los controles deslizantes y los multiplica conjuntamente mediante PostConcat. El valor SKMatrix extraído del objeto SKMatrix44 final se rodea de transformaciones de traslación para centrar la rotación en el centro de la pantalla:
public partial class Rotation3DPage : ContentPage
{
SKBitmap bitmap;
public Rotation3DPage()
{
InitializeComponent();
string resourceID = "SkiaSharpFormsDemos.Media.SeatedMonkey.jpg";
Assembly assembly = GetType().GetTypeInfo().Assembly;
using (Stream stream = assembly.GetManifestResourceStream(resourceID))
{
bitmap = SKBitmap.Decode(stream);
}
}
void OnSliderValueChanged(object sender, ValueChangedEventArgs args)
{
if (canvasView != null)
{
canvasView.InvalidateSurface();
}
}
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
// Find center of canvas
float xCenter = info.Width / 2;
float yCenter = info.Height / 2;
// Translate center to origin
SKMatrix matrix = SKMatrix.MakeTranslation(-xCenter, -yCenter);
// Use 3D matrix for 3D rotations and perspective
SKMatrix44 matrix44 = SKMatrix44.CreateIdentity();
matrix44.PostConcat(SKMatrix44.CreateRotationDegrees(1, 0, 0, (float)xRotateSlider.Value));
matrix44.PostConcat(SKMatrix44.CreateRotationDegrees(0, 1, 0, (float)yRotateSlider.Value));
matrix44.PostConcat(SKMatrix44.CreateRotationDegrees(0, 0, 1, (float)zRotateSlider.Value));
SKMatrix44 perspectiveMatrix = SKMatrix44.CreateIdentity();
perspectiveMatrix[3, 2] = -1 / (float)depthSlider.Value;
matrix44.PostConcat(perspectiveMatrix);
// Concatenate with 2D matrix
SKMatrix.PostConcat(ref matrix, matrix44.Matrix);
// Translate back to center
SKMatrix.PostConcat(ref matrix,
SKMatrix.MakeTranslation(xCenter, yCenter));
// Set the matrix and display the bitmap
canvas.SetMatrix(matrix);
float xBitmap = xCenter - bitmap.Width / 2;
float yBitmap = yCenter - bitmap.Height / 2;
canvas.DrawBitmap(bitmap, xBitmap, yBitmap);
}
}
Cuando experimente con el cuarto control deslizante, observará que los distintos ajustes de profundidad no alejan el objeto del espectador, sino que alteran el alcance del efecto de perspectiva:
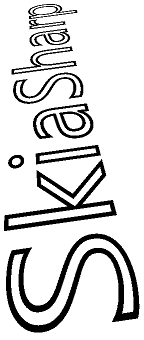
La rotación animada 3D también usa SKMatrix44 para animar una cadena de texto en el espacio 3D. El objeto textPaint establecido como campo se usa en el constructor para determinar los límites del texto:
public class AnimatedRotation3DPage : ContentPage
{
SKCanvasView canvasView;
float xRotationDegrees, yRotationDegrees, zRotationDegrees;
string text = "SkiaSharp";
SKPaint textPaint = new SKPaint
{
Style = SKPaintStyle.Stroke,
Color = SKColors.Black,
TextSize = 100,
StrokeWidth = 3,
};
SKRect textBounds;
public AnimatedRotation3DPage()
{
Title = "Animated Rotation 3D";
canvasView = new SKCanvasView();
canvasView.PaintSurface += OnCanvasViewPaintSurface;
Content = canvasView;
// Measure the text
textPaint.MeasureText(text, ref textBounds);
}
...
}
La invalidación OnAppearing define tres objetos Xamarin.FormsAnimation para animar los campos xRotationDegrees, yRotationDegrees y zRotationDegrees a diferentes velocidades. Observe que los períodos de estas animaciones se establecen en números primos (5 segundos, 7 segundos y 11 segundos), por lo que la combinación general solo se repite cada 385 segundos o más de 10 minutos:
public class AnimatedRotation3DPage : ContentPage
{
...
protected override void OnAppearing()
{
base.OnAppearing();
new Animation((value) => xRotationDegrees = 360 * (float)value).
Commit(this, "xRotationAnimation", length: 5000, repeat: () => true);
new Animation((value) => yRotationDegrees = 360 * (float)value).
Commit(this, "yRotationAnimation", length: 7000, repeat: () => true);
new Animation((value) =>
{
zRotationDegrees = 360 * (float)value;
canvasView.InvalidateSurface();
}).Commit(this, "zRotationAnimation", length: 11000, repeat: () => true);
}
protected override void OnDisappearing()
{
base.OnDisappearing();
this.AbortAnimation("xRotationAnimation");
this.AbortAnimation("yRotationAnimation");
this.AbortAnimation("zRotationAnimation");
}
...
}
Como en el programa anterior, el controlador PaintCanvas crea valores SKMatrix44 para la rotación y la perspectiva, y los multiplica conjuntamente:
public class AnimatedRotation3DPage : ContentPage
{
...
void OnCanvasViewPaintSurface(object sender, SKPaintSurfaceEventArgs args)
{
SKImageInfo info = args.Info;
SKSurface surface = args.Surface;
SKCanvas canvas = surface.Canvas;
canvas.Clear();
// Find center of canvas
float xCenter = info.Width / 2;
float yCenter = info.Height / 2;
// Translate center to origin
SKMatrix matrix = SKMatrix.MakeTranslation(-xCenter, -yCenter);
// Scale so text fits
float scale = Math.Min(info.Width / textBounds.Width,
info.Height / textBounds.Height);
SKMatrix.PostConcat(ref matrix, SKMatrix.MakeScale(scale, scale));
// Calculate composite 3D transforms
float depth = 0.75f * scale * textBounds.Width;
SKMatrix44 matrix44 = SKMatrix44.CreateIdentity();
matrix44.PostConcat(SKMatrix44.CreateRotationDegrees(1, 0, 0, xRotationDegrees));
matrix44.PostConcat(SKMatrix44.CreateRotationDegrees(0, 1, 0, yRotationDegrees));
matrix44.PostConcat(SKMatrix44.CreateRotationDegrees(0, 0, 1, zRotationDegrees));
SKMatrix44 perspectiveMatrix = SKMatrix44.CreateIdentity();
perspectiveMatrix[3, 2] = -1 / depth;
matrix44.PostConcat(perspectiveMatrix);
// Concatenate with 2D matrix
SKMatrix.PostConcat(ref matrix, matrix44.Matrix);
// Translate back to center
SKMatrix.PostConcat(ref matrix,
SKMatrix.MakeTranslation(xCenter, yCenter));
// Set the matrix and display the text
canvas.SetMatrix(matrix);
float xText = xCenter - textBounds.MidX;
float yText = yCenter - textBounds.MidY;
canvas.DrawText(text, xText, yText, textPaint);
}
}
Esta rotación 3D está rodeada de varias transformaciones 2D para mover el centro de rotación al centro de la pantalla y escalar el tamaño de la cadena de texto para que tenga la misma anchura que la pantalla:

