Courbes

Une courbe régulière est un ensemble de pixels mis en surbrillance sur un affichage raster (ou des points sur une page imprimée) qui définissent le périmètre (ou une partie du périmètre) d’une section conique. Une courbe irrégulière est un ensemble de pixels qui définissent une courbe qui ne correspond pas au périmètre d’une section conique. Le point de fin est exclu d’une courbe tout comme il est exclu d’une ligne.

Lorsqu’une application appelle l’une des fonctions de dessin de courbes, GDI décompose la courbe en un certain nombre de segments de traits discrets et extrêmement petits. Après avoir déterminé les points de terminaison (point de départ et point de fin) pour chacun de ces segments de ligne, GDI détermine quels pixels (ou points) définissent chaque ligne en appliquant son DDA.

Une application peut dessiner une ellipse ou une partie d’une ellipse en appelant la fonction Arc . Cette fonction dessine la courbe dans le périmètre d’un rectangle invisible appelé rectangle englobant. La taille de l’ellipse est spécifiée par deux radiales invisibles qui s’étendent du centre du rectangle aux côtés du rectangle. L’illustration suivante montre un arc (partie d’une ellipse) dessiné à l’aide de la fonction Arc .

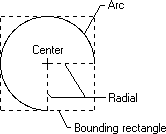
Lors de l’appel de la fonction Arc , une application spécifie les coordonnées du rectangle englobant et des radials. L’illustration précédente montre le rectangle et les radials avec des traits en pointillés tandis que l’arc réel a été dessiné à l’aide d’une ligne pleine.

Lors du dessin de l’arc d’un autre objet, l’application peut appeler les fonctions SetArcDirection et GetArcDirection pour contrôler la direction (dans le sens des aiguilles d’une montre ou dans le sens inverse des aiguilles d’une montre) dans laquelle l’objet est dessiné. La direction par défaut pour dessiner des arcs et d’autres objets est dans le sens inverse des aiguilles d’une montre.

En plus de dessiner des points de suspension ou des parties d’ellipses, les applications peuvent dessiner des courbes irrégulières appelées courbes de Bézier. Une courbe de Bézier est une courbe irrégulière dont la courbure est définie par quatre points de contrôle (p1, p2, p3 et p4). Les points de contrôle p1 et p4 définissent les points de début et de fin de la courbe, et les points de contrôle p2 et p3 définissent la forme de la courbe en marquant les points où la courbe inverse l’orientation, comme illustré dans le diagramme suivant.

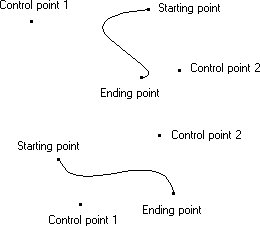
Une application peut dessiner des courbes irrégulières en appelant la fonction PolyBezier , en fournissant les points de contrôle appropriés.