Risultati dei modelli di Machine Learning
Questo articolo illustra le matrici di confusione, i problemi di classificazione e l'accuratezza nei modelli di apprendimento automatico. Lo scopo è migliorare la tua comprensione dell'accuratezza nei risultati della previsione ML. Il gruppo di destinatari di destinazione comprende tecnici, analisti e responsabili che desiderano sviluppare le proprie conoscenze e competenze nella data science.
Matrice di confusione
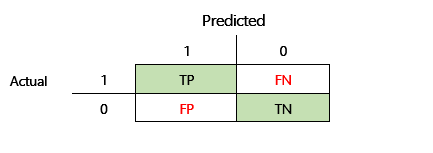
Dopo il training di un problema ML supervisionato su una serie di dati storici, viene testato utilizzando i dati che vengono conservati dal processo di training. In questo modo, puoi confrontare le previsioni del modello di training con i valori effettivi. La matrice di confusione fornisce un mezzo per valutare il successo di un problema di classificazione e dove vengono commessi errori (cioè, dove diventa "confuso").
Ad esempio, il tuo obiettivo è prevedere se un animale domestico è un cane o un gatto, in base ad alcuni attributi fisici e comportamentali. Se hai un set di dati di prova che contiene 30 cani e 20 gatti, la matrice di confusione potrebbe essere simile alla seguente illustrazione.

I numeri nelle celle verdi rappresentano le previsioni corrette. Come puoi vedere, il modello ha previsto correttamente una percentuale di gatti. La precisione complessiva del modello è facile da calcolare. In questo caso, è 42 ÷ 50 o 0,84.
Classificatori multi-classe in una matrice di confusione
La maggior parte delle discussioni sulla matrice di confusione si concentra sui classificatori binari, come nell'esempio precedente. Questo caso è un caso speciale in cui è possibile considerare altre metriche, come sensibilità e richiamo.
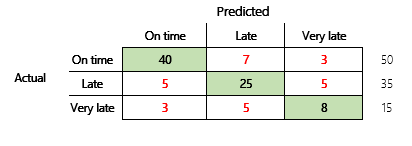
Successivamente, considereremo un problema di classificazione per uno scenario finanziario che ha tre stati. Il modello prevede se una fattura cliente verrà pagata in tempo, in ritardo o molto tardi. Ad esempio, su 100 fatture di prova, 50 vengono pagate in tempo, 35 vengono pagate in ritardo e 15 vengono pagate molto tardi. In questo caso, un modello potrebbe produrre una matrice di confusione simile alla seguente illustrazione.
 ]
]
Una matrice di confusione fornisce molte più informazioni rispetto a una semplice metrica di precisione. Tuttavia, è ancora relativamente facile da capire. Una matrice di confusione indica se disponi di un set di dati bilanciato in cui le classi di output hanno conteggi simili. Per lo scenario multi-classe, indica quanto potrebbe essere lontana una previsione quando le classi di output sono ordinali, come nell'esempio precedente sui pagamenti dei clienti.
Accuratezza del modello
Diverse metriche di accuratezza hanno il vantaggio di quantificare la qualità del modello.
Poiché l'accuratezza è una metrica facile da capire, è un buon punto di partenza per spiegare un modello ad altre persone, in particolare agli utenti del modello che non sono data scientist. Non è richiesta alcuna comprensione delle statistiche per comprendere l'accuratezza del modello. Quando è disponibile una matrice di confusione, fornisce ulteriori informazioni dettagliate sulle prestazioni del modello.
Tuttavia, per una comprensione più approfondita, è necessario notare diverse sfide associate alla precisione. L'utilità della metrica dipende dal contesto del problema. Una domanda che si pone spesso in relazione alle prestazioni del modello è: "Quanto è buono il modello?" Tuttavia, la risposta a questa domanda non è necessariamente semplice. Considera la seguente matrice di confusione (modello 2).
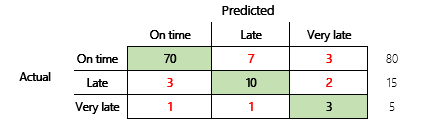
Un rapido calcolo mostra che l'accuratezza di questo modello è (70 + 10 + 3) ÷ 100 o 0,83. Ad un'occhiata superficiale, questo risultato sembra migliore del risultato per il precedente modello multi-classe (modello 1), che ha una precisione di 0,73. Ma è migliore?
Per iniziare ad affrontare questa domanda, considera l'accuratezza di un'ipotesi ingenua. Per un problema di classificazione, una semplice supposizione predice sempre la classe più comune. Per il modello 1, tale ipotesi sarà "puntuale" e produrrà una precisione di 0,50. Per il modello 2, tale ipotesi sarà "puntuale" e produrrà una precisione di 0,80. Poiché il modello 1 migliora l'ipotesi ingenua di 0,73 - 0,50 = 0,23, mentre il modello 2 migliora l'ipotesi ingenua di 0,83 - 0,80 = 0,03, il modello 1 è un modello migliore, anche se ha una precisione inferiore. Il calcolo rivela che una valutazione efficace della qualità di un modello richiede più contesto rispetto al valore di accuratezza.
Un altro aspetto è degno di nota. Considera uno scenario in cui viene utilizzato un test medico per individuare una malattia in un paziente. Questo problema è un problema di classificazione binaria in cui un risultato positivo indica che il paziente ha la malattia. In questo scenario, devi pensare all'impatto dei seguenti errori:
- Falsi positivi, dove il test dice che un paziente ha la malattia, ma in realtà non ce l'ha.
- Falsi negativi, dove il test dice che un paziente non ha la malattia, ma in realtà ce l'ha.
Ovviamente entrambi i tipi di errore non sono auspicabili, ma qual è il peggiore? Di nuovo, dipende. Nel caso di una malattia pericolosa per la vita che richiede un trattamento rapido, la riduzione al minimo dei falsi negativi (si spera seguita da test aggiuntivi) ha la priorità. In altre situazioni meno critiche, i creatori del modello potrebbero invece ridurre al minimo i falsi positivi. In ogni caso, una conclusione ragionevole è che per determinare in modo efficace la qualità di un modello, è necessario disporre di più informazioni di quelle fornite da una metrica di accuratezza.
Suggerimenti
La precisione è uno strumento importante per comunicare con esperti di dominio che non hanno familiarità con le statistiche. Tuttavia, per rendere utili le informazioni, è fondamentale fornire un contesto aggiuntivo insieme al valore di accuratezza.
Per lo scenario di previsione dei pagamenti, è possibile impostare un obiettivo per il modello ML che includa fattori in diversi comportamenti di pagamento. L'obiettivo è che il modello dovrebbe migliorare su un'ipotesi ingenua riducendo il numero di risposte errate di almeno il 50 percento. In altre parole, vuoi una precisione dell'obiettivo che divida la differenza tra l'accuratezza di un'ipotesi ingenua e il 100 percento.
La tabella seguente riassume questo principio per le matrici di confusione in questo articolo.
| Modello | Ipotesi ingenua | Destinazione | Accuratezza del modello | L'obiettivo è stato raggiunto? |
|---|---|---|---|---|
| Modello 1 | 0.50 | 0.75 | 0.73 | Quasi. Questo modello migliora notevolmente l'ipotesi. |
| Modello 2 | 0.80 | 0.90 | 0.83 | N. È necessario un miglioramento. |
Accuratezza F1 della classificazione
L'ultima considerazione in questo articolo è una misura più avanzata delle prestazioni di classificazione ML nota come precisione F1.
Prima di poter definire l'accuratezza F1, è necessario introdurre due metriche aggiuntive: precisione e richiamo. La precisione indica quante del numero totale di previsioni specificate come positive sono state assegnate correttamente. Questa metrica è nota anche come valore predittivo positivo. Il richiamo è il numero totale di casi positivi effettivi previsti correttamente. Questa metrica è nota anche come sensibilità.
Nella matrice di confusione nell'illustrazione precedente, queste metriche vengono calcolate nel modo seguente:
- Precisione = TP ÷ (TP + FP)
- Richiamo = TP ÷ (TP + FN)
La misura F1 combina precisione e richiamo. Il risultato è la media armonica dei due valori. Viene calcolato nel modo seguente:
- F1 = 2 × (Precisione × Richiamo) ÷ (Precisione + Richiamo)
Vediamo un esempio concreto. In precedenza in questo articolo, abbiamo utilizzato un esempio di un modello che prevedeva se un animale era un cane o un gatto. L'illustrazione è ripetuta qui.
Ecco i risultati se "Cane" viene utilizzato come risposta positiva.
- Precisione = 24 ÷ (24 + 2) = 0,9231
- Richiamo = 24 ÷ (24 + 6) = 0,8
- F1 = 2 × (0,9231 × 0,8) ÷ (0,9231 + 0,8) = 0,8572
Come puoi vedere, il valore F1 è compreso tra i valori di precisione e richiamo.
Sebbene l'accuratezza F1 non sia così facile da capire, aggiunge sfumature al numero di accuratezza di base. Può anche aiutare con set di dati non bilanciati, come mostrerà la discussione seguente.
La sezione Accuratezza del modello di questo articolo ha confrontato le seguenti due matrici di confusione. Anche se il primo modello aveva un'accuratezza inferiore, è stato ritenuto un modello più utile perché mostrava un miglioramento maggiore rispetto all'ipotesi predefinita di un pagamento puntuale.


Vediamo come si confrontano questi due modelli quando viene utilizzato il punteggio F1. Il punteggio F1 tiene conto della precisione e del richiamo per ogni stato, quindi il calcolo macro F1 calcola la media del punteggio F1 negli stati per determinare un punteggio F1 complessivo. Esistono altre varianti F1, ma è di maggior interesse considerare la versione macro, vista la stessa considerazione che viene data a tutti e tre gli stati.
Per semplificare i calcoli, sono stati creati array di esempio per abbinare i valori effettivi e previsti. Questi array hanno utilizzato la libreria di metriche di sklearn in Python per calcolare i valori. Questo è il risultato.
| Modello | Ipotesi ingenua | Precisione | Macro F1 |
|---|---|---|---|
| Modello 1 | 0.5 | 0.73 | 0.67 |
| Modello 2 | 0.80 | 0.83 | 0.66 |
Per maggiori dettagli su come funziona questo calcolo, ecco il report di classificazione sklearn.metrics per il modello 1. I tre stati, "Puntuale", "In ritardo" e "Molto tardi", sono rappresentati dalle righe contrassegnate rispettivamente con 1, 2 e 3. La media macro è solo la media della colonna "f1-score".
| precisione | richiamo | f1-score | |
|---|---|---|---|
| 1 | 0.83 | 0.80 | 0.82 |
| 2 | 0.68 | 0.71 | 0.69 |
| 3 | 0.50 | 0.50 | 0.50 |
Come mostrano questi risultati, i due modelli hanno punteggi di accuratezza macro F1 quasi identici. In questo e in molti altri casi, l'accuratezza F1 fornisce un migliore indicatore delle capacità di un modello. Per quanto riguarda l'accuratezza, l'interpretazione dei risultati richiede la comprensione di ciò che è più importante considerare nel modello.