Classificazione binaria
La classificazione, come la regressione, è una tecnica di Machine Learning supervisionata; pertanto, segue lo stesso processo iterativo di training, convalida e valutazione dei modelli. Anziché calcolare valori numerici come un modello di regressione, gli algoritmi usati per eseguire il training dei modelli di classificazione calcolano i valori di probabilità per l'assegnazione della classe e le metriche di valutazione usate per valutare le prestazioni del modello confrontano le classi stimate con le classi effettive.
Gli algoritmi di classificazione binaria vengono usati per eseguire il training di un modello che stima una delle due etichette possibili per una singola classe. Essenzialmente, la stima di vero o falso. Nella maggior parte degli scenari reali, le osservazioni dei dati usate per eseguire il training e la convalida del modello sono costituite da più valori di funzionalità (x) e da un valore ypari a 1 o 0.
Esempio: classificazione binaria
Per comprendere il funzionamento della classificazione binaria, si esamini un esempio semplificato che usa una singola funzionalità (x) per stimare se l'etichetta y è 1 o 0. In questo esempio si userà il livello di glucosio nel sangue per stimare se il paziente ha o meno il diabete. Ecco i dati con cui verrà eseguito il training del modello:
 |
 |
|---|---|
| Glucosio nel sangue (x) | Diabetico? (y) |
| 67 | 0 |
| 103 | 1 |
| 114 | 1 |
| 72 | 0 |
| 116 | 1 |
| 65 | 0 |
Valutazione di un modello di classificazione binaria
Per eseguire il training del modello, si userà un algoritmo per adattare i dati di training a una funzione che calcola la probabilità che l'etichetta di classe sia vera (in altre parole, che il paziente abbia il diabete). La probabilità viene misurata come valore compreso tra 0,0 e 1,0, in modo che la probabilità totale per tutte le classi possibili sia 1,0. Ad esempio, se la probabilità stimata che un paziente sia diabetico è 0,7, esiste una corrispondente probabilità dello 0,3 che il paziente non sia diabetico.
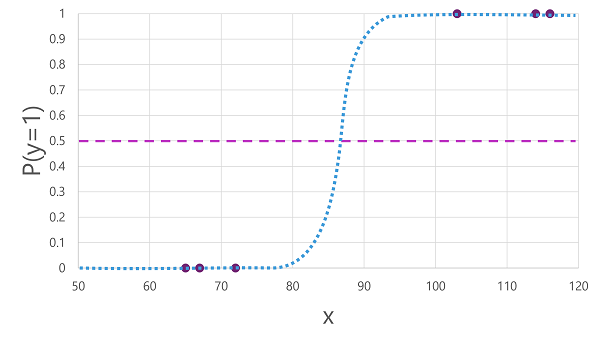
Esistono molti algoritmi che possono essere usati per la classificazione binaria, ad esempio la regressione logistica, da cui deriva una funzione sigmoide (a forma di S) con valori compresi tra 0,0 e 1,0, come illustrato di seguito:
Nota
Nonostante il nome, nel Machine Learning la regressione logistica viene usata per la classificazione, non per la regressione. L'aspetto importante è la natura logistica della funzione prodotta, che descrive una curva a forma di S tra un valore inferiore e uno superiore (0,0 e 1,0 quando si usa la classificazione binaria).
La funzione prodotta dall'algoritmo descrive la probabilità che y sia vera (y=1) per un determinato valore x. Matematicamente, è possibile esprimere la funzione come segue:
f(x) = P(y=1 | x)
Per tre delle sei osservazioni presenti nei dati di training, si sa che y è sicuramente vera, di conseguenza la probabilità per quelle osservazioni che y =1 è 1,0 e per le altre tre si sa che y è sicuramente falsa, di conseguenza la probabilità che y =1 è 0,0. La curva a forma di S descrive la distribuzione delle probabilità in modo che tracciando un valore di x sulla linea si identifica la probabilità corrispondente che y sia 1.
Il diagramma include anche una linea orizzontale per indicare la soglia in cui un modello basato su questa funzione stimerà vero (1) o falso (0). La soglia si trova nel punto medio per y (P(y) = 0,5). Per qualsiasi valore pari o superiore a questo punto, il modello stimerà vero (1); mentre per qualsiasi valore inferiore a questo punto stimerà falso (0). Ad esempio, per un paziente con un livello di glucosio nel sangue pari a 90, la funzione fornirà un valore di probabilità pari a 0,9. Dal momento che 0,9 è superiore alla soglia di 0,5, il modello stimerà vero (1); in altre parole, si prevede che il paziente abbia il diabete.
Valutazione di un modello di classificazione binaria
Come per la regressione, quando si esegue il training di un modello di classificazione binaria si trattiene un subset casuale di dati con cui convalidare il modello sottoposto a training. Si supponga di aver trattenuto i dati seguenti per convalidare il classificatore di diabete:
| Glucosio nel sangue (x) | Diabetico? (y) |
|---|---|
| 66 | 0 |
| 107 | 1 |
| 112 | 1 |
| 71 | 0 |
| 87 | 1 |
| 89 | 1 |
Applicando la funzione logistica derivata in precedenza ai valori x si ottiene il seguente grafico.
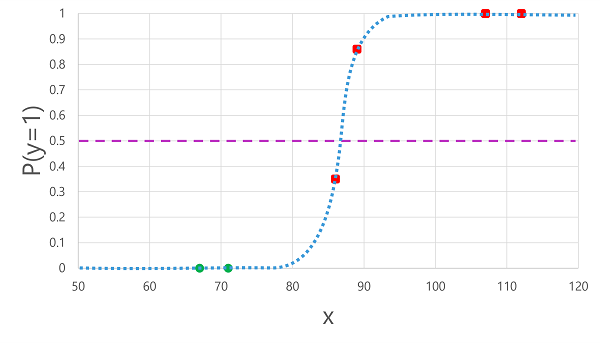
In base al fatto che la probabilità calcolata dalla funzione sia superiore o inferiore alla soglia, il modello genera un'etichetta stimata pari a 1 o 0 per ogni osservazione. È quindi possibile confrontare le etichette di classe stimate (ŷ) con le etichette di classe effettive (y), come illustrato di seguito:
| Glucosio nel sangue (x) | Diagnosi effettiva del diabete (y) | Diagnosi stimata del diabete (ŷ) |
|---|---|---|
| 66 | 0 | 0 |
| 107 | 1 | 1 |
| 112 | 1 | 1 |
| 71 | 0 | 0 |
| 87 | 1 | 0 |
| 89 | 1 | 1 |
Metriche di valutazione della classificazione binaria
Il primo passaggio per calcolare le metriche di valutazione di un modello di classificazione binaria consiste in genere nel creare una matrice del numero di stime corrette ed errate per ogni etichetta di classe possibile:
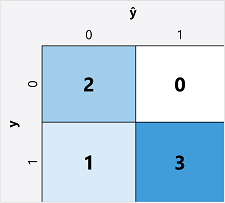
Questa visualizzazione è denominata matrice di confusione e mostra i totali della stima in cui:
- ŷ=0 e y=0: veri negativi (TN)
- ŷ=1 e y=0: Falsi positivi (FP)
- ŷ=0 e y=1: Falsi negativi (FN)
- ŷ=1 e y=1: veri positivi (TP)
La disposizione della matrice di confusione è tale che le previsioni corrette (vere) sono mostrate in una linea diagonale che va da in alto a sinistra fino a in basso a destra. L’intensità del colore spesso viene usata per indicare il numero di stime in ogni cella, in modo che un rapido sguardo a un modello in grado di formulare stime accurate riveli una tendenza diagonale fortemente ombreggiata.
Accuratezza
La metrica più semplice che è possibile calcolare tramite la matrice di confusione è l'accuratezza, ossia la percentuale di predizioni corrette da parte del modello. L'accuratezza viene calcolata come segue:
(TN+TP) ÷ (TN+FN+FP+TP)
Nel caso dell'esempio del diabete, il calcolo è il seguente:
(2+3) ÷ (2+1+0+3)
= 5 ÷ 6
= 0.83
Pertanto, per i dati di convalida, il modello di classificazione del diabete ha prodotto stime corrette nell’83% dei casi.
L'accuratezza potrebbe inizialmente sembrare una buona metrica per valutare un modello. Tuttavia, è necessario prendere in considerazione quanto segue. Si supponga che l’11% della popolazione sia affetta da diabete. È possibile creare un modello che stima sempre 0 e ottenere un'accuratezza dell'89%, sebbene non faccia alcun tentativo di differenziare i pazienti valutando le loro caratteristiche. Ciò di cui si ha realmente bisogno è una comprensione più approfondita del modo in cui il modello si comporta nel stimare 1 per i casi positivi e 0 per i casi negativi.
Richiamo
Il richiamo è una metrica che misura la percentuale di casi positivi identificati correttamente dal modello. In altre parole, rispetto al numero di pazienti affettida diabete, quanti ne ha stimati il modello?
La formula per il richiamo è:
TP ÷ (TP+FN)
Nel caso dell’esempio del diabete:
3 ÷ (3+1)
= 3 ÷ 4
= 0.75
Il modello quindi ha identificato correttamente il 75% dei pazienti affetti da diabete.
Precisione
La precisione è una metrica simile al richiamo, ma misura la percentuale di casi positivi stimati in cui l'etichetta vero è effettivamente positiva. In altre parole, quale percentuale dei pazienti stimati dal modello ha effettivamente il diabete?
La formula per la precisione è:
TP ÷ (TP+FP)
Nel caso dell’esempio del diabete:
3 ÷ (3+0)
= 3 ÷ 3
= 1.0
Quindi il 100% dei pazienti che il modello stima come affetti da diabete lo sono effettivamente.
Punteggio F1
Il punteggio F1 è una metrica complessiva che combina richiamo e precisione. La formula per il punteggio F1 è:
(2 x Precisione x Richiamo) ÷ (Precisione + Richiamo)
Nel caso dell’esempio del diabete:
(2 x 1.0 x 0.75) ÷ (1.0 + 0.75)
= 1.5 ÷ 1.75
= 0.86
Area sottesa alla curva (AUC)
Un altro nome per il richiamo è tasso di veri positivi (TPR), ed esiste una metrica equivalente chiamata tasso di falsi positivi (FPR) che si calcola con la formula FP÷(FP+TN). È già noto che il TPR per il modello quando si usa una soglia pari a 0,5 è 0,75 ed è possibile usare la formula per FPR per calcolare un valore pari a 0÷2 = 0.
Naturalmente, se si modificasse la soglia al di sopra della quale il modello stima vero (1), si influirebbe sul numero di stime positive e negative e quindi si modificherebbero le metriche TPR e FPR. Queste metriche vengono spesso usate per valutare un modello tracciando una curva delle caratteristiche dell'operatore ricevente (ROC) che mette a confronto il TPR e l'FPR per ogni possibile valore di soglia compreso tra 0,0 e 1,0:
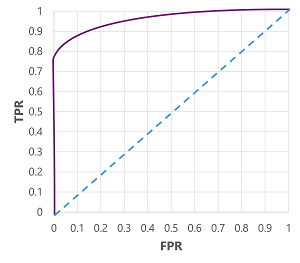
La curva ROC per un modello perfetto andrebbe dritta lungo l'asse TPR a sinistra e poi attraverso l'asse FPR in alto. Poiché l'area del tracciato per la curva misura 1x1, l'area sotto questa curva perfetta sarebbe 1,0 (il che significa che il modello è corretto il 100% delle volte). Al contrario, una linea diagonale che va dal basso a sinistra verso l'alto a destra rappresenta i risultati che si otterrebbero indovinando casualmente un'etichetta binaria, producendo un'area sotto la curva pari a 0,5. In altre parole, date due possibili etichette di classe, ci si può ragionevolmente aspettare di indovinare il 50% delle volte.
Nel caso del modello di diabete, viene prodotta la curva precedente e l'area sottesa alla curva (AUC) è 0,875. Poiché l'AUC è superiore a 0,5, è possibile concludere che il modello è più efficace nella stima della presenza o meno del diabete rispetto a un'ipotesi casuale.