Deep Learning

• 12 minuti

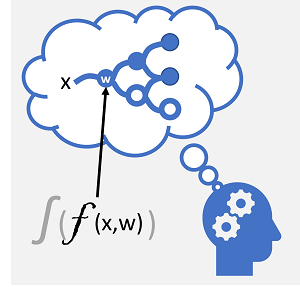
Il Deep Learning è una forma avanzata di Machine Learning che cerca di emulare il modo in cui il cervello umano apprende. La chiave per l'apprendimento avanzato è la creazione di una rete neurale artificiale che simula l'attività elettrochimica nei neuroni biologici usando funzioni matematiche, come illustrato di seguito.

Rete neurale biologica	Rete neurale artificiale
I neuroni si attivano in risposta agli stimoli elettrochimici. Quando viene attivato, il segnale viene passato ai neuroni connessi.	Ogni neurone è una funzione che opera su un valore di input (x) e un peso (w). La funzione viene sottoposta a wrapping in una funzione di attivazione che determina se trasmettere l'output.

Le reti neurali artificiali sono costituite da più strati di neuroni, che definiscono essenzialmente una funzione profondamente annidata. Questa architettura è il motivo per cui la tecnica viene denominata Deep Learning e i modelli da essa prodotti reti neurali profonde (DNN). È possibile usare reti neurali profonde per molti tipi di problemi di Machine Learning, tra cui regressione e classificazione, nonché modelli più specializzati per l'elaborazione del linguaggio naturale e la visione artificiale.

Analogamente ad altre tecniche di Machine Learning descritte in questo modulo, il Deep Learning prevede l'adattamento dei dati di training a una funzione in grado di stimare un'etichetta (y) in base al valore di una o più funzionalità (x). La funzione (f(x)) è lo strato esterno di una funzione annidata in cui ogni strato della rete neurale incapsula funzioni che operano su x e sui valori di peso (w) ad esse associati. L'algoritmo usato per eseguire il training del modello prevede di far passare in modo iterativo i valori delle funzionalità (x) nei dati di training attraverso gli strati per calcolare i valori di output per ŷ, di convalidare il modello per valutare quanto i valori di ŷ calcolati si discostino dai valori di y noti (il che quantifica il livello di errore, o perdita, nel modello) e quindi di modificare i pesi (w) per ridurre la perdita. Il modello sottoposto a training include i valori dei pesi finali che generano stime più accurate.

Esempio: uso di Deep Learning per la classificazione

Per comprendere meglio il funzionamento di un modello di rete neurale profonda, si esamini ora un esempio in cui una rete neurale viene usata per definire un modello di classificazione delle specie di pinguini.

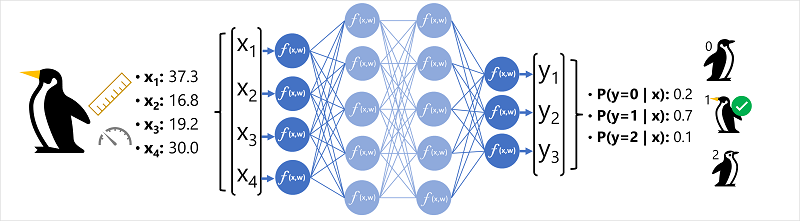
I dati relativi alle caratteristiche ( x) sono costituiti da alcune misurazioni eseguite su un pinguino. In particolare, le misure riguardano:

• Lunghezza del becco del pinguino.
• Profondità del becco del pinguino.
• Lunghezza della pinna del pinguino.
• Peso del pinguino.

In questo caso, x rappresenta un vettore di quattro valori, o matematicamente, x=[x1,x2,x3,x4].

Si supponga che l'etichetta che si sta tentando di stimare (y) sia la specie del pinguino e che le possibili specie siano tre:

• Adelia
• Gentoo
• Sottogola

Questo è un esempio di problema di classificazione, in cui il modello di Machine Learning deve stimare la classe più probabile a cui appartiene l'osservazione. Un modello di classificazione consente di ottenere questo risultato stimando un'etichetta costituita dalla probabilità per ogni classe. In altre parole, y è un vettore di tre valori di probabilità, una per ognuna delle possibili classi: [P(y=0|x), P(y=1|x), P(y=2|x)].

Il processo di inferenza di una classe di pinguini stimata usando questa rete è il seguente:

1. Il vettore di caratteristiche per l'osservazione di un pinguino viene immesso nello strato di input della rete neurale, che consiste in un neurone per ogni valore x. In questo esempio, il vettore x seguente viene usato come input: [37.3, 16.8, 19.2, 30.0]
2. Le funzioni per il primo strato di neuroni calcolano ciascuna una somma ponderata combinando il valore x e il peso w, e la passano a una funzione di attivazione che determina se soddisfa la soglia per passare allo strato successivo.
3. Ogni neurone di uno strato è connesso a tutti i neuroni dello strato successivo (un'architettura a volte definita rete completamente connessa), in modo che i risultati di ogni strato vengano inoltrati attraverso la rete fino a raggiungere lo strato di output.
4. Lo strato di output produce un vettore di valori; in questo caso, usa una funzione softmax o simile per calcolare la distribuzione di probabilità delle tre possibili classi di pinguini. In questo esempio, il vettore di output è: [0.2, 0.7, 0.1]
5. Gli elementi del vettore rappresentano le probabilità per le classi 0, 1 e 2. Il secondo valore è il più alto, quindi il modello stima che la specie del pinguino sia 1 (Gentoo).

In che modo viene appresa una rete neurale?

I pesi di una rete neurale sono fondamentali per calcolare i valori stimati per le etichette. Durante il processo di training, il modello apprende i pesi che determineranno le stime più accurate. Si esamini ora il processo di training in modo più dettagliato per comprendere come avviene questo apprendimento.

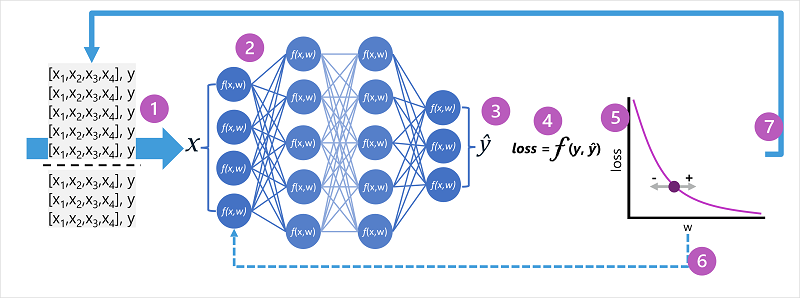
1. Vengono definiti i set di dati di training e di convalida e le funzionalità di training vengono immesse nello strato di input.
2. I neuroni di ogni strato della rete applicano i loro pesi (inizialmente assegnati in modo casuale) e alimentano i dati attraverso la rete.
3. Il livello di output produce un vettore contenente i valori calcolati per ŷ. Ad esempio, un output per una stima della classe pinguino potrebbe essere [0,3. 0.1. 0.6].
4. Una funzione di perdita viene usata per confrontare i valori ŷstimati con i valori y noti e aggregare la differenza ( nota come perdita). Ad esempio, se la classe nota per il caso che ha restituito l'output nel passaggio precedente è Chinstrap, il valore y deve essere [0,0, 0,0, 1,0]. La differenza assoluta tra questo valore e il vettore ŷ è [0.3, 0.1, 0.4]. In realtà, la funzione di perdita calcola la varianza aggregata per più casi e la riepiloga come un singolo valore di perdita.
5. Poiché l'intera rete è essenzialmente una grande funzione annidata, una funzione di ottimizzazione può usare il calcolo differenziale per valutare l'influenza di ogni peso della rete sulla perdita, e determinare come potrebbero essere regolati (in aumento o in diminuzione) per ridurre la quantità di perdita complessiva. La tecnica di ottimizzazione specifica può variare, ma in genere prevede un approccio di discesa del gradiente in cui ogni peso viene aumentato o diminuito per ridurre al minimo la perdita.
6. Le modifiche apportate ai pesi vengono retropropagate agli strati della rete, sostituendo i valori usati in precedenza.
7. Il processo viene ripetuto per più iterazioni (note come epoche) fino a quando la perdita viene ridotta al minimo e il modello esegue la stima in modo sufficientemente accurato.