Schema e algoritmi del profilo del modello di dispositivo a colori WCS

  • Articolo

In questo argomento vengono fornite informazioni sullo schema del profilo del modello di dispositivo wcs color e sui relativi algoritmi associati.

Questo argomento include le sezioni seguenti:

Panoramica

Questo schema viene usato per specificare il contenuto di un profilo del modello di dispositivo a colori (CDMP). Gli algoritmi di base associati sono descritti di seguito.

Lo schema DMP (Device Model Profile) di base è costituito dai dati di misurazione del campionamento.

Il componente di campionamento dello schema XML DMP fornisce il supporto per le destinazioni di misura dei colori di base, concentrandosi su destinazioni standard e destinazioni standard comuni ottimizzate per i modelli di dispositivo di base.

Inoltre, il profilo del dispositivo fornisce informazioni specifiche sul modello di dispositivo di destinazione e fornisce un criterio che il modello di dispositivo di fallback di base può usare se il modello di destinazione non è disponibile. Le istanze del profilo possono includere estensioni private usando meccanismi di estensione XML standard.

Architettura del profilo del modello di dispositivo a colori

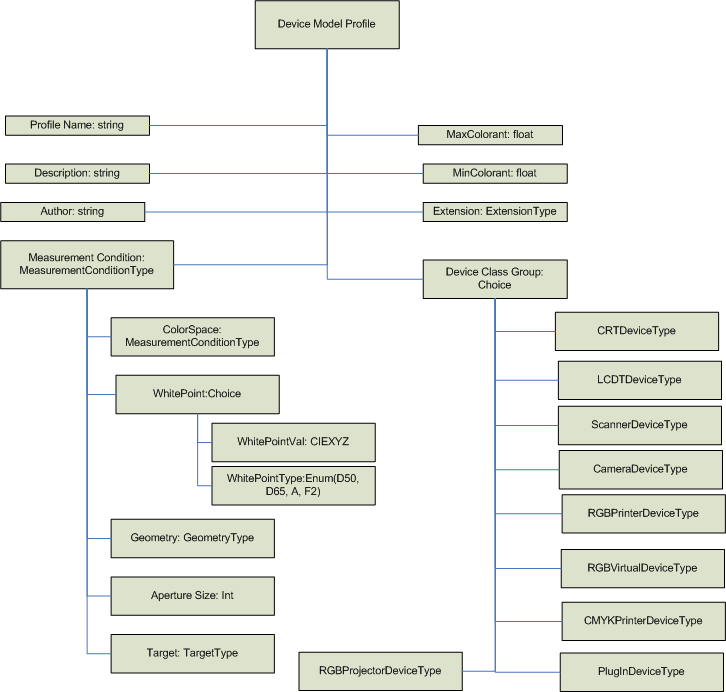
Diagram that shows the information that makes up a Device Model Profile.

The CDMP Schema

<?xml version="1.0" encoding="UTF-8"?>
<xs:schema 
  xmlns:cdm="http://schemas.microsoft.com/windows/2005/02/color/ColorDeviceModel"
  xmlns:wcs="http://schemas.microsoft.com/windows/2005/02/color/WcsCommonProfileTypes"
  targetNamespace="http://schemas.microsoft.com/windows/2005/02/color/ColorDeviceModel"
  xmlns:xs="http://www.w3.org/2001/XMLSchema"
  elementFormDefault="qualified"
  attributeFormDefault="unqualified"
  blockDefault="#all"
  version="1.0">

  <xs:annotation>
    <xs:documentation>
      Color Device Model profile schema.
      Copyright (C) Microsoft. All rights reserved.
    </xs:documentation>
  </xs:annotation>

  <xs:import namespace="http://schemas.microsoft.com/windows/2005/02/color/WcsCommonProfileTypes" />

  <xs:complexType name="RGBType">
    <xs:attribute name="R" type="xs:float" use="required"/>
    <xs:attribute name="G" type="xs:float" use="required"/>
    <xs:attribute name="B" type="xs:float" use="required"/>
  </xs:complexType>

  <xs:complexType name="NonNegativeRGBType">
    <xs:attribute name="R" type="wcs:NonNegativeFloatType" use="required"/>
    <xs:attribute name="G" type="wcs:NonNegativeFloatType" use="required"/>
    <xs:attribute name="B" type="wcs:NonNegativeFloatType" use="required"/>
  </xs:complexType>

  <xs:complexType name="NonNegativeCMYKType">
    <xs:attribute name="C" type="wcs:NonNegativeFloatType" use="required"/>
    <xs:attribute name="M" type="wcs:NonNegativeFloatType" use="required"/>
    <xs:attribute name="Y" type="wcs:NonNegativeFloatType" use="required"/>
    <xs:attribute name="K" type="wcs:NonNegativeFloatType" use="required"/>
  </xs:complexType>
  
  <xs:complexType name="NonNegativeRGBSampleType">
    <xs:sequence>
      <xs:element name="RGB" type="cdm:NonNegativeRGBType"/>
      <xs:element name="CIEXYZ" type="wcs:NonNegativeCIEXYZType"/>
    </xs:sequence>
    <xs:attribute name="Tag" type="xs:string" use="optional"/>
  </xs:complexType>
  
  <xs:complexType name="NonNegativeCMYKSampleType">
    <xs:sequence>
      <xs:element name="CMYK" type="cdm:NonNegativeCMYKType"/>
      <xs:element name="CIEXYZ" type="wcs:NonNegativeCIEXYZType"/>
    </xs:sequence>
    <xs:attribute name="Tag" type="xs:string" use="optional"/>
  </xs:complexType>
  
  <xs:group name="RGBPrimariesGroup">
    <xs:sequence>
      <xs:element name="WhitePrimary" type="wcs:NonNegativeCIEXYZType"/>
      <xs:element name="RedPrimary" type="wcs:NonNegativeCIEXYZType"/>
      <xs:element name="GreenPrimary" type="wcs:NonNegativeCIEXYZType"/>
      <xs:element name="BluePrimary" type="wcs:NonNegativeCIEXYZType"/>
      <xs:element name="BlackPrimary" type="wcs:NonNegativeCIEXYZType"/>
    </xs:sequence>
  </xs:group> 
  
  <xs:complexType name="MeasurementConditionsType">
    <xs:annotation>
      <xs:documentation>
      Optional measurement conditions. 
       
      We only support CIEXYZ for measurement color space in this version. 
      If the white point value from the measurement conditions is not available, 
      the default processing will use
        - "D50" for printer and scanners
        - "D65" for camera and displays.          
      </xs:documentation>
    </xs:annotation>
    <xs:sequence>
      <xs:element name="ColorSpace" minOccurs="0">
        <xs:simpleType>
          <xs:restriction base="xs:string">
            <xs:enumeration value="CIEXYZ"/>
          </xs:restriction>
        </xs:simpleType>    
      </xs:element>
      <xs:choice minOccurs="0">
        <xs:element name="WhitePoint" type="wcs:NonNegativeCIEXYZType"/>
        <xs:element name="WhitePointName">
          <xs:simpleType>
            <xs:restriction base="xs:string">
              <xs:enumeration value="D50"/>
              <xs:enumeration value="D65"/>
              <xs:enumeration value="A"/>
              <xs:enumeration value="F2"/>
            </xs:restriction>
          </xs:simpleType>
        </xs:element>
      </xs:choice>
      <xs:element name="Geometry" minOccurs="0">
        <xs:simpleType>
          <xs:restriction base="xs:string">
            <xs:enumeration value="0/45"/>
            <xs:enumeration value="0/diffuse"/>
            <xs:enumeration value="diffuse/0"/>
            <xs:enumeration value="direct"/>
          </xs:restriction>
        </xs:simpleType>   
      </xs:element>
      <xs:element name="ApertureSize" type="xs:int" minOccurs="0"/>
    </xs:sequence>
  </xs:complexType>
  
  <xs:complexType name="DisplayMeasurementType">
    <xs:sequence>
      <xs:group ref="cdm:RGBPrimariesGroup"/>
      <xs:element name="GrayRamp">
        <xs:complexType>
          <xs:sequence>
            <xs:element name="Sample" type="cdm:NonNegativeRGBSampleType" maxOccurs="4096"/> 
          </xs:sequence>
        </xs:complexType>
      </xs:element>
      <xs:element name="RedRamp">
        <xs:complexType>
          <xs:sequence>
            <xs:element name="Sample" type="cdm:NonNegativeRGBSampleType" maxOccurs="4096"/> 
          </xs:sequence>
        </xs:complexType>
      </xs:element>
      <xs:element name="GreenRamp">
        <xs:complexType>
          <xs:sequence>
            <xs:element name="Sample" type="cdm:NonNegativeRGBSampleType" maxOccurs="4096"/> 
          </xs:sequence>
        </xs:complexType>
      </xs:element>
      <xs:element name="BlueRamp">
        <xs:complexType>
          <xs:sequence>
            <xs:element name="Sample" type="cdm:NonNegativeRGBSampleType" maxOccurs="4096"/> 
          </xs:sequence>
        </xs:complexType>
      </xs:element>
    </xs:sequence>
    <xs:attribute name="TimeStamp" type="xs:dateTime"/>
  </xs:complexType>

  <xs:complexType name="RGBProjectorMeasurementType">
    <xs:sequence>
      <xs:group ref="cdm:RGBPrimariesGroup"/>
      <xs:element name="ColorSamples">
        <xs:complexType>
          <xs:sequence>
            <xs:element name="Sample" type="cdm:NonNegativeRGBSampleType" maxOccurs="unbounded"/> 
          </xs:sequence>
        </xs:complexType>
      </xs:element>
    </xs:sequence>
    <xs:attribute name="TimeStamp" type="xs:dateTime"/>
  </xs:complexType>

  <xs:simpleType name="OneBasedIndex">
    <xs:restriction base="xs:int">
      <xs:minInclusive value="1"/>
    </xs:restriction>
  </xs:simpleType>
    
  <xs:complexType name="RGBCaptureMeasurementType">
    <xs:sequence>
      <xs:element name="PrimaryIndex">
        <xs:complexType>
          <xs:all>
            <xs:element name="White" type="cdm:OneBasedIndex"/>
            <xs:element name="Black" type="cdm:OneBasedIndex" minOccurs="0"/>
            <xs:element name="Red" type="cdm:OneBasedIndex" minOccurs="0"/>
            <xs:element name="Green" type="cdm:OneBasedIndex" minOccurs="0"/>
            <xs:element name="Blue" type="cdm:OneBasedIndex" minOccurs="0"/>
            <xs:element name="Cyan" type="cdm:OneBasedIndex" minOccurs="0"/>
            <xs:element name="Magenta" type="cdm:OneBasedIndex" minOccurs="0"/>
            <xs:element name="Yellow" type="cdm:OneBasedIndex" minOccurs="0"/>
          </xs:all>
        </xs:complexType>
      </xs:element>
      <xs:element name="NeutralIndices">
        <xs:simpleType>
          <xs:list itemType="cdm:OneBasedIndex"/>
        </xs:simpleType>
      </xs:element>
      <xs:element name="ColorSamples">
        <xs:complexType>
          <xs:sequence>
            <xs:element name="Sample" type="cdm:NonNegativeRGBSampleType" maxOccurs="unbounded"/> 
          </xs:sequence>
        </xs:complexType>
      </xs:element>
    </xs:sequence>
    <xs:attribute name="TimeStamp" type="xs:dateTime"/>
  </xs:complexType>

  <xs:complexType name="RGBPrinterMeasurementType">
    <xs:sequence>
      <xs:element name="ColorCube">
        <xs:complexType>
          <xs:sequence>
            <xs:element name="Sample" type="cdm:NonNegativeRGBSampleType" maxOccurs="unbounded"/> 
          </xs:sequence>
        </xs:complexType>
      </xs:element>       
    </xs:sequence>
    <xs:attribute name="TimeStamp" type="xs:dateTime"/>
  </xs:complexType>
  
  <xs:complexType name="CMYKPrinterMeasurementType">
    <xs:sequence>
      <xs:element name="ColorCube">
        <xs:complexType>
          <xs:sequence>
            <xs:element name="Sample" type="cdm:NonNegativeCMYKSampleType" maxOccurs="unbounded"/> 
          </xs:sequence>
        </xs:complexType>
      </xs:element>       
    </xs:sequence>
    <xs:attribute name="TimeStamp" type="xs:dateTime"/>
  </xs:complexType>

  <xs:complexType name="GammaType">
    <xs:attribute name="value" type="wcs:NonNegativeFloatType" use="required"/>
  </xs:complexType>
  
  <xs:complexType name="GammaOffsetGainType">
    <xs:attribute name="Gamma" type="wcs:NonNegativeFloatType" use="required"/>
    <xs:attribute name="Offset" type="wcs:NonNegativeFloatType" use="required"/>
    <xs:attribute name="Gain" type="wcs:NonNegativeFloatType" use="required"/>
  </xs:complexType>

  <xs:complexType name="GammaOffsetGainLinearGainType">
    <xs:attribute name="Gamma" type="wcs:NonNegativeFloatType" use="required"/>
    <xs:attribute name="Offset" type="wcs:NonNegativeFloatType" use="required"/>
    <xs:attribute name="Gain" type="wcs:NonNegativeFloatType" use="required"/>
    <xs:attribute name="LinearGain" type="wcs:NonNegativeFloatType" use="required"/>
    <xs:attribute name="TransitionPoint" type="wcs:NonNegativeFloatType" use="required"/>
  </xs:complexType>
  
  <xs:simpleType name="FloatList">
    <xs:list itemType="xs:float"/>
  </xs:simpleType>

  <xs:complexType name="OneDimensionLutType">
    <xs:sequence>
      <xs:element name="Input" type="cdm:FloatList"/>
      <xs:element name="Output" type="cdm:FloatList"/>
    </xs:sequence>
  </xs:complexType>

  <xs:complexType name="HDRToneResponseCurvesType">
    <xs:sequence>
      <xs:element name="RedTRC" type="cdm:OneDimensionLutType"/>
      <xs:element name="GreenTRC" type="cdm:OneDimensionLutType"/>
      <xs:element name="BlueTRC" type="cdm:OneDimensionLutType"/>
    </xs:sequence>
    <xs:attribute name="TRCLength" use="required">
      <xs:simpleType>
        <xs:restriction base="xs:int">
          <xs:minInclusive value="0" />
        </xs:restriction>
      </xs:simpleType>
    </xs:attribute>
  </xs:complexType>
  
  <xs:complexType name="GamutBoundarySamplesType">
    <xs:sequence>
      <xs:element name="RGB" type="cdm:RGBType" maxOccurs="unbounded"/>
    </xs:sequence>
  </xs:complexType>
  
  <xs:complexType name="RGBVirtualMeasurementType">
    <xs:sequence>
      <xs:element name="MaxColorantUsed" type="xs:float"/>
      <xs:element name="MinColorantUsed" type="xs:float"/>
      <xs:group ref="cdm:RGBPrimariesGroup"/>
      <xs:choice>
        <xs:element name="Gamma" type="cdm:GammaType"/>
        <xs:element name="GammaOffsetGain" type="cdm:GammaOffsetGainType"/>
        <xs:element name="GammaOffsetGainLinearGain" type="cdm:GammaOffsetGainLinearGainType"/>
        <xs:element name="HDRToneResponseCurves" type="cdm:HDRToneResponseCurvesType"/>
      </xs:choice>
      <xs:element name="GamutBoundarySamples" type="cdm:GamutBoundarySamplesType" minOccurs="0"/>
    </xs:sequence>
    <xs:attribute name="TimeStamp" type="xs:dateTime"/>
  </xs:complexType>
  
  <xs:element name="ColorDeviceModel">
    <xs:complexType>
      <xs:sequence>
        <xs:element name="ProfileName" type="wcs:MultiLocalizedTextType"/>
        <xs:element name="Description" type="wcs:MultiLocalizedTextType" minOccurs="0"/>
        <xs:element name="Author" type="wcs:MultiLocalizedTextType" minOccurs="0"/>
        <xs:element name="MeasurementConditions" type="cdm:MeasurementConditionsType" minOccurs="0"/>
        <xs:element name="SelfLuminous" type="xs:boolean" />
        <xs:element name="MaxColorant" type="xs:float"/>
        <xs:element name="MinColorant" type="xs:float"/>
        <xs:choice>
          <xs:element name="CRTDevice">
            <xs:complexType>
              <xs:sequence>
                <xs:element name="MeasurementData" type="cdm:DisplayMeasurementType"/>
              </xs:sequence>
            </xs:complexType>
          </xs:element>
          <xs:element name="LCDDevice">
            <xs:complexType>
              <xs:sequence>
                <xs:element name="MeasurementData" type="cdm:DisplayMeasurementType"/>
              </xs:sequence>
            </xs:complexType>
          </xs:element>
          <xs:element name="RGBProjectorDevice">
            <xs:complexType>
              <xs:sequence>
                <xs:element name="MeasurementData" type="cdm:RGBProjectorMeasurementType"/>
              </xs:sequence>
            </xs:complexType>
          </xs:element>
          <xs:element name="ScannerDevice">
            <xs:complexType>
              <xs:sequence>
                <xs:element name="MeasurementData" type="cdm:RGBCaptureMeasurementType"/>
              </xs:sequence>
            </xs:complexType>
          </xs:element>
          <xs:element name="CameraDevice">
            <xs:complexType>
              <xs:sequence>
                <xs:element name="MeasurementData" type="cdm:RGBCaptureMeasurementType"/>
              </xs:sequence>
            </xs:complexType>
          </xs:element>
          <xs:element name="RGBPrinterDevice">
            <xs:complexType>
              <xs:sequence>
                <xs:element name="MeasurementData" type="cdm:RGBPrinterMeasurementType"/>
              </xs:sequence>
            </xs:complexType>
          </xs:element>
          <xs:element name="CMYKPrinterDevice">
            <xs:complexType>
              <xs:sequence>
                <xs:element name="MeasurementData" type="cdm:CMYKPrinterMeasurementType"/>
              </xs:sequence>
            </xs:complexType>
          </xs:element>
          <xs:element name="RGBVirtualDevice">
            <xs:complexType>
              <xs:sequence>
                <xs:element name="MeasurementData" type="cdm:RGBVirtualMeasurementType"/>
              </xs:sequence>
            </xs:complexType>
          </xs:element>
        </xs:choice>
        <xs:element name="PlugInDevice" minOccurs="0">
          <xs:complexType>
            <xs:sequence>
              <xs:any namespace="##other" processContents="skip"
                minOccurs="0" maxOccurs="unbounded" />
            </xs:sequence>
            <xs:attribute name="GUID" type="wcs:GUIDType" use="required"/>
          </xs:complexType>
        </xs:element>
      </xs:sequence>
      <xs:attribute name="ID" type="xs:string" use="optional" />
    </xs:complexType>
  </xs:element>
</xs:schema>

Aggiunta calibrazione CDMP WCS v2.0

L'elemento ColorDeviceModel dello schema CDMP è stato aggiornato in Windows 7 per includere il nuovo elemento di calibrazione. Di seguito viene illustrata la modifica allo schema CDMP.

  ...
  <xs:element name="ColorDeviceModel">
    <xs:complexType>
      <xs:sequence>
        ...
        <xs:element name="PlugInDevice" minOccurs="0">
             ...
        </xs:element>
        <xs:element name="Calibration" type="cal:Calibration" minOccurs="0"/>
        ...
      <xs:sequence>
    ...
    <xs:complexType>
  ...

Elementi dello schema CDMP

Nota

Le primarie sono campioni primari di rosso, verde, blu, nero e bianco. Una rampa principale è una rampa tonale dalla luminanza minima al valore primario completo. Il numero massimo di voci in una rampa di tono è 4096.

Nota

I DMP sono necessari per avere dati di misura.

ColorDeviceModelProfile

Questo elemento è di tipo ColorDeviceModel.

Condizioni di convalida: ogni sottoelemento viene convalidato dal proprio tipo.

ColorDeviceModel

Questo elemento è una sequenza dei sottoelementi seguenti

  1. Stringa ProfileName,
  2. stringa di descrizione facoltativa,
  3. facoltativa Stringa autore,
  4. MeasurementConditions MeasurementConditionsType facoltativo,
  5. Boolean auto-luminoso,
  6. MaxColorant float,
  7. MinColorant float,
  8. Scelta degli elementi
    1. CRTDevice,
    2. LCDDevice,
    3. RGBProjectorDevice,
    4. ScannerDevice,
    5. Fotocamera Device,
    6. RGBPrinterDevice,
    7. CMYKPrinterDevice,
    8. RGBVirtualDevice,
  9. PlugInDevice,
  10. ExtensionType facoltativo

Condizioni di convalida: ogni sottoelemento viene convalidato dal proprio tipo. Gli elementi secondari stringa hanno un massimo di 10.000 caratteri. Il sottoelemento MaxColorant deve essere maggiore o uguale a zero (0) e maggiore dell'elemento secondario MinColorant. MinColorant può essere negativo.

NamespaceVersion

xmlns:cdm="http://schemas.microsoft.com/windows/2005/02/color/ColorDeviceModel"

targetNamespace="http://schemas.microsoft.com/windows/2005/02/color/ColorDeviceModel"

Versione

Version = "1.0" con Windows Vista.

Condizioni di convalida: qualsiasi valore >di versione 0.1 o <=2.0 è valido per supportare modifiche non di rilievo al formato.

Documentazione

Schema del profilo del modello di dispositivo.

Copyright (C) Microsoft. Tutti i diritti sono riservati.

Elemento CRTDevice

Questo elemento è una sequenza di sottoelementi di un oggetto MeasurementData DisplayMeasurementType.

Condizioni di convalida: ogni sottoelemento viene convalidato dal proprio tipo.

Elemento LCDDevice

Questo elemento è una sequenza di sottoelementi di un oggetto MeasurementData DisplayMeasurementType.

Condizioni di convalida: ogni sottoelemento viene convalidato dal proprio tipo.

Elemento ProiettoreDevice

Questo elemento è una sequenza di sottoelementi di un oggetto MeasurementData RGBProjectorMeasurementType.

Condizioni di convalida: ogni sottoelemento viene convalidato dal proprio tipo.

Elemento ScannerDevice

Questo elemento è una sequenza di sottoelementi di un oggetto MeasurementData RGBCaptureMeasurementType

Condizioni di convalida: ogni sottoelemento viene convalidato dal proprio tipo.

elemento Fotocamera Device

Questo elemento è una sequenza di sottoelementi di un oggetto MeasurementData RGBCaptureMeasurementType

Condizioni di convalida: ogni sottoelemento viene convalidato dal proprio tipo.

Elemento RGBPrinterDevice

Questo elemento è una sequenza di sottoelementi di un oggetto MeasurementData RGBPrinterMeasurementType.

Condizioni di convalida: ogni sottoelemento viene convalidato dal proprio tipo.

Elemento CMYKPrinterDevice

Questo elemento è una sequenza di sottoelementi di un oggetto MeasurementData CMYKPrinterMeasurementType.

Condizioni di convalida: ogni sottoelemento viene convalidato dal proprio tipo.

Elemento RGBVirtualDevice

Questo elemento è una sequenza di sottoelementi di un RGBVirtualMeasurementDataType.

Condizioni di convalida: ogni sottoelemento viene convalidato dal proprio tipo.

PlugInDeviceType

Questo elemento è una sequenza di un GUID GUIDType e di qualsiasi sottoelemento.

Condizioni di convalida: il GUID viene usato per trovare la corrispondenza con il GUID DLL plugin dm. Sono disponibili al massimo 100.000 sottoelementi personalizzati.

RGBVirtualMeasurementType

Questo elemento è una sequenza costituita da

  1. Gruppo RGBPrimariesGroup

  2. Una scelta di

    • Gamma
    • GammaOffsetGain
    • GammaOffsetGainLinearGam
    • Elementi ToneResponseCurves

  4. GamutBoundarySamples GamutBoundarySamplesType facoltativo

  5. TimeStamp dateTime

Condizioni di convalida: ogni sottoelemento di questi tipi ha le proprie condizioni di convalida.

GammaType

Questo elemento è un tipo complesso costituito dall'attributo

  • Gamma NonNegativeFloatType

Condizioni di convalida: da determinare dal feedback del settore.

GammaOffsetGainType

Questo elemento è un tipo complesso costituito dagli attributi

  • Gamma NonNegativeFloatType
  • Offset NonNegativeFloatType
  • Gain NonNegativeFloatType

Condizioni di convalida: da determinare dal feedback del settore.

GammaOffsetGainLinearGainType

Questo elemento è un tipo complesso costituito dagli attributi

  • Gamma NonNegativeFloatType
  • Offset NonNegativeFloatType
  • Gain NonNegativeFloatType
  • LinearGain NonNegativeFloatType
  • TransitionPoint NonNegativeFloatType.

Condizioni di convalida: da determinare dal feedback del settore.

ToneResponseCurvesType

Questo elemento è una sequenza di

  1. RedTRC FloatPairList
  2. GreenTRC FloatPairList
  3. BlueTRC FloatPairList

L'elemento ha anche un attributo TRCLength di tipo unsignedint.

Condizioni di convalida: da determinare dal feedback del settore.

GamutBoundarySamplesType

Questo elemento è una sequenza di RGBTypes.

Condizioni di convalida: attualmente le occorrenze massime non associate devono essere limitate in base al feedback del settore.

FloatPairList

Questo elemento è un semplice tipo di elenco di coppie di float.

Condizioni di convalida: da determinare dal feedback del settore.

CMYKPrinterMeasurementType

Questo elemento è un

  1. sequenza dell'elemento ColorCube costituito da una sequenza di Sample NonNegativeCMYKSampleType

  2. Attributo dateTime timeStamp.

Condizioni di convalida: da determinare dal feedback del settore.

RGBPrinterMeasurementType

Questo elemento è un

  1. sequenza dell'elemento ColorCube costituito da una sequenza di Sample NonNegativeRGBSampleType

  2. Attributo dateTime timeStamp.

Condizioni di convalida: da determinare dal feedback del settore.

RGBCaptureMeasurementType

Questo elemento è una sequenza di

  1. ComplexType PrimaryIndex di

    1. White OneBasedIndex
    2. Facoltativo Nero OneBasedIndex
    3. Facoltativo Red OneBasedIndex
    4. Facoltativo OneBasedIndex verde
    5. Blue OneBasedIndex facoltativo
    6. Facoltativo Cyan OneBasedIndex
    7. Magenta OneBasedIndex facoltativo
    8. Facoltativo Giallo OneBasedIndex

  3. NeutralIndices delle linee di OneBasedIndex

  4. Sequenza ColorSamples di Sample NonNegativeRGBSampleType

L'elemento ha anche un attributo TimeStamp dateTime.

Condizioni di convalida: da determinare dal feedback del settore.

OneBasedIndex

Questo elemento è un tipo semplice di base di restrizione senza segno int con valore minInclusive = "1".

Condizioni di convalida: da determinare dal feedback del settore.

RGBProjectorMeasurementType

Questo elemento è una sequenza di

  1. Gruppo RGBPrimariesGroup
  2. elemento ColorSamples costituito dalla sequenza di Sample NonNegativeRGBSampleType

L'elemento ha anche un attributo TimeStamp dateTime.

Condizioni di convalida: da determinare dal feedback del settore.

DisplayMeasurementType

Questo elemento è una sequenza di

  1. group RGBPrimariesGroup
  2. GrayRamp della sequenza di Sample NonNegativeRGBType
  3. RedRamp della sequenza di Sample NonNegativeRGBType
  4. GreenRamp della sequenza di Sample NonNegativeRGBType
  5. BlueRamp della sequenza di Sample NonNegativeRGBType

L'elemento DisplayMeasurementType ha anche un attributo TimeStamp dateTime.

Condizioni di convalida: da determinare dal feedback del settore.

MeasurementConditionsType

MeasurementConditionsType è una sequenza di sottoelementi che contiene:

  1. Valore di enumerazione stringa con restrizioni ColorSpace di "CIEXYZ"
  2. scelta facoltativa dell'enumerazione stringa WhitePoint NonNegativeXYZType o WhitePointName dei valori D50, D65, A o F2
  3. Geometry GeometryType
  4. ApertureSize integer in millimetri

Le impostazioni predefinite sono:

  1. Stampanti RGB e CMYK:
    1. CIEXYZ MeasurementSpaceType
    2. D50 WhitePointValue
    3. GeometryType 0/45
    4. 10mm ApertureSize
  2. Scanner:
    1. CIEXYZ MeasurementSpaceType
    2. D50 WhitePointValue
    3. GeometryType 0/45
    4. 10mm ApertureSize
  3. Visualizza e dispositivo virtuale RGB:
    1. CIEXYZ MeasurementSpaceType
    2. D65 WhitePointValue
    3. GeometryType 0/45
    4. 10mm ApertureSize
  4. Fotocamera:
    1. CIEXYZ MeasurementSpaceType
    2. D65 WhitePointValue
    3. GeometryType diretto
    4. 10mm ApertureSize

Condizioni di convalida: la convalida di ogni sottoelemento è determinata dalle condizioni di convalida per tali sottoelementi. Se manca un sottoelemento, viene usato il tipo di modello di dispositivo predefinito specifico.

GeometryType

String

Valori di enumerazione:

  • "0/45"
  • "0/diffusa"
  • "diffuse/0"
  • "Diretto"

Condizioni di convalida: qualsiasi valore ad eccezione dei valori di enumerazione elencati non è valido. Queste informazioni non modificheranno il comportamento di elaborazione della linea di base.

RGBPrimariesGroup

Questo elemento è una sequenza di

  1. WhitePrimary NonNegativeXYZType
  2. RedPrimary NonNegativeXYZType
  3. GreenPrimary NonNegativeXYZType
  4. BluePrimary NonNegativeXYZTYpe
  5. BlackPrimary NonNegativeXYZType

Condizioni di convalida: da determinare dal feedback del settore.

NonNegativeCMYKSampleType

Questo elemento è una sequenza di

  1. CMYK NonNegativeCMYKType
  2. CIEXYZ NonNegativeXYZType

L'elemento ha anche una stringa di tag di attributo facoltativa

Condizioni di convalida: da determinare dal feedback del settore.

NonNegativeRGBSampleType

Questo elemento è una sequenza di

  1. RGB NonNegativeRGBType
  2. CIEXYZ NonNegativeXYZType

L'elemento ha anche una stringa di tag di attributo facoltativa

Condizioni di convalida: da determinare dal feedback del settore.

NonNegativeCMYKType

Questo elemento è costituito da attributi

  1. C float
  2. M float
  3. Float Y
  4. K float

Condizioni di convalida: da determinare dal feedback del settore.

NonNegativeRGBType

Questo elemento è costituito da attributi

  1. R float
  2. G float
  3. B float

Condizioni di convalida: da determinare dal feedback del settore.

Extensiontype

L'elemento ExtensionType è una sequenza di qualsiasi tipo di sottoelemento e viene usato per informazioni proprietarie da applicazioni non Microsoft.

Condizioni di convalida: questo elemento è facoltativo. Può essere presente un massimo di 1000 sottoelementi di estensione.

NonNegativeXYZType

L'elemento NonNegativeXYZType è composto da tre elementi I edizione Enterprise E a precisione singola denominati "X", "Y" e "Z". Questi valori sono limitati ai valori di misurazione dei profili DMP. Queste misurazioni possono essere assoluti (non relativi) VALORI riflettenti CIEXYZ 1931 o valori assoluti (non relativi) CIEXYZ 1931 diretti (trasmissive) in candela per unità quadrate a metro.

Condizioni di convalida: solo i valori reali sono validi e i valori di misura CIEXYZ negativi non sono validi. Poiché si tratta di valori assoluti, i valori possono essere maggiori di 1,0f. Un limite ragionevole per qualsiasi valore "X", "Y" o "Z". è impostato arbitrariamente su 10000,0f.

XYZType

L'elemento XYZType è composto da tre valori A virgola mobile I edizione Enterprise E a precisione singola: "X", "Y" e "Z".

Algoritmi di base CDMP

Baseline del modello di dispositivo CRT

Per comprendere questo modello, è necessario considerare sia il processo di caratterizzazione che la modellazione del dispositivo. Nel processo di caratterizzazione, le misurazioni XYZ vengono eseguite per la prima volta sui colori ottenuti riempiendo il buffer di visualizzazione di un dispositivo di visualizzazione CRT. I valori di esempio seguenti generano dati validi per il modello di dispositivo CRT di base:

Rosso: R = 15, 30, 45, 60, 75, 90, 105, 120, 135, 150, 165, 180, 195, 210, 225, 240, 255, G = B = 0

Verde: G = 15, 30, 45, 60, 75, 90, 105, 120, 135, 150, 165, 180, 195, 210, 225, 240, 255, R = B = 0

Blu: B = 15, 30, 45, 60, 75, 90, 105, 120, 135, 150, 165, 180, 195, 210, 225, 240, 255, R = G = 0

Neutrali: R = G= B = 0, 8, 16, 32, 64, 128, 192, 255

È anche possibile usare incrementi diversi da 15 e incrementi non lineari. Ogni rampa rossa, verde, blu e neutra deve contenere almeno tre campioni, ma è consigliabile fornire più campioni. È necessario fornire campioni per il rosso puro, il verde, il blu, il nero e il bianco. Gli esempi non devono essere spaziati in modo uniforme.

Il processo di compilazione della matrice tristimulo è costituito da due passaggi. Prima di tutto, stimare il valore XYZ del punto nero o il flare. Questo passaggio si basa in gran parte sul lavoro di Berns[3] con una funzione obiettivo leggermente modificata per l'ottimizzazione non lineare. In secondo luogo, calcolare la matrice tristimula in base al risultato del passaggio 1 e anche da un calcolo medio su tutte le misurazioni per canale, non solo quello per il conteggio digitale massimo.

Ognuno di questi passaggi contiene procedure dettagliate. Il punto di partenza è la rampa (17 passaggi nell'esempio) per ognuno dei canali R, G e B. Quando le misurazioni XYZ vengono tracciate sul piano xy della cromaticità, nella figura 1 viene mostrata una situazione tipica. Il passaggio uno consiste nel risolvere un problema di ottimizzazione non lineare per trovare il punto nero "più adatto" che ridurrà al minimo la deriva della cromaticità come uno attraversa lungo i canali R, G e B. In base a Berns[3], cerchiamo ( X K,Y K,Z K ) che riduce al minimo la seguente funzione obiettivo:

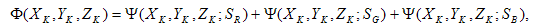
Shows the objective function where Sr, Sg, and Sb are the set of data points on the R, G, and B channels.

dove SR, SG e SB sono il set di punti dati corrispondenti ai punti nei canali R, G e B. Per qualsiasi set S, definire:

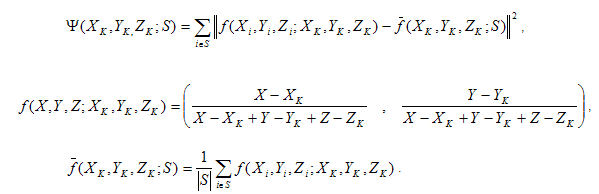
Shows a formula for defining any set S.

Nell'esempio precedente , | S | è la cardinalità di S, ovvero il numero di punti nel set S. 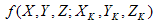Shows a formula for the chromaticity of a point. è le coordinate della cromaticità del punto 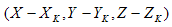Shows a formaula for a point. , quindi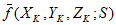Shows a formula for the average or center of mass. , è la media, o centro di massa, di tutti i punti del set S nel piano di cromaticità. Così, 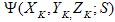Shows a formula for the sum of a second moments of points. è la somma dei secondi momenti dei punti circa il centro di massa ed è una misura di come si distribuiscono i punti sono su di esso. Infine, 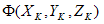Shows a formula for the total measure of the spread of three clusters of points. è una misura totale della distribuzione dei tre cluster di punti circa i rispettivi centri di massa.

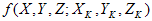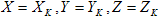Nel calcolo di Shows a formula of f(X,Y,Z; Xk, Yk, Zk). , se Shows a formula for X. , il calcolo viene ignorato e la cardinalità di S viene modificata di conseguenza.

Nonostante la complessità apparente della funzione obiettivo, si tratta di una somma dei quadrati di molte funzioni differenziabili in X K,Y KK (17 punti 2xy -components 3 canali = 102, nell'esempio) e, pertanto, è amenable alle tecniche standard nonlinear least squares, come l'algoritmo Levenberg-Marquardt, che è l'algoritmo usato in WCS. Si noti che la funzione obiettivo precedente è diversa da quella suggerita in Berns[3] in quanto quest'ultima funzione misura la varianza delle distanze dal centro di massa, in modo che la varianza sia zero quando i punti sono equidistanti dal centro della massa, anche se possono estendersi un po ' su di esso. Nell'esempio, la dispersione dei punti viene contollata direttamente utilizzando i secondi momenti.

Come per qualsiasi algoritmo iterativo per il problema dei minimi quadrati non lineari, Levenberg-Marquardt richiede un'ipotesi iniziale. Ci sono due candidati ovvi. Uno è (0, 0, 0); l'altro è il punto nero misurato. Per il CTE, il punto nero misurato viene usato per primo come ipotesi iniziale. Se viene superato un massimo di 100 iterazioni senza raggiungere una soglia di una distanza media pari a 0,001 di ogni punto dal centro della massa (che corrisponde a un valore soglia pari a (0,001) 17 3 = 0,000051 per la funzione obiettivo, viene eseguito un altro round di iterazioni con l'ipotesi iniziale di (0, 0, 0, 0). La stima risultante del punto nero è XYZ confrontata con la stima migliore rispetto al round precedente di iterazioni (con il punto nero misurato come ipotesi iniziale). Usare la stima che fornisce il valore più piccolo per la funzione obiettivo. La scelta di 100 iterazioni e la distanza di errore di 0,001 sono state selezionate empiricamente. Nelle versioni future potrebbe essere ragionevole parametrizzare la distanza dell'errore.

Il risultato del passaggio 1 è il punto nero stimato ( XK,Y K,Z K ). Il passaggio due consiste nel determinare la matrice tristimulale mediando la cromaticità dei punti nei tre cluster ottenuti nel passaggio 1. Per i CRT, questa operazione viene eseguita principalmente per ridurre al minimo gli effetti degli errori di misurazione. I punti usati nella media della cromaticità devono essere gli stessi punti usati nell'ottimizzazione nel passaggio 1. In altre parole, se il primo punto (conteggio digitale 15, nell'esempio) in ogni rampa viene scartato nel passaggio di ottimizzazione, lo stesso deve essere eseguito nella media. Se 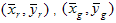Shows formulas of averaged chromaticity for coordinates in the red and green channels. 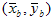e Shows a formula of averaged chromaticity for coordinates in the blue channel. sono le coordinate della cromaticità media dei canali rosso, verde e blu, la procedura seguente determina la matrice tristimula. Prima di tutto, risolvere il sistema lineare 3?3:

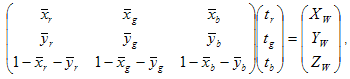
Shows the first part of the procedure to solve a 3?3 linear system.

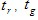
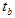
Shows the second part of the 3?3 linear system.Show the t subscript b value at the end of the second part of the 3?3 linear system.

XW,Y W,Z W

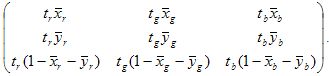
Shows the final part of the procedure to solve a 3?3 linear system.

Dopo aver determinato la matrice tristimulo, la determinazione delle curve di tono segue l'approccio standard. Per la visualizzazione CRT, si presuppone che i singoli canali seguano il modello "GOG":

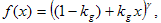
Shows the formula for the 'G O G' model.

dove kg è il "guadagno", 1 -kg è il "offset" e ? è la "gamma". La matrice inversa della matrice tristimulo viene applicata ai dati XYZ dei neutrali per ottenere i dati RGB lineari, che vengono quindi correlati ai valori RGB digitali usando la regressione non lineare nel modello GOG. Queste caratteristiche non devono essere uguali per i canali R, G e B e in genere non sono uguali.

Berns[1]: Berns, Billmeyer e Saltzman's Principles of Color Technology, 3 rd Ed. John Wiley & Sons (2000).

Berns[2]: Berns and Katoh, The digital to radiometric transfer function for computer controlled CRT display, CIE Expert Symposium '97 Color Standards for Imaging Technology, Nov. 1997.

Berns[3]: Berns, Fdevice e Taplin, Stima delle emissioni a livello nero di display controllati da computer, ricerca e applicazione, 28: 379-383 Wiley Periodici, Inc. (2003)

Kang[1]: Kang, Tecnologia dei colori per dispositivi elettronici di imaging, SPIE (1997)

Katoh[1]: Katoh, Deconfiguration e Berns, Una accurata caratterizzazione del monitoraggio CRT (II) per un'estensione al metodo CIE e la sua verifica, Opt. Rev. 8: 397-408 (2001)

Baseline del modello di dispositivo LCD

La baseline del modello di dispositivo LCD è simile alla baseline del modello di dispositivo CRT. Questa sezione illustra i modi in cui la modellazione LCD differisce dalla modellazione CRT.

Una differenza è che non è possibile presupporre che i display LCD seguano il modello GOG usato per i CRT e che le curve di tono vengano ottenute tramite interpolazione di dati misurati. Per questo motivo, l'asse neutro del dispositivo deve essere campionato più frequentemente.

Ecco alcuni valori di esempio tipici che possono generare dati validi per la baseline del modello di dispositivo LCD:

Rosso: R = 15, 30, 45, 60, 75, 90, 105, 120, 135, 150, 165, 180, 195, 210, 225, 240, 255, G = B = 0

Verde: G = 15, 30, 45, 60, 75, 90, 105, 120, 135, 150, 165, 180, 195, 210, 225, 240, 255, R = B = 0

Blu: B = 15, 30, 45, 60, 75, 90, 105, 120, 135, 150, 165, 180, 195, 210, 225, 240, 255, R = G = 0

Neutrali: R = G = B = 0, 15, 30, 45, 60, 75, 90, 105, 120, 135, 150, 165, 180, 195, 210, 225, 240, 255.

Il processo di media delle cromatiche dei colori misurate per ottenere le cromaticità per le primarie del dispositivo è più critico per i LCD di quanto sia per i CRT. Quando le misurazioni XYZ vengono tracciate sul piano xy-chromaticity , viene visualizzata una situazione tipica nella figura 1. Si noti che la cromaticità si allontana verso il punto nero. Ciò è dovuto al fatto che tutti gli LCD hanno una certa quantità di perdita di luce.

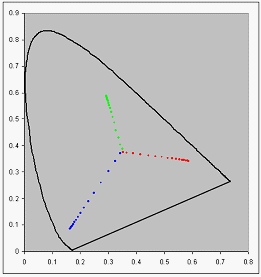
Diagram that shows a graph of the chromaticity using raw data with no correction.

Figura 1 : Diagramma della cromaticità che usa dati non elaborati senza correzione

Quando viene sottratto dalle misurazioni XYZ non elaborate, nella figura 2 viene illustrata una situazione tipica. I punti sono ora raggruppati su tre centri, anche se non cadono in modo identico su di essi. Il processo di media descritto per i CRT migliora notevolmente i risultati per gli LCD.

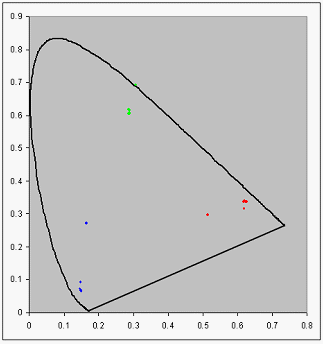
Diagram that shows a graph of the chromaticity using raw data with an adjusted black point.

Figura 2 : Diagramma della cromaticità che usa i dati con punto nero regolato

Baseline del modello di dispositivo di acquisizione RGB

Il modello di dispositivo di acquisizione RGB di base è una sottoclasse della classe IDeviceModel. Nella caratterizzazione colorimetrica dei dispositivi di acquisizione dei colori, ad esempio scanner e fotocamere digitali, viene usato l'approccio seguente. Una destinazione costituita da patch di colore con valori CIEXYZ noti viene acquisita usando il dispositivo di acquisizione. Il risultato dell'acquisizione è un'immagine bitmap RGB in cui il colore di ogni patch viene codificato in un valore RGB. Questi valori RGB del dispositivo sono specifici di un particolare dispositivo di acquisizione. L'obiettivo della caratterizzazione colorimetrica è stabilire una relazione empirica tra i valori RGB del dispositivo e i valori CIEXYZ o una trasformazione matematica da RGB a XYZ che modella il più accuratamente possibile il comportamento del dispositivo di acquisizione.

Una trasformazione matematica di questo tipo può essere modellata ragionevolmente da polinomiali di gradi bassi. Questa procedura è dettagliata nella letteratura, ad esempio Kang[92], Kang[97]. In Kang[97], viene segnalato un approccio che usa un set di tre polinomiali con 3, 6, 8, 9, 11, 14 o 20 termini nelle variabili R, G e B, mentre i tre polinomiali regredisce rispettivamente nei componenti X, Y, Z dello spazio CIEXYZ. Per il polinomio a 20 termini, il formato è:

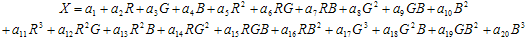
Shows the 20-term polynomial.

Esistono espressioni simili per Y e Z. La tecnica matematica per adattare i polinomiali rientra in "Regressione lineare multivariata" ed è descritta in qualsiasi testo elementare in Statistiche.

Questo metodo di regressione lineare non riduce al minimo la funzione obiettivo "destra". Per impostazione predefinita, la regressione lineare trova la soluzione dei minimi quadrati, il che implica che i coefficienti ottenuti ridurranno al minimo la somma totale dei quadrati di errori nello spazio sottostante, o in modo equivalente, la somma dei quadrati delle distanze euclidee. In pratica, si vuole ridurre al minimo la somma dei quadrati di ? Es, dove ? E è uno degli standard accettati, ad esempio CIE94. Ridurre al minimo questa funzione obiettivo è un problema di regressione non lineare.

Nel nuovo motore, Lab to XYZ è lo spazio colore CIE regredito in e il polinomio cubo a 20 termini viene usato come modello per il dispositivo di acquisizione, o coefficienti ls, come,bs in modo che i polinomiali seguenti riducono al minimo la somma dei quadrati di ? E CIE94 s.

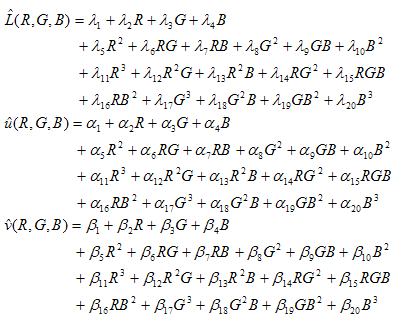
Shows a set of polynomial formulas.

La soluzione ( l, ai, bi ) nello spazio numerico reale 60 dimensionale R203 deve essere tale che l'errore totale seguente sia ridotto al minimo:

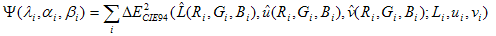
Shows the total error to be minimized.

dove la somma è attraverso tutte le coppie di punti dati (R i,G i,B i;L,u,i,v i ) nel set di dati campionati più punti di controllo aggiuntivi per essere descritti in dettaglio nel codice seguente. Si tratta di un problema di regressione non lineare perché i parametri ?i, ai, * i* immettere nella funzione obiettivo in modo non lineare (non quadraticamente).

Perché la funzione obiettivo ? è una funzione non lineare (e nonquadratica) dei parametri ?i, ie * i*, è necessario ricorrere alle tecniche iterative per risolvere il problema di ottimizzazione. Poiché la forma della funzione obiettivo è una somma di quadrati, viene usata una tecnica di ottimizzazione standard denominata algoritmo Levenberg-Marquardt. È considerato il metodo di scelta per problemi non lineari minimi quadrati. Per gli algoritmi iterativi come Levenberg-Marquardt, è necessario fornire un'ipotesi iniziale. Una buona ipotesi iniziale è in genere fondamentale per trovare il valore minimo corretto. In questo caso, un buon candidato per l'ipotesi iniziale è la soluzione del problema di regressione lineare. Per prima cosa, ridurre al minimo la somma del quadrato delle distanze euclidee nello spazio lab, definendo una funzione obiettivo quadratica:

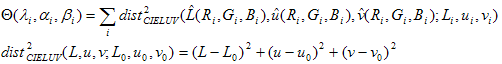
Shows a defined quadratic objective function.

La soluzione matematica a tale problema di "quadrati lineari minimi" è ben nota. Perché ?i compare solo nella modellazione L, uni compare solo nella modellazione u e * i* compare solo nella modellazione v; il problema di ottimizzazione può essere scomposto in tre sottoproblemi: uno per L, uno per u e uno per v. Si considerino le equazioni L . Le equazioni u e le equazioni v seguono esattamente lo stesso argomento. Il problema di ridurre al minimo la somma dei quadrati di errori in L può essere dichiarato come risolvere l'equazione di matrice seguente nel senso meno quadrato:

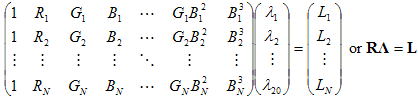
Shows a matrix equation for L.

dove N è il numero totale di punti dati (punti campionati originali più punti di controllo creati in modo descritto di seguito). In genere, N è molto più grande di 20, quindi l'equazione precedente è eccessiva, richiedendo una soluzione minima di quadrati. È disponibile una soluzione di modulo chiuso per ?

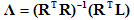
Shows a closed form solution.

In pratica, la valutazione diretta tramite la soluzione di modulo chiusa non viene usata perché presenta proprietà numeriche scarse. Al contrario, alla matrice del coefficiente viene applicato un qualche tipo di algoritmo di fattorizzazione della matrice che riduce il sistema di equazioni a una forma canonica. Nell'implementazione corrente, la scomposizione del valore singolare (SVD) viene applicata alla matrice R e quindi viene risolto il sistema scomposto risultante.

La soluzione al problema di regressione lineare, indicata da 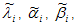Shows the solution to the linear regression problem. , viene usata come punto iniziale dell'algoritmo Levenberg-Marquardt. In questo algoritmo viene calcolato un passaggio di valutazione che dovrebbe avvicinare il punto alla soluzione ottimale. Il passaggio di valutazione soddisfa un set di equazioni lineari dipendenti dal valore funzionale e dai valori dei derivati al punto corrente. Per questo motivo, i derivati della funzione obiettivo ? rispetto ai parametri ?i, sono necessari input per l'algoritmo Levenberg-Marquardt. Anche se sono presenti 60 parametri, è disponibile un collegamento che consente di calcolare molto meno. Per la regola catena di Calculus,

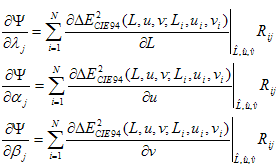
Shows an equation that allows a shortcut using the Chain Rule of Calculus.

dove j = 1, 2, , 20, L,u i,v i sono il valore CIELAB del punto di esempio i e Rij è la voce (i,j )th della matrice R definita in precedenza. Invece di calcolare derivati per 60 parametri, è quindi possibile calcolare derivati per L, a e b usando la differenza numerica in avanti.

È inoltre necessario configurare un criterio di arresto per gli algoritmi iterativi. Nell'implementazione corrente, le iterazioni vengono terminate se il quadrato medio DECIE94 è minore di 1 o il numero di iterazioni eseguite ha superato 10. Il numero 10 deriva dall'esperienza pratica che se le prime iterazioni non riducono significativamente l'errore, ulteriori iterazioni non potrebbero aiutare molto altro che spostare il punto in modo oscillatorio, ovvero l'algoritmo potrebbe non convergere. Anche nel caso in cui l'algoritmo diverga, è possibile assicurarsi che il DECIE94 non sia peggiore di quello che è stato avviato, vale a dire con i parametri ottenuti dalla regressione lineare.

Anche con il metodo precedente di regressione non lineare, esistono diversi problemi con l'adattamento. Un problema è che i polinomiali tendono a superare o superare i punti dati. Nel processo di montaggio possono essere introdotti maxima e minima locali artificiali. Questo può essere contrastato usando polinomiali di basso grado, che è il motivo per cui non si dovrebbe usare più di tre gradi. Un aspetto più serio di overshooting o sottoshooting è che, mentre un polinomio può assumere qualsiasi valore reale teoricamente, lo spazio che cerca di modellare in genere ha vincoli fisici e vincoli pratici. CIEXYZ deve avere tutti i valori X, Y, Z non negativi, ovvero un vincolo fisico. In pratica, prendono valori solo nella grandezza di centinaia, non migliaia o superiori. Analogamente, CIELAB o CIELUV ha propri vincoli fisici e pratici. Quando lo spazio RGB viene riempito sufficientemente con punti di esempio, il problema di sovrashooting o di sottosezioni non è grave. Tuttavia, i punti RGB acquisiti dal dispositivo di acquisizione in genere non riempiono lo spazio RGB in modo uniforme. I punti possono riempire solo l'80% del cubo RGB, o peggio, possono risiedere in una manifold dimensionale inferiore. In questo caso, i polinomi regrediti possono eseguire un lavoro scadente per estrapolare i valori oltre i punti dati, a volte restituendo stime non realistiche. Si vuole un modello che restituisca sempre valori ragionevolmente realistici. Ciò richiede un metodo che possa controllare in modo efficace il comportamento limite dei polinomiali di regressione imponendo costi aggiuntivi a tali polinomiali che si comportano in modo irregolare vicino al limite del cubo RGB. Un'ulteriore misura per garantire che i polinomiali restituiscono sempre valori realistici venga applicato ritagliando l'output a all'interno del locus spettrale CIE.

È a questo punto che la modellazione dello scanner e la modellazione della fotocamera si differenziano tra loro. Il modello di fotocamera dovrebbe estrapolare le aree oltre i punti campionati, tra cui le "evidenziazioni speculari", la stessa estrapolazione non è necessaria per il modello scanner. La destinazione dello scanner dovrebbe coprire una caratterizzazione simile ai materiali stampati da analizzare. Il modello dello scanner è ancora necessario per essere affidabile nel senso che non deve restituire valori non realistici, ma l'estrapolazione molto oltre la destinazione di caratterizzazione non è necessaria. Per garantire la robustezza, il polinomio L-sopra viene ritagliato a 100, ovvero il modello polinomiale viene costretto a estrapolare oltre "Dmin" della destinazione dello scanner.

Il modello di fotocamera dovrebbe estrapolare le evidenziazioni speculari, quindi il ritaglio a 100 è indesiderato. Viene invece usato l'algoritmo seguente.

I punti di controllo artificiali vengono introdotti per controllare il comportamento dei polinomiali nelle aree con campionamento insufficiente. Posizionando in modo strategico questi punti di controllo con valori appropriati, servono a "tirare" i polinomiali nella direzione richiesta. Nell'implementazione corrente vengono usati otto punti di controllo corrispondenti agli angoli del cubo RGB. Se i valori del dispositivo vengono normalizzati in unity, questi punti sono:

R = 0, G = 0, B = 0

R = 0, G = 0, B = 1

R = 0, G = 1, B = 0

R = 0. G = 1, B = 1

R = 1, G = 0, B = 0

R = 1, G = 0, B = 1

R = 1, G = 1, B = 0

R = 1, G = 1, B = 1

Ad eccezione del bianco R G = =B = 1, associato a un valore CIELAB pari a L = 100, u =v = 0, viene usato l'algoritmo di estrapolazione seguente per determinare il valore CIELAB appropriato a cui associare. In genere, per un dato (R,G,B ), un peso è associato a ognuno di essi (R,G i,B i ) nel set di dati campionati. Ci sono due obiettivi per assegnare il peso. In primo luogo, il peso è inversamente proporzionale alla distanza tra (R,G,B ) e (Ri,G i,B i ). In secondo luogo, si vuole eliminare o assegnare peso 0 a, punti con una tonalità diversa rispetto al punto specificato (R,G,B ). Per tenere conto della tonalità, prendere in considerazione i punti che si trovano all'interno di un cono il cui vertice si trova a (0, 0, 0), il cui asse coincide con la linea che unisce (0, 0, 0) a (R,G,B ) e il cui angolo semi verticale ? soddisfa cos ? = 0,9. Vedere la figura 3 per un'illustrazione di questo cono.

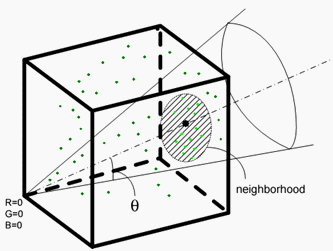
Diagram that shows the shape of the neighborhood.

Figura 3 : Filtro dei punti campione in base all'angolo e alla distanza. La forma del quartiere rappresentato è solo a scopo illustrativo. La forma effettiva dipende dalla distanza utilizzata; è un quartiere a forma di rombo se viene utilizzata la norma 1.

All'interno di questo cono viene eseguito un secondo filtro basato sulla distanza RGB, che usa la norma 1, definita da

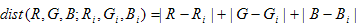
Shows the formula for the second filtering within the cone.

Con il cono corrente, la ricerca iniziale è costituita da punti che si trovano entro una distanza di 0,1 da (R,G,B ). Se non viene trovato alcun punto all'interno di questo raggio, il raggio viene aumentato di 0,1 e la ricerca viene riavviata. Se la rete successiva non punta neanche, il raggio viene aumentato di 0,1. Questo processo continua fino a quando il raggio supera MaxDist/5, dove MaxDist = 3, nel caso di 1 norma. Se non viene trovato alcun punto, il cono viene ingrandito riducendo il cos ? di 0,05, cioè, aumentando l'angolo ? e riavviare l'intero processo con un raggio crescente. Questo processo continua fino a quando non viene trovato un set di punti non vuoto o cos ? raggiunge 0, ovvero il cono si è aperto per diventare un aereo. A questo punto, la ricerca viene riavviata aumentando il raggio, ad eccezione del fatto che la ricerca continua fino a raggiungere MaxDist. Ciò garantisce che, nello scenario peggiore, venga trovato un set di punti non vuoto. L'algoritmo è riepilogato nel diagramma di flusso nella figura 4.

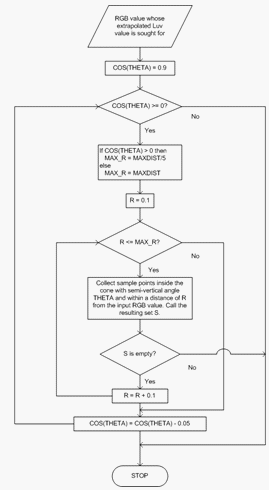
Diagram that shows the flow of the algorithm.

Figura 4 : Diagramma di flusso per determinare il set S di punti di esempio usati nell'estrapolazione per un valore RGB di input

Supponendo che il processo precedente restituisca un set non vuoto S di punti (Ri,G i,B i ) e corrispondente (L,a i,b i ), quindi per ogni punto viene assegnato un peso wi, dato da

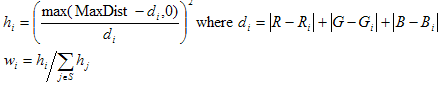
Shows the formula for a weight for each point.

Infine, l'estrapolante è definito da

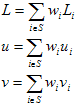
Shows the definition for the extrapolant.

Le equazioni precedenti costituiscono un'istanza dei "metodi ponderati a distanza inversa", comunemente chiamati metodi Shepard. Eseguendo ognuno degli otto punti da eq (6) tramite l'algoritmo, vengono ottenuti otto punti di controllo, ognuno con I valori R,G, B e L,a,b, che vengono inseriti nel pool con i dati di esempio originali.

Per garantire che il modello produa sempre valori di colore validi e per l'integrità del sistema e la stabilità dell'intera pipeline di elaborazione dei colori, è necessario eseguire un ritaglio finale all'output del modello polinomiale. La gamma visiva CIE è descritta dal componente acromatico (Y o L) e dal componente cromatico (xy o a'b', che sono correlati allo spazio XYZ da una trasformazione proiettata). Nell'implementazione corrente, viene usata la cromaticità a 'b' perché è direttamente correlata allo spazio CIELUV. Per qualsiasi valore CIELAB , ritagliare prima L su un valore non negativo:

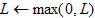
Shows the clipping of L to a non-negative value.

Per consentire l'estrapolazione per le evidenziazioni speculari, L non viene ritagliato a 100, il limite superiore "convenzionale" per L nello spazio lab.

Successivamente, se L = 0, a e b vengono ritagliati in modo che a*= b =* 0. Se L ? 0, calcolare

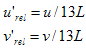
Shows the formula if L=0.

Questi sono i componenti di un vettore nel diagramma a'b' dal punto bianco (u?',v?' ) al colore in questione. Definire il locus spettrale CIE come scafo convesso di tutti i punti (a',b' ), parametrizzato dalla lunghezza d'onda ?:

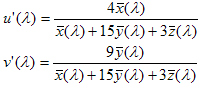
Shows the formula for the wavelength.

dove 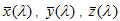Shows the functions for CIE color-matching. sono le funzioni di corrispondenza dei colori CIE per l'osservatore a 2 gradi. Se il vettore si trova all'esterno del locus CIE, il colore viene ritagliato al punto del locus CIE che è l'intersezione del locus e la linea definita dal vettore. Vedere Figura 5. Se si è verificato un ritaglio, il valore a e b viene ricostruito sottraendo prima a?' e b?' dal ritaglio a' e b', quindi moltiplicando per 13 L.

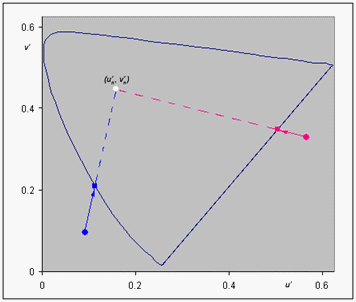
Diagram that shows the graph for the clipping algorithm.

Figura 5 : Algoritmo di ritaglio per i valori lab esterni alla gamma visiva CIE

Nell'implementazione corrente, il locus spettrale CIE nel piano a'b' è rappresentato da una curva lineare a fasi con 35 segmenti (corrispondente a una lunghezza d'onda compresa tra 360 nm e 700 nm inclusi). Ordinando i segmenti di linea in modo che i relativi angoli secondari in corrispondenza del punto bianco siano crescente, che equivale a lunghezze d'onda decrescente, il segmento di linea che interseca con il raggio formato dal vettore precedente può essere trovato da una semplice ricerca binaria.

Baseline del modello di dispositivo della stampante RGB

Una caratterizzazione del dispositivo di una stampante RGB consiste nel costruire un modello empirico del dispositivo che stima il colore CIELUV indipendente dal dispositivo per qualsiasi valore RGB specificato

Esistono due modi per costruire il modello empirico. Un modo consiste nell'usare i dati del dispositivo per una stampante RGB e l'altro consiste nell'usare i dati dei parametri analitici. Nel primo, i dati di misura forniti da un utente per un dispositivo stampante RGB vengono usati per costruire una tabella di ricerca 3D (LUT). I dati di misurazione sono costituiti da valori XYZ per patch RGB campionate in modo uniforme. Le dimensioni di campionamento tipiche sono 9 o 17 per ogni componente. Ogni patch viene misurata con un colorimetro o uno spettrofotometro nello spazio CIEXYZ. Il valore XYZ per una patch viene quindi convertito in valore CIELUV, formando un valore LUT 3D. Nel modello di dispositivo, il metodo di interpolazione tetrahedrale di Sakamoto viene applicato alla LUT 3D per stimare i dati CIELUV per i dati RGB specificati. (Confer US Patent 4275413 (Sakamoto et al.), US Patent 4511989 (Sakamoto), Kang [1]. I due brevetti menzionati sono scaduti. I dati dei parametri analitici passati nel secondo metodo sono semplicemente un valore LUT compilato in precedenza. In genere, tale LUT è stato compilato usando il primo metodo, anche se può essere creato manualmente.

Nella gestione dei colori corrente, la mappa di origine viene definita come mappa che passa dallo spazio RGB a uno spazio di colore CIEXYZ indipendente dal dispositivo. La mappa di destinazione viene definita come mappa che passa dallo spazio dei colori CIEXYZ indipendente dal dispositivo allo spazio RGB. È l'inverso della mappa di origine.

Il modello empirico viene usato direttamente nella mappa di origine. Esegue prima il mapping di un dato dato dati RGB in dati CIELUV, che vengono convertiti in dati XYZ. Nella mappa di destinazione i dati CIEXYZ indipendenti dal dispositivo vengono prima convertiti in dati CIELUV. Vengono quindi usati il modello empirico e il metodo classico Newton-Raphson per stimare i dati RGB migliori per i dati CIELUV. I dettagli sulla conversione da CieLUV a dati RGB sono i seguenti:

Dopo aver generato una LUT 3D da RGB a CieLUV, la mappa da RGB a LUV viene compilata usando l'interpolazione del tetrahedrale su RGB. Questa mappa è indicata dalle equazioni seguenti:

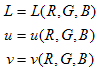
Shows the equations for the map from R G B to L U V.

L'inversione della mappa consiste nel risolvere, per qualsiasi colore 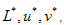Shows L U V. , il sistema seguente di equazioni non lineari:

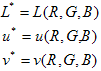
Shows the nonlinear equations for lolving any color L U V.

Nella nuova CTE viene usata un'equazione non lineare basata sul metodo Newton-Raphson classico. Un'ipotesi iniziale, o una precedente, s precedente -(R 0, G 0, B 0 ) viene ottenuta eseguendo una ricerca in una "matrice di inizializzazione" costituita da una griglia uniforme 8x8x8 di coppie precalconate (RGB,Luv). Viene scelto il Luv corrispondente RGB più vicino a L*u*v*. Ogni punto della matrice di inizializzazione corrisponde al centro di una cella in modo che le iterazioni non inizino con un punto sulla faccia limite del cubo RGB. In altre parole, l'RGB dei semi è definito da: STEP = 1/8 s ijk = (STEP/2 + (i-1) STEP, STEP/2+(j-1)STEP, STEP/2+(k-1)STEP) con i,j,k = 1...8 Al passaggio i di Newton-Raphson, la stima 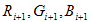Shows the variables for the next estimate. successiva viene ottenuta dalla formula:

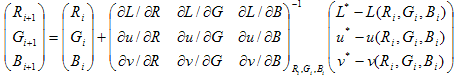
Shows the formula for the estimate.

L'iterazione si arresta quando l'errore (distanza nello spazio CIELUV) è minore di un livello di tolleranza preimpostati (0,1 nel CTE) o quando il numero di iterazioni ha superato il numero massimo consentito di iterazioni (10 nel CTE). I valori per la tolleranza e il numero di iterazioni sono stati determinati empiricamente in modo efficace. Nelle versioni future è possibile modificare il valore di tolleranza.

La matrice jacobiana viene calcolata usando la differenza in avanti, ad eccezione di un punto limite (uno o più di R, G, B è 1) in cui viene usata la differenza all'indietro. Invece di calcolare l'inverso della matrice jacobiana, il sistema lineare viene risolto direttamente usando l'eliminazione gauss-Jordan con pivot completo.

Alla fine delle iterazioni, la convergenza potrebbe comunque non essere ottenuta perché Newton-Raphson è un algoritmo "locale", ovvero funziona bene solo se si inizia con un'ipotesi iniziale vicina alla vera soluzione. Se, alla fine delle iterazioni Newton-Raphson, la convergenza all'interno della tolleranza di errore predefinita non è stata raggiunta, le iterazioni vengono riavviate con un nuovo set di semi, definito come segue.

Ad esempio, la soluzione migliore ottenuta finora è (r, g, b). Da questa soluzione vengono derivati n semi posteriori, dove N = 4. Intuitivamente, la soluzione viene spostata "verso il centro" in una dimensione di passaggio che dipende da N. Vedere la figura 6.

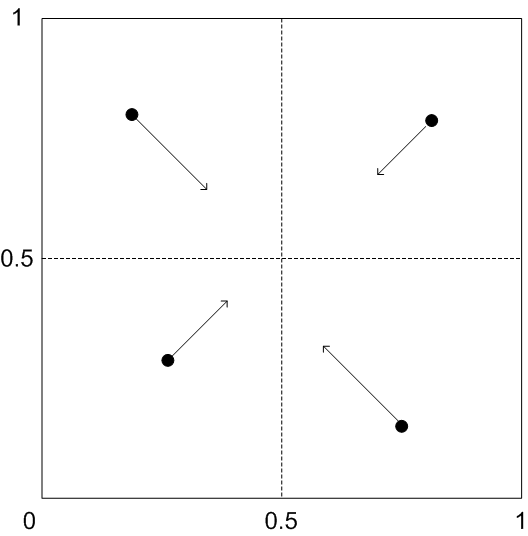
Diagram that shows perturbation directions of the solution.

Figura 6 : Direzione di perturbazione della soluzione dipende dall'ottante in cui si trova.

In altre parole, se r > 0,5, il valore sul canale R viene ridotto, in caso contrario il valore viene aumentato. Esiste una logica simile per i canali G e B. Le definizioni precise sono:

PERTURBATION = 0,5/(N+1)

Dir(r) = -1 se r > 0,5; +1 in caso contrario. Analogamente per Dir(g) e Dir(b)

Il seme jth a posteriori, s ????, è (r + Dir(r) *j * PERTURBATION, g + Dir(g) * j * PERTURBATION, b + Dir(b) * j * PERTURBATION)

Provare la prima ???? e se fornisce una nuova soluzione entro la tolleranza di errore, è possibile arrestarla. In caso contrario, provare il secondo ???? e così via fino al N° ????.

Gli schemi dell'intero algoritmo sono illustrati nella figura 7.

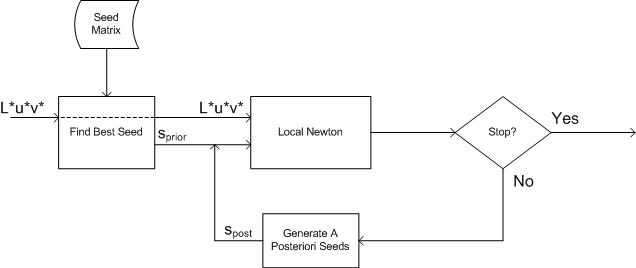
Diagram that shows the flow for inverting the device model.

Figura 7 : Schemi di inversione del modello di dispositivo

Baseline del modello di dispositivo virtuale RGB

Questo modello di dispositivo (DM) è un semplice algoritmo di riproduzione matrice/tono. La matrice è derivata dal punto bianco e dalle primarie usando algoritmi standard di analisi scientifica dei colori. La curva di riproduzione del tono deriva dai parametri di misura in base alle descrizioni ICC di CurveType e ParametricType (o invertite come richiesto). I dettagli degli algoritmi interni verranno forniti dopo la convalida aggiuntiva di problemi di intervallo dinamico elevato.

Il modello di dispositivo virtuale RGB è una curva RGB di riproduzione matrice/tono idealizzata simile alla progettazione del profilo basato su matrice a tre componenti ICC. I parametri di "misurazione virtuale" del DM includono un valore punto bianco (CIEXYZ assoluto), valori primari RGB (CIEXYZ assoluti) e una curva di riproduzione del tono basata su ICC ParametricCurveType e CurveType nella formattazione XML coerente con gli schemi DMP.

La codifica del tipo di funzione ICC parametricCurveType e il supporto corrispondente in IRGBVirtualDeviceModelBase sono illustrati nella tabella seguente.

Tipo di funzione Parametri Type Nota
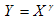Shows the 'GammaType' function.
 g
 GammaType
 Implementazione comune
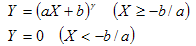Shows the 'GammaOffsetGainType' function.
 ga b
 GammaOffsetGainType
 CIE 122-1966
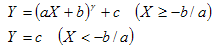Shows the 'GammaOffsetGainOffsetType' function.
 ga b c
 GammaOffsetGainOffsetType
 IEC 61966-3
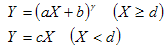Shows the 'GammaOffsetGainGainType' function.
 ga b c d
 GammaOffsetGainGainType
 IEC 61966-2.1
(sRGB)
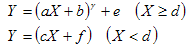Shows a function for 'g a b c d e f' parameters.
 ga b c d e f
 N/D
 Non supportato in WCS

La curva del tono per i dispositivi virtuali RGB viene applicata in DeviceToColorimetric tra i dati di input, pDeviceColors e la moltiplicazione della matrice. Per ColorimetricToDevice, è necessario usare un metodo per invertire la curva del tono. Nell'implementazione di base, questa operazione viene eseguita dall'interpolazione diretta nella stessa curva del tono usata per DeviceToColorimetric.

Le curve devono essere specificate nei profili come coppie di numeri nello spazio float. Il primo numero rappresenta i valori in pDeviceColors. Il secondo numero rappresenta l'output della curva del tono. Tutti i valori nella curva del tono devono essere compresi tra minColorantUsed e maxColorantUsed. Le curve del tono devono contenere almeno due voci: una per minColorantUsed e una per maxColorantUsed. Il numero massimo di voci in ToneCurve è 2048. In generale, più voci nella tabella, più accuratamente è possibile modellare la curvatura. Viene eseguita un'interpolazione lineare a fasi tra le voci.

È possibile considerare metodi di interpolazione alternativi. Se si conosce qualcosa sul comportamento sottostante del dispositivo, è possibile usare meno campioni e modellare in modo più accurato con una curva di ordine superiore. Ma se usi il tipo di curva sbagliato, sarai molto impreciso. Senza altre informazioni, non è possibile indovinare il tipo di curva. Usare quindi l'interpolazione lineare e fornire molti punti dati.

Baseline del modello di dispositivo della stampante CMYK

Una caratterizzazione del dispositivo di una stampante CMYK consiste nel costruire un modello empirico del dispositivo che stima il colore stampato per qualsiasi valore CMYK specificato. La caratterizzazione include anche l'inversione di questo modello in modo che sia possibile fornire una prescrizione del valore CMYK per un determinato colore da stampare. Questo valore viene in genere definito in termini di valore CIEXYZ o CIELAB.

In genere, viene usata una destinazione IT8.7/3 contenente patch CMYK. Le patch sono costituite dal campionamento dello spazio CMYK in modo ben definito in modo che venga formata una griglia rettangolare (con spaziatura non uniforme in C, M, Y e K). Ogni patch viene quindi misurata con un colorimetro o uno spettrofotometro. Le misurazioni nei valori CIEXYZ formano quindi una tabella di ricerca (LUT), da cui viene creato un modello empirico della stampante usando il metodo di interpolazione di Sakamoto. US Patent 4275413 (Sakamoto et al.), US Patent 4511989 (Sakamoto), Kang [1]. I due brevetti menzionati sono scaduti.

I requisiti specifici per i campioni di misurazione CMYK necessari per accettare un profilo del modello di dispositivo come valido dal modello di dispositivo di base della stampante CMYK sono i seguenti. Il set di esempio è descritto più chiaramente come un set di cubi di esempio CMY, ognuno associato a un livello K specifico.

  • È necessario specificare almeno cubi CMY validi per i livelli K = 0 e K = 100.

  • I livelli intermedi K possono essere spaziati in modo non uniforme.

  • Qualsiasi livello K intermedio senza un cubo CMY valido verrà ignorato.

  • I cubi CMY possono usare intervalli di campionamento non uniformi (spaziatura griglia), ma lo stesso set di intervalli di campioni deve essere usato in tutte le dimensioni C,M e Y nel cubo CMY per un determinato livello K.

  • Ogni cubo CMY di livello K può usare un numero e una spaziatura diversi di intervalli di esempio.

  • Tutti i cubi CMY devono contenere gli "angoli" del cubo CMY, ovvero campioni CMY in [0,0,0], [0,0,100], [0,100,0], [100,0,0], [0,100,100], [100,0,100], [100,100, 0], [100,100,100].

  • Tutti i livelli intermedi della griglia CMY devono essere campionati completamente in ogni canale. In altre parole, un esempio deve esistere in ogni intersezione griglia 3D all'interno del cubo CMY.

  • Per i cubi K = 0 e K = 100 CMY, i cubi "solo angoli" 2x2x2 sono il minimo accettato come valido.

    [NOTA: per K=0 e K=100 livelli, un cubo CMY 3x3x3 verrà elaborato come cubo "solo angoli" 2x2x2; il livello di esempio intermedio viene ignorato. 4x4x4 e cubi più grandi avranno tutti gli esempi su griglia usati.]

  • Per i livelli intermedi K, i cubi CMY 4x4x4 sono il minimo accettato come valido.

Un profilo di alta qualità userà griglie di campionamento più fine rispetto al minimo richiesto per la validità, in genere 9x9x9x9 o superiore. Gli esempi delle destinazioni IT8.7/3, IT8.7/4 e ECI producono profili di modello di dispositivo validi per il modello di base della stampante CMYK. Anche se questo modello di dispositivo è in grado di ignorare gli esempi estranei (fuori griglia) in queste destinazioni, non è garantito che sia in grado di farlo per altre destinazioni e quindi, è consigliabile rimuovere campioni estranei dai set di misurazioni che entrano nei profili per questo modello di dispositivo.

L'inversione del modello di stampante presenta più difficoltà. Dato un colore di input in CIECAM, c'è una domanda se questo colore si trova all'interno della gamma della stampante. C'è anche il problema relativo alla disposizione dei punti nello spazio di aspetto del colore. Anche se è possibile disporre i valori CMYK per cadere su una griglia rettangolare, come avviee nella destinazione IT8.7/3, lo stesso non può essere detto dei colori stampati risultanti come si trovano nello spazio di aspetto del colore. In generale, vengono sparsi nello spazio di aspetto del colore senza motivo particolare.

Esistono in genere due approcci al problema di inversione dei punti sparsi. Un approccio consiste nell'usare una suddivisione geometrica del gamut della stampante usando solidi elementari tridimensionali, ad esempio tetrahedra. Una suddivisione della gamma della stampante nello spazio di aspetto dei colori può essere indotta dalla suddivisione corrispondente dello spazio CMY(K), vedere Hung[93], Kang[97]. Questo approccio offre il vantaggio della semplicità di calcolo. Nel caso di un tetraedro, vengono usati solo quattro punti in un'interpolazione. D'altra parte, il risultato dipende molto da alcuni punti, il che significa che un errore di misurazione avrà un effetto significativo sul risultato. Anche l'interpolante tende a non essere uniforme. Il secondo approccio non presuppone alcuna suddivisione e si basa sulla tecnica dell'interpolazione dei dati a dispersione. Un esempio classico è la tecnica dell'interpolazione Shepard o del metodo ponderato inverso (vedere Shepard [68]). In questo caso, diversi punti che circondano il punto di input vengono scelti in qualche modo, ognuno assegnato un peso, in genere inversamente proporzionale alla distanza, e l'interpolante viene preso come media ponderata dei punti adiacenti. In questo approccio, la scelta dei punti adiacenti è fondamentale per le prestazioni. Anche se un numero eccessivo di punti può rendere impreciso e non uniforme l'interpolazione, troppi punti impongono un costo di calcolo elevato, poiché i pesi sono in genere funzioni non lineari e costose da calcolare.

I due approcci descritti in precedenza presentano entrambi problemi. L'approccio alla suddivisione dipende in modo critico dai dati ragionevolmente void di rumore e in genere l'interpolante non è molto uniforme. L'interpolazione dei dati a dispersione è più tollerante per il rumore dei dati e in genere offre un interpolatore più uniforme, ma è più costoso dal livello di calcolo.

Il nuovo CTE adotta un approccio alternativo. Il dispositivo CMYK viene considerato come una raccolta di diversi dispositivi CMY, ognuno dei quali ha un valore specifico di nero (K). Utilizzando un algoritmo di selezione che accetta come parametri leggerezza e cromatica, viene scelto un livello di nero. I valori CMY vengono ottenuti inversione della tabella CMY corrispondente alla tabella Luv usando i metodi Newton utilizzati altrove dall'algoritmo della stampante RGB.

Segui questa procedura.

  1. Stampare la destinazione di caratterizzazione, ovvero la destinazione IT8.7/3 o una destinazione contenente il campionamento dello spazio CMYK a intervalli regolari o irregolari.
  2. Misurare la destinazione usando uno spettrofotometro e convertire le misurazioni nello spazio CIELUV.
  3. Costruire la mappa in avanti da CMYK a Luv.
  4. Usare la mappa in avanti per costruire un set di mappe CMY a Luv per un intervallo di valori K.
  5. Per qualsiasi valore Luv di input, il valore CMYK corrispondente viene ottenuto selezionando una delle mappe costruite nel passaggio 4 precedente e invertendo usando il metodo di Newton per ottenere un set di colori CMY per accompagnare il valore K selezionato.

I passaggi 1 e 2, che sono procedure standard, vengono eseguiti da un programma di profilatura che non fa parte del nuovo CTE. La destinazione IT8.7/3 contiene un campionamento ragionevolmente dettagliato di tutti i valori CMYK a vari livelli di C, M, Y e K. In alternativa, è possibile usare una destinazione personalizzata con campionamento uniforme dei canali C, M, Y e K. Dopo la stampa della destinazione, è possibile usare uno spettrofotometro o un colorimetro per misurare il valore XYZ di ogni patch e il valore XYZ può essere convertito nel valore Luv usando il modello CIELUV.

Il passaggio 3, la costruzione della mappa in avanti da CMYK a Luv, può essere ottenuta applicando qualsiasi tecnica di interpolazione nota, ad esempio il metodo tetrahedral o multilineare, sulla griglia rettangolare nello spazio CMYK. Nella nuova CTE viene usata un'interpolazione tetrahedrale 4-dimensionale. Poiché le griglie di campionamento CMY sono in genere diverse in ogni livello di K, tuttavia, viene usata una tecnica di super campionamento, come descritto di seguito. Per un determinato punto CMYK, i livelli K sandwiching vengono prima determinati in base al valore K. Introdurre quindi una "super-griglia" in ogni livello K che è un'unione delle griglie CMY su ognuno dei due livelli K. In ogni livello K, il valore Luv di qualsiasi punto griglia appena introdotto viene ottenuto da un'interpolazione di tetrahedrale tridimensionale all'interno di tale livello K. Infine, viene eseguita un'interpolazione quadridimensionale 4-dimensionale per il punto CMYK specifico in questa nuova griglia.

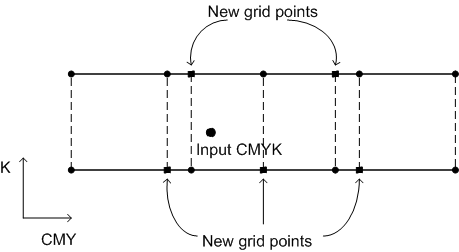
Diagram that shows supersampling.

Figura 8 : Supercampionamento

Il passaggio 4 crea un set di tabelle di ricerca da CMY a Luv (LUT). La mappa in avanti costruita nel passaggio 3 viene chiamata ripetutamente per ricampionare lo spazio CMYK. Lo spazio dei colori CMYK viene campionato usando una spaziatura uniforme di K e un diverso, ma ancora distanziato uniformemente, campionamento di CMY.

Il passaggio 5 è una procedura per ottenere il valore CMYK usando le unità LOGICHE costruite nel passaggio 4 per qualsiasi punto Luv di input. Il valore appropriato di K viene scelto analizzando la leggerezza e il grado di colore nel Luv richiesto. Dopo aver selezionato la tabella, i valori CMY vengono ottenuti dalla tabella usando il metodo di Newton (come documentato in precedenza nel modello di dispositivo della stampante RGB).

Lo spazio CIELUV viene usato nel modello di stampante invece di CIEJab perché il modello di dispositivo deve essere basato esclusivamente sui dati colorimetrici disponibili nel DMP. Il DMP contiene dati colorimetrici per ogni patch misurata, incluso il punto bianco multimediale, quindi è possibile convertire i dati CIEXYZ in dati CIELUV. Tuttavia, non è possibile eseguire la conversione in CIECAM02 JCh o Jab, perché non vi è accesso alle informazioni sulla condizione di visualizzazione nel DMP.

Baseline del modello di dispositivo proiettore RGB

Nota: molti proiettori RGB hanno più di una modalità operativa. In una modalità, che è spesso l'impostazione predefinita e potrebbe essere chiamata qualcosa come "presentazione", la risposta del colore del proiettore è ottimizzata per la massima luminosità. Tuttavia, in questa modalità, il proiettore perde la capacità di riprodurre la luce, colori leggermente cromatici come giallo pallido e alcuni toni di carne. In un'altra modalità, spesso chiamata "film", "video" o "sRGB", il proiettore è ottimizzato per la riproduzione di immagini realistiche e scene naturali. In questa modalità, la luminosità massima viene scambiata per migliorare la qualità complessiva della riproduzione del colore. Per ottenere una riproduzione di colori soddisfacente con proiettori RGB, è necessario posizionare il proiettore in una modalità in cui una gamma uniforme di colori può essere riprodotta.

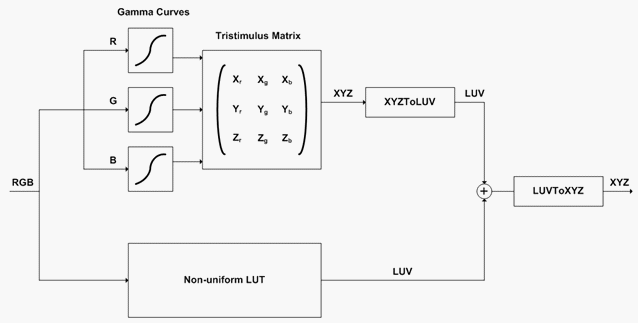
Diagram that shows a D L P device model.

Figura 9 : Modello di dispositivo DLP

Un valore RGB in ingresso passa attraverso due percorsi di calcolo. Il primo è il modello matrice, che restituisce un valore XYZ. Questo è immediatamente seguito dalla conversione da XYZ a Luv. Il secondo è l'interpolazione LUT non uniforme usando l'interpolazione tetrahedrale. L'output dell'interpolazione è già nello spazio Luv per costruzione. I due output vengono aggiunti per ottenere il valore Luv stimato. Questa operazione viene infine convertita in XYZ, ovvero l'output previsto del modello colorimetrico per il dispositivo DLP.

Poiché i proiettori sono dispositivi di visualizzazione, supportano anche l'inversione del modello, ovvero la trasformazione da XYZ a RGB. Poiché il modello di dispositivo trasforma lo spazio RGB nello spazio XYZ, che sono entrambi tridimensionali, l'inversione equivale a risolvere tre equazioni non lineari in tre sconosciute. Questa operazione può essere eseguita tramite tecniche di risoluzione delle equazioni standard, ad esempio Newton-Raphson. È tuttavia preferibile convertire prima XYZ in Luv e quindi invertire la trasformazione Luv In RGB, perché lo spazio Luv è più lineare rispetto allo spazio XYZ.

Baseline del modello di dispositivo ICC

L'interoperabilità del flusso di lavoro CITE ICC è abilitata creando un profilo di modello di dispositivo di base del dispositivo ICC speciale che archivia l'oggetto profilo e crea una trasformazione ICC usando un profilo XYZ no-op. Questa trasformazione viene quindi usata per traslare i colori del dispositivo e CIEXYZ.

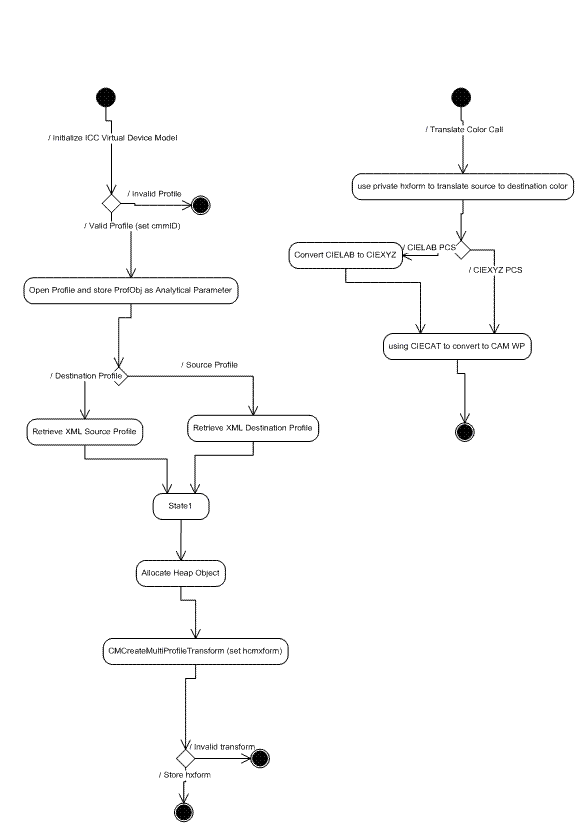
Diagram that shows the C I T E I C C Workflow Interoperability.

Figura 10 : Interoperabilità del flusso di lavoro CITE ICC

Concetti di base sulla gestione dei colori

Schemi e algoritmi di Sistema colori Windows