付録: マトリックス変換
このトピックでは、2-D グラフィックスの行列変換の数学的な概要について説明します。 ただし、Direct2D で変換を使用するために行列演算を知る必要はありません。 数学に興味がある場合は、このトピックをお読みください。それ以外の場合は、このトピックをスキップしてください。
マトリックスの概要
行列は、実数の四角形の配列です。 マトリックスの 順序 は、行と列の数です。 たとえば、マトリックスに 3 つの行と 2 つの列がある場合、順序は 3 × 2 になります。 マトリックスは通常、角かっこで囲まれたマトリックス要素で示されます。
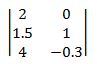
表記: 行列は大文字で指定されます。 要素は小文字で指定されます。 添字は、要素の行番号と列番号を示します。 たとえば、ij は行列 A の i 番目の行と j 番目の列にある要素です。
次の図は、i × j 行列と、マトリックスの各セル内の個々の要素を示しています。

マトリックス演算
このセクションでは、マトリックスで定義される基本的な操作について説明します。
追加。 2 つの行列の合計 A + B は、A と B の対応する要素を追加することによって取得されます。
- A + B = \[ a*ij* \] + \[ b*ij* \] = \[ a*ij* + b*ij* \]
スカラー乗算。 この演算では、行列に実数を乗算します。 実数 k を指定すると、スカラー積 kA は、A のすべての要素に k を乗算して取得されます。
- kA = k\[ a*ij* \] = \[ k × a*ij* \]
行列乗算。 順序 (m × n) と (n × p) の 2 つの行列 A と B を指定すると、積 C = A × B は次のように定義された順序 (m × p) の行列です。
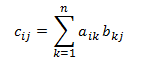
または、同じ方法で次の手順を実行します。
- c*ij* = a*i*1 x b1*j* + a*i*2 x b2*j* + ... + a*in* + b*nj*
つまり、各要素 cij を計算するには、次の操作を行います。
- A の i 番目の行と B の j 番目の列を取ります。
- 行と列の各要素のペアを乗算します。最初の行エントリと最初の列エントリ、2 番目の行エントリ、2 番目の列エントリなどです。
- 結果を合計します。
(2 × 2) 行列と (2 × 3) 行列を乗算する例を次に示します。
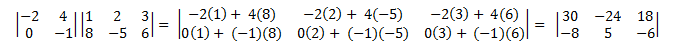
行列乗算は可換ではありません。 つまり、A × B ≠ B × A です。また、定義から、すべての行列のペアを乗算できるわけではないことに従います。 左側の行列の列数は、右側の行列の行数と等しい必要があります。 それ以外の場合、×演算子は定義されていません。
マトリックスを識別します。 ID 行列 (指定された I) は、次のように定義された正方形の行列です。
- *i* = *j* の場合は I*ij* = 1、それ以外の場合は 0。
言い換えると、ID マトリックスには、行番号が列番号と等しい要素ごとに 1 が含まれており、他のすべての要素には 0 が含まれます。 たとえば、3 × 3 つの ID 行列を次に示します。
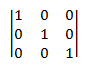
次の等値は、任意の行列 M に対して保持されます。
- M x I = M I x M = M
アフィン変換
アフィン変換は、ある座標空間を別の座標空間にマップする数学的演算です。 つまり、1 つのポイントセットを別のポイントセットにマップします。 アフィン変換には、コンピューター グラフィックスで役立ついくつかの機能があります。
- アフィン変換は 共線性を保持します。 3 つ以上の点が 1 つの線に当てはまる場合でも、変換後に線が形成されます。 直線は直線のままです。
- 2つのアフィン変換の合成はアフィン変換である。
2-D 空間のアフィン変換の形式は次のとおりです。
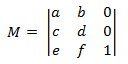
前に指定した行列乗算の定義を適用すると、2 つのアフィン変換の積が別のアフィン変換であることを示すことができます。 アフィン変換を使用して 2D ポイントを変換するには、その点は 1 × 3 行列として表されます。
- P = \|x y 1 \|
最初の 2 つの要素には、点の x 座標と y 座標が含まれています。 1 は 3 番目の要素に配置され、数学が正しく機能します。 変換を適用するには、次のように 2 つの行列を乗算します。
- P' = P × M
これにより、次のように拡張されます。
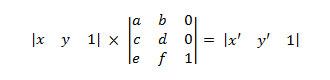
where
- x' = ax + cy + e y' = bx + dy + f
変換されたポイントを取得するには、行列 P' の最初の 2 つの要素を取得します。
- p = (x', y') = (ax + cy + e, bx + dy + f)
Note
1 × n 個の行列は 、行ベクトルと呼ばれます。 Direct2D と Direct3D の両方で行ベクトルを使用して、2D 空間または 3D 空間内のポイントを表します。 列ベクトル (n × 1) を使用し、変換行列を入れ替えることで、同等の結果を得ることができます。 ほとんどのグラフィックス テキストでは、列ベクトル形式が使用されます。 このトピックでは、Direct2D と Direct3D との一貫性を保つ行ベクトル 形式について説明します。
次のいくつかのセクションでは、基本的な変換を派生させます。
変換変換
変換変換マトリックスの形式は次のとおりです。
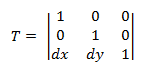
ポイント P をこの数式に接続すると、次の結果が得られます。
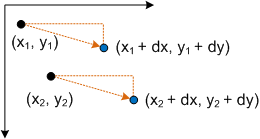
- P' = (*x* + *dx*, *y* + *dy*)
これは、X 軸の dx によって平行移動された点 (x、y) に対応し、Y 軸では dy になります。
スケーリング変換
スケーリング変換マトリックスの形式は次のとおりです。
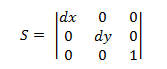
ポイント P をこの数式に接続すると、次の結果が得られます。
- P' = (*x* ≦ *dx*, *y* ≦ *dy*)
dx とdy でスケーリングされたポイント (x、y) に対応します。

原点の周りの回転
原点を中心に点を回転させる行列は、次の形式になります。
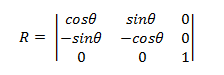
変換されたポイントは次のとおりです。
- P' = (*x*cosΘ – ysinΘ, *x*sinΘ + *y*cosΘ)
証拠。 P' が回転を表していることを示すには、次の図を考えてみましょう。
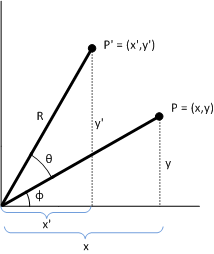
たとえば、以下のように指定したとします。
-
P = (x,y)
-
変換する元のポイント。
-
Φ
-
線(0,0)によって形成される角度をPとする。
-
Θ
-
原点を回転させる角度 (x,y)。
-
P' = (x',y')
-
変換されたポイント。
-
R
-
行の長さ (0,0) から P。回転の円の半径も指定します。
Note
この図では、正の y 軸が上を向くジオメトリで使用される標準座標系を使用します。 Direct2D では、正の y 軸が下向きの Windows 座標系を使用します。
x 軸と線 (0,0) から P' の間の角度は Φ + Θ です。 次の ID が保持されます。
- x = R cosΦ y = R sinΦ x' = R cos(Φ + Θ) y' = R sin(Φ+ Θ)
次に、Θ の観点から x' と y' を解決します。 三角関数の加算式:
- x' = R(cosΦcosΘ – sinΦsinΘ) = RcosΦcosΘ – RsinΦsinΘ y' = R(sinΦcosΘ + cosΦsinΘ) = RsinΦcosΘ + RcosΦsinΘ
代わりに、次の処理が行われます。
- x' = xcosΘ – ysinΘ y' = xsinΘ + ycosΘ
これは、前に示した変換されたポイント P' に対応します。
任意の点の周りの回転
原点以外の点(x,y)を中心に回転するには、次の行列が使用されます。
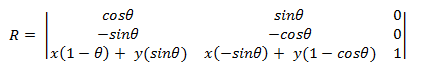
ポイント (x,y) を原点とすることで、この行列を派生させることができます。
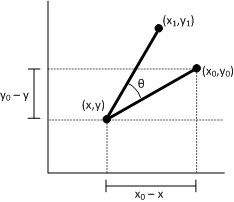
(x1, y1) は、点 (x0, y0) を点 (x,y) の周りに回転させた結果の点とします。 次のように x1 を派生させることができます。
- x1 = (x0 – x)cosΘ– (y0 – y)sinΘ + x x1 = x0cosΘ – y0sinΘ + \[ (1 – cosΘ) + ysinΘ \]
次に、前の数式 x1 = ax0 + cy0 + e を使用して、この数式を変換行列に戻します。 y1 を派生するには、同じ手順を使用します。
スキュー変換
スキュー変換は、次の 4 つのパラメーターによって定義されます。
- Θ: x 軸に沿って傾斜する量を、y 軸からの角度として測定します。
- Φ: y 軸に沿って傾斜する量を x 軸からの角度として測定します。
- (px, py): スキューが実行される点の x 座標と y 座標。
スキュー変換では、次の行列が使用されます。
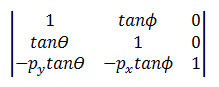
変換されたポイントは次のとおりです。
- P' = (*x* + *y*tanΘ – *py*tanΘ, *y* + *x*tanΦ) – *py*tanΦ
または同等:
- P' = (*x* + (*y* – *py*)tanΘ, *y* + (*x* – *px*)tanΦ)
この変換のしくみを確認するには、各コンポーネントを個別に検討してください。 Θ パラメータは、x 方向のすべての点を tanΘ と等しい量だけ移動します。 次の図は、Θ と x 軸スキューの関係を示しています。
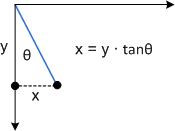
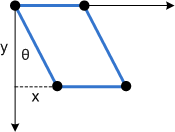
四角形に適用されるのと同じ傾斜を次に示します。
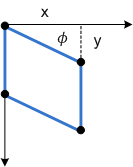
Φパラメータは同じ効果を持ちますが、y軸に沿って:
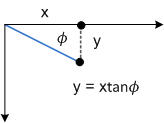
次の図は、四角形に適用される y 軸の傾斜を示しています。
最後に、パラメーター px と py は 、x 軸と y 軸に沿ってスキューの中心点をシフトします。
Direct2D での変換の表し方
Direct2D 変換はすべてアフィン変換です。 Direct2D では、非アフィン変換はサポートされていません。 変換は、 D2D1_MATRIX_3X2_F 構造体によって表されます。 この構造体は、3 × 2 行列を定義します。 アフィン変換の 3 番目の列は常に同じ ([0, 0, 1])、Direct2D は非アフィン変換をサポートしていないため、3 × 3 行列全体を指定する必要はありません。 内部的には、Direct2D は 3 × 3 つのマトリックスを使用して変換を計算します。
D2D1_MATRIX_3X2_Fのメンバーは、インデックス位置に従って名前が付けられます。_11 メンバーは要素 (1,1)、_12 メンバーは要素 (1,2) などです。 構造体メンバーは直接初期化できますが、 D2D1::Matrix3x2F クラスを使用することをお勧めします。 このクラスは D2D1_MATRIX_3X2_F を継承し、基本的なアフィン変換を作成するためのヘルパー メソッドを提供します。 クラスでは、Direct2D での変換の適用に関するページで説明されているように、2 つ以上の変換を作成するための operator*() も定義します。
次へ