Guia para a linguagem de especificação de rede neural Net# para o Machine Learning Studio (clássico)

APLICA-SE A: Machine Learning Studio (clássico) Azure Machine Learning

Net# é uma linguagem desenvolvida pela Microsoft usada para definir arquiteturas de redes neurais complexas, como redes neurais profundas ou convoluções de dimensões arbitrárias. Você pode usar as estruturas complexas para aprimorar o aprendizado sobre dados, como áudio, vídeo ou imagem.

Você pode usar uma especificação de arquitetura Net# em todos os módulos de rede neural no Machine Learning Studio (clássico):

• Rede Neural Multiclasse
• Rede Neural de Duas Classes
• Regressão de Rede Neural

Este artigo descreve os conceitos básicos e a sintaxe necessária para desenvolver uma rede neural personalizada usando Net#:

• Requisitos da rede neural e como definir os componentes primários
• A sintaxe e palavras-chave da linguagem de especificação Net#
• Exemplos de redes neurais personalizadas criadas usando Net#

Conceitos básicos de rede neural

Uma estrutura de rede neural composta por nós que são organizados em camadas e conexões ponderadas (ou bordas) entre os nós. As conexões são direcionais e cada conexão tem um nó de origem e um nó de destino.

Cada camada treinável (uma camada oculta ou de saída) tem um ou mais pacotes de conexão. Um grupo de conexões consiste de uma camada de origem e uma especificação das conexões dessa camada de origem. Todas as conexões em determinado pacote compartilham camadas de origem e destino. Em Net#, um grupo de conexões é considerado como pertencente à camada de destino do grupo.

A Net# é compatível com vários tipos de conjuntos de conexão, o que permite personalizar o modo como as entradas são mapeadas para camadas ocultas e para saídas.

O grupo padrão ou standard é um grupo completo, no qual cada nó na camada de origem é conectado a todos os nós na camada de destino.

Adicionalmente, a Net# dá suporte aos quatro tipos de grupos de conexão avançados a seguir:

• Grupos filtrados. Você pode definir um predicado utilizando os locais do nó de camada de origem e de destino. Os nós são conectados sempre que o predicado é Verdadeiro.

• Grupos convolucionais. Você pode definir pequenas zonas próximas de nós na camada de origem. Cada nó na camada de destino está conectado a uma zona próxima de nós na camada de origem.

• Grupos de pooling e Grupos de normalização de resposta. Estes são similares a grupos convolucionais, no sentido que o usuário define pequenas zonas próximas de nós na camada de origem. A diferença é que a ponderação das bordas nesses grupos não são treináveis. Em vez disso, uma função predefinida é aplicada aos valores de nó de origem para determinar o valor do nó de destino.

Personalizações com suporte

A arquitetura dos modelos de rede neural que você cria no Machine Learning Studio (clássico) pode ser amplamente personalizada usando Net#. Você poderá:

• Criar camadas ocultas e controlar o número de nós em cada camada.
• Especifique como as camadas devem conectar-se umas às outras.
• Definir estruturas de conectividade especial, como convoluções e grupos de compartilhamento de peso.
• Especifique diferentes funções de ativação.

Para obter detalhes sobre a sintaxe da linguagem de especificação, veja Especificação de Estrutura.

Para ver exemplos de como definir redes neurais para algumas tarefas comuns de aprendizado de máquina, das simples às complexas, veja Exemplos.

Requisitos gerais

• É preciso que haja exatamente uma camada de saída, pelo menos uma camada de entrada e nenhuma ou mais camadas ocultas.
• Cada camada tem um número fixo de nós, arranjados conceitualmente em uma matriz retangular de dimensões arbitrárias.
• As camadas de entrada não têm parâmetros treinados associados e representam o ponto no qual os dados da instância entram na rede.
• As camadas treináveis (as camadas ocultas e de saída) têm parâmetros treinados associados, conhecidos como pesos e vieses.
• Os nós de origem e destino precisam estar em camadas separadas.
• As conexões precisam ser acíclicas; em outras palavras, não pode haver uma cadeia de conexões levando de volta ao nó de origem inicial.
• A camada de saída não pode ser uma camada de origem de um grupo de conexões.

Especificações de estrutura

Uma especificação de estrutura de rede neural é composta por três seções: a declaração de constante, a declaração de camada e a declaração de conexão. Há também uma seção declaração de compartilhamento opcional. As seções podem ser especificadas em qualquer ordem.

Declaração de constante

Uma declaração de constante é opcional. Ela fornece um meio para definir valores usados em outro lugar na definição de rede neural. Uma instrução de declaração consiste de um identificador seguido por um sinal de igual e uma expressão de valor.

Por exemplo, a instrução a seguir define uma constante x:

Const X = 28;

Para definir duas ou mais constantes simultaneamente, coloque os nomes de identificador e os valores entre chaves e separe-os usando ponto e vírgula. Por exemplo:

Const { X = 28; Y = 4; }

O lado direito de cada expressão de atribuição pode ser um número inteiro, um número real, um valor booliano (verdadeiro ou falso) ou uma expressão matemática. Por exemplo:

Const { X = 17 * 2; Y = true; }

Declaração de camada

A declaração de camada é obrigatória. Ela define o tamanho e a origem da camada, incluindo seus pacotes de conexão e atributos. A instrução de declaração começa pelo nome da camada (entrada, oculta ou saída), seguida pelas dimensões da camada (uma tupla de números inteiros positivos). Por exemplo:

input Data auto;
hidden Hidden[5,20] from Data all;
output Result[2] from Hidden all;

• O produto das dimensões é o número de nós na camada. Neste exemplo, há duas dimensões [5, 20], o que significa que há 100 nós na camada.
• As camadas podem ser declaradas em qualquer ordem, com uma exceção: se mais do que uma camada de entrada for definida, a ordem em que elas são declaradas precisa corresponder à ordem dos recursos nos dados de entrada.

Para especificar que o número de nós em uma camada seja determinado automaticamente, use a palavra-chave auto. A palavra-chave auto tem efeitos diferentes, dependendo da camada:

• Em uma declaração de camada de entrada, o número de nós é o número de recursos nos dados de entrada.
• Em uma declaração de camada oculta, o número de nós é o número especificado pelo valor do parâmetro para Número de nós ocultos.
• Em uma declaração de camada de saída, o número de nós é 2 para classificação em duas categorias, 1 para regressão e igual ao número de nós de saída para classificação multiclasse.

Por exemplo, a definição de rede a seguir permite que o tamanho de todas as camadas seja determinado automaticamente:

input Data auto;
hidden Hidden auto from Data all;
output Result auto from Hidden all;

Uma declaração de camada para uma camada que pode ser treinada (as camadas ocultas ou de saída) pode incluir, opcionalmente, a função de saída (também chamada de função de ativação), que utiliza como valor padrão sigmoid para modelos de classificação e linear para modelos de regressão. Mesmo que você use o padrão, é possível declarar explicitamente a função de ativação, se desejado para esclarecimento.

Há suporte para as funções de saída a seguir:

• sigmoid
• linear
• softmax
• rlinear
• square
• sqrt
• srlinear
• abs
• tanh
• brlinear

Por exemplo, a declaração a seguir usa a função softmax:

output Result [100] softmax from Hidden all;

Declaração de conexão

Imediatamente após definir a camada treinável, você precisa declarar conexões entre as camadas que definiu. A declaração do grupo de conexões começa pela palavra-chave from, seguida do nome da camada de origem do grupo e do tipo de grupo de conexões a criar.

Atualmente, há suporte para cinco tipos de grupos de conexão:

• Grupos completos, indicados pela palavra-chave all
• Grupos filtrados, indicados pela palavra-chave where, seguida por uma expressão predicada
• Grupos convolucionais, indicados pela palavra-chave convolve, seguida pelos atributos de convolução
• Grupos de pooling, indicados pelas palavras-chaves max pool ou mean pool
• Grupos de normalização de resposta, indicados pela palavra-chave response norm

Grupos completos

Um grupo de conexões completo inclui uma conexão de cada nó na camada de origem para cada nó na camada de destino. Esse é o tipo de conexão de rede padrão.

Grupos filtrados

Uma especificação grupo de conexões filtrado inclui um predicado, expresso sintaticamente de modo muito similar a uma expressão lambda em C#. O exemplo a seguir define dois grupos filtrados:

input Pixels [10, 20];
hidden ByRow[10, 12] from Pixels where (s,d) => s[0] == d[0];
hidden ByCol[5, 20] from Pixels where (s,d) => abs(s[1] - d[1]) <= 1;

• No predicado de ByRow, s é um parâmetro representando um índice na matriz retangular de nós da camada de entrada Pixels e d é um parâmetro representando um índice na matriz de nós da camada oculta ByRow. O tipo de s e d é uma tupla de dois números inteiros. Conceitualmente, s abrange todos os pares de números inteiros com 0 <= s[0] < 10 e 0 <= s[1] < 20 enquanto d abrange todos os pares de números inteiros com 0 <= d[0] < 10 e 0 <= d[1] < 12.

• No lado direito da expressão predicada, há uma condição. Neste exemplo, para cada valor de s e d de modo que a condição seja Verdadeira, há um limite por meio do nó da camada de origem para o nó da camada de destino. Assim, essa expressão de filtragem indica que o grupo inclui uma conexão por meio do nó definido por s para o nó definido por d, em todos os casos em que s[0] for igual a d[0].

Opcionalmente, você pode especificar um conjunto de pesos para um grupo filtrado. O valor para o atributo Weights deve ser uma tupla de valores de pontos flutuantes com um comprimento correspondente ao número de conexões definidas pelo pacote. Por padrão, os pesos são gerados de modo aleatório.

Valores de peso são agrupados pelo índice do nó de destino. Ou seja, se o primeiro nó de destino está conectado a K nós de origem, os primeiros K elementos da tupla Weights são os pesos para o primeiro nó de destino, na ordem do índice de origem. O mesmo se aplica aos nós de destino restantes.

É possível especificar pesos diretamente como valores constantes. Por exemplo, se você souber os pesos anteriormente, pode especificá-los como constantes usando esta sintaxe:

const Weights_1 = [0.0188045055, 0.130500451, ...]

Grupos convolucionais

Quando os dados de treinamento têm uma estrutura homogênea, conexões convolucionais são usadas para aprender os recursos de alto nível dos dados. Por exemplo, para dados de imagem, áudio ou vídeo, a dimensionalidade espacial ou temporal pode ser bastante uniforme.

Grupos convolucionais utilizam kernels retangulares, que deslizam entre as dimensões. Essencialmente, cada kernel define um conjunto de pesos aplicados em zonas próximas locais, ao qual nos referimos como aplicativos de kernel. Cada aplicativo de kernel corresponde a um nó na camada de origem, que é conhecido como o nó central. Os pesos de um kernel são compartilhados entre muitas conexões. Em um grupo convolucional, cada kernel é retangular e todos os aplicativos de kernel têm o mesmo tamanho.

Grupos convolucionais dão suporte aos seguintes atributos:

InputShape define a dimensionalidade da camada de origem para as finalidades deste grupo convolucional. O valor precisa ser uma tupla de números inteiros positivos. O produto dos inteiros precisa ser igual ao número de nós na camada de origem, mas com exceção disso, não precisam corresponder à dimensionalidade declarada para a camada de origem. O tamanho dessa tupla torna-se o valor de aridade para o grupo convencional. Tipicamente, refere-se ao número de argumentos ou operandos que uma função pode utilizar.

Para definir a forma e os locais dos kernels, use os atributos KernelShape, Stride, Padding, LowerPad e UpperPad:

• KernelShape: (obrigatório) define a dimensionalidade de cada kernel para o grupo convolucional. O valor deve ser uma tupla de inteiros positivos com um comprimento igual à aridade do pacote. Cada componente dessa tupla não pode ser maior que o componente correspondente de InputShape.

• Stride: (opcional) define o tamanho de etapas deslizantes de convolução (um tamanho de etapa para cada dimensão), que é a distância entre os nós centrais. O valor deve ser uma tupla de inteiros positivos com um comprimento igual à aridade do grupo. Cada componente dessa tupla não pode ser maior que o componente correspondente de KernelShape. O valor padrão é uma tupla com todos os componentes iguais a um.

• Sharing: (opcional) define o compartilhamento de peso para cada dimensão da convolução. O valor pode ser um único valor booliano ou uma tupla de valores booleanos com um comprimento igual à aridade do pacote. Um único valor Booliano é estendido para ser uma tupla do tamanho correto, com todos os componentes iguais ao valor especificado. O valor padrão é uma tupla composta por todos os valores Verdadeiros.

• MapCount: (opcional) define o número de mapas de recurso para o grupo convolucional. O valor pode ser um único inteiro positivo ou uma tupla de inteiros positivos com um comprimento igual à aridade do pacote. Um único número inteiro positivo é estendido para ser uma tupla do tamanho correto, com os primeiros componentes iguais ao valor especificado e todos os componentes restantes iguais a um. O valor padrão é um. O número total de mapas de recurso é o produto dos componentes da tupla. O cálculo da alíquota desse número total pelos componentes determina como os valores do mapa de recursos são agrupados nos nós de destino.

• Weights: (opcional) define os pesos iniciais para o grupo. O valor deve ser uma tupla de valores de pontos flutuantes com um comprimento igual ao número de kernels vezes o número de pesos por kernel, conforme definido neste artigo. Os pesos padrão são gerados aleatoriamente.

Há dois conjuntos de propriedades que controlam o preenchimento, sendo as propriedades mutuamente exclusivas:

• Padding: (opcional) determina se a entrada deve ser preenchida usando um esquema de preenchimento padrão. O valor pode ser um único valor booliano ou uma tupla de valores boolianos com comprimento igual à aridade do pacote.

  Um único valor Booliano é estendido para ser uma tupla do tamanho correto, com todos os componentes iguais ao valor especificado.

  Se o valor para uma dimensão é Verdadeiro, a origem é preenchida logicamente naquela dimensão com células de valor zero, para dar suporte aplicativos de kernel adicionais de modo que os nós centrais do primeiro e último kernels naquela dimensão sejam o primeiro e último nós naquela dimensão, na camada de origem. Assim, o número de nós "falsos" em cada dimensão é determinado automaticamente, de modo a ajustar exatamente (InputShape[d] - 1) / Stride[d] + 1 kernels na camada preenchida de origem.

  Se o valor para uma dimensão é falso, os kernels são definidos de modo que o número de nós deixados de fora em cada lado é o mesmo (podendo chegar até uma diferença de 1). O valor padrão desse atributo é uma tupla com todos os componentes iguais a Falso.

• UpperPad e LowerPad: (opcional) fornecem maior controle sobre a quantidade de preenchimento a ser usada. Importante: esses atributos podem ser definidos se e somente se a propriedade Preenchimento acima não estiver definida. Os valores devem ser tuplas de números inteiros com comprimentos igual à aridade do pacote. Quando esses atributos são especificados, nós "falsos" são adicionados às extremidades inferior e superior de cada dimensão da camada de entrada. O número de nós adicionados às extremidades inferior e superior em cada dimensão é determinado por LowerPad[i] e UpperPad[i], respectivamente.

  Para assegurar que os kernels correspondam somente a nós "reais" e não a nós "falsos", as condições a seguir precisam ser satisfeitas:

  • Cada componente de LowerPad precisa ser estritamente menor que KernelShape[d]/2.

  • Cada componente de UpperPad não pode ser maior que KernelShape[d]/2.

  • O valor padrão desses atributos é uma tupla com todos os componentes iguais a 0.

    A configuração Padding = true permite o preenchimento necessário para manter o "centro" do kernel dentro da entrada "real". Isso altera um pouco o cálculo para computar o tamanho da saída. Em geral, o tamanho da saída D é computado como D = (I - K) / S + 1, em que I é o tamanho da entrada, K é o tamanho do kernel, S é o stride e / é a divisão do número inteiro (aproximado para zero). Se você definir UpperPad = [1, 1], o tamanho da entrada I será efetivamente 29 e, portanto, D = (29 - 5) / 2 + 1 = 13. No entanto, quando Padding = true, essencialmente I e aumentado por K - 1; com isso, D = ((28 + 4) - 5) / 2 + 1 = 27 / 2 + 1 = 13 + 1 = 14. Ao especificar os valores para UpperPad e LowerPad, você obtém muito mais controle sobre o preenchimento do que se configurar apenas Padding = true.

Para mais informações sobre redes convolucionais e seus aplicativos, consulte esses artigos:

• http://d2l.ai/chapter_convolutional-neural-networks/lenet.html
• https://research.microsoft.com/pubs/68920/icdar03.pdf

Grupos de pooling

Um grupo de pooling aplica geometria similar à da conectividade convolucional, mas usa funções predefinidas para gerar valores de nó de origem a fim de derivar o valor do nó de destino. Assim, os grupos de pooling não têm estado treinável (pesos ou vieses). Grupos de pooling dão suporte a todos os atributos convolucionais, exceto Sharing, MapCount e Weights.

Tipicamente, os kernels resumidos pelas unidades de pooling adjacentes não se sobrepõem. Se Stride[d] é igual a KernelShape[d] em cada dimensão, a camada obtida é a tradicional camada de pooling local, utilizada frequentemente em redes neurais convolucionais. Cada nó de destino computa o valor máximo ou então a média das atividades de seu kernel na camada de origem.

O exemplo a seguir ilustra um grupo de pooling:

hidden P1 [5, 12, 12]
  from C1 max pool {
  InputShape  = [ 5, 24, 24];
   KernelShape = [ 1,  2,  2];
   Stride      = [ 1,  2,  2];
  }

• O arity do pacote é 3: ou seja, o comprimento das tuplas InputShape, KernelShape, e Stride.
• O número de nós na camada de origem é 5 * 24 * 24 = 2880.
• Essa é uma camada de pooling local tradicional porque KernelShape e Stride são iguais.
• O número de nós na camada de destino é 5 * 12 * 12 = 1440.

Para mais informações sobre camadas de pooling, consulte esses artigos:

• https://www.cs.toronto.edu/~hinton/absps/imagenet.pdf (Seção 3.4)
• https://cs.nyu.edu/~koray/publis/lecun-iscas-10.pdf
• https://cs.nyu.edu/~koray/publis/jarrett-iccv-09.pdf

Grupos de normalização de resposta

A normalização de resposta é um esquema de normalização local introduzido por Geoffrey Hinton, com outros autores, no artigo ImageNet Classification with Deep Convolutional Neural Networks (Classificação ImageNet com redes neurais convolucionais profundas).

A normalização de resposta é usada para auxiliar na generalização de redes neurais. Quando um neurônio está disparando em um nível de ativação muito alto, uma camada de normalização de resposta local suprime o nível de ativação dos neurônios circundantes. Isso é feito usando três parâmetros (α, β e k) e uma estrutura convolucional (ou forma de zona próxima). Todo neurônio na camada de destino y corresponde a um neurônio x na camada de origem. O nível de ativação de y é fornecido pela fórmula a seguir, na qual f é o nível de ativação de um neurônio, e Nx é o kernel (ou o conjunto contendo os neurônios na zona próxima a x), conforme definido pela seguinte estrutura convolucional:

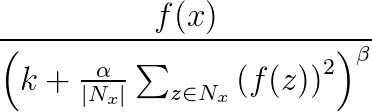
Os grupos de normalização de resposta dão suporte a todos os atributos convolucionais, exceto Sharing, MapCount e Weights.

• Se o kernel contém neurônios no mesmo mapa que x, nos referimos ao esquema de normalização como normalização do mesmo mapa. Para definir a normalização de mesmo mapa, a primeira coordenada em InputShape precisa ter o valor 1.

• Se o kernel contém neurônios na mesma posição espacial que x, mas os neurônios estão em outros mapas, o esquema de normalização é chamado de normalização entre mapas. Esse tipo de normalização de resposta implementa um tipo de inibição lateral inspirada no tipo encontrado em neurônios reais, criando concorrência por níveis elevados de ativação entre as saídas de neurônio computadas em mapas diferentes. Para definir a normalização entre mapas, a primeira coordenada precisa ser um número inteiro maior que um e que não seja maior que o número de mapas, enquanto o resto das coordenadas deve ter o valor 1.

Já que os grupos de normalização de resposta aplicam uma função predefinida aos valores de nó de origem para determinar o valor do nó de destino, eles não têm estado treinável (pesos ou vieses).

Além dos quatro atributos descritos anteriormente, grupos de normalização de resposta também dão suporte aos seguintes atributos:

• Alpha: (obrigatório) especifica um valor de ponto flutuante que corresponde a α na fórmula anterior.
• Beta: (obrigatório) especifica um valor de ponto flutuante que corresponde a β na fórmula anterior.
• Offset: (opcional) especifica um valor de ponto flutuante que corresponde a k na fórmula anterior. Seu valor padrão é 1.

O exemplo a seguir define um grupo de normalização de resposta usando esses atributos:

hidden RN1 [5, 10, 10]
from P1 response norm {
  InputShape  = [ 5, 12, 12];
  KernelShape = [ 1,  3,  3];
  Alpha = 0.001;
  Beta = 0.75;
  }

• A camada de origem inclui cinco mapas, cada um com dimensão de 12 x 12, totalizando 1.440 nós.
• O valor de KernelShape indica que esta é uma camada de normalização de mesmo mapa, no qual a zona próxima é uma retângulo de 3x3.
• O valor padrão de Padding é Falso, portanto, a camada tem apenas 10 nós em cada dimensão. Para incluir um nó na camada de destino correspondente a cada nó da camada de origem, adicione Padding = [true, true, true]; então, altere o tamanho de RN1 para [5, 12, 12].

Declaração de compartilhamento

Net# dá suporte, opcionalmente, a definição de múltiplos grupos com pesos compartilhados. Os pesos de quaisquer dois grupos pode ser compartilhado se suas estruturas forem iguais. A sintaxe a seguir define grupos com pesos compartilhados:

share-declaration:
  share    {    layer-list    }
  share    {    bundle-list    }
  share    {    bias-list    }

  layer-list:
    layer-name    ,    layer-name
    layer-list    ,    layer-name

  bundle-list:
    bundle-spec    ,    bundle-spec
    bundle-list    ,    bundle-spec

  bundle-spec:
    layer-name    =>     layer-name

  bias-list:
    bias-spec    ,    bias-spec
    bias-list    ,    bias-spec

  bias-spec:
    1    =>    layer-name

  layer-name:
    identifier

Por exemplo, a declaração de compartilhamento a seguir especifica os nomes de camada, indicando que tanto pesos quanto vieses devem ser compartilhados:

Const {
  InputSize = 37;
  HiddenSize = 50;
  }
input {
  Data1 [InputSize];
  Data2 [InputSize];
  }
hidden {
  H1 [HiddenSize] from Data1 all;
  H2 [HiddenSize] from Data2 all;
  }
output Result [2] {
  from H1 all;
  from H2 all;
  }
share { H1, H2 } // share both weights and biases

• Os recursos de entrada são particionados em duas camadas de entrada de mesmo tamanho.
• As camadas ocultas, então, computam recursos de nível elevado nas duas camadas de entradas.
• A declaração de compartilhamento especifica que H1 e H2 precisam ser computados do mesmo modo que suas respectivas entradas.

Alternativamente, isso pode ser especificado com duas declarações de compartilhamento separadas, como descrito a seguir:

share { Data1 => H1, Data2 => H2 } // share weights
<!-- -->
    share { 1 => H1, 1 => H2 } // share biases

Você pode usar a forma abreviada somente quando as camadas contiverem um único grupo. Em geral, é possível compartilhar somente quando a estrutura relevante é idêntica, significando que elas têm o mesmo tamanho, mesma geometria convolucional e assim por diante.

Exemplos de uso do Net#

Esta seção oferece alguns exemplos de como você pode usar o Net# para acrescentar camadas ocultas, definir o modo pelo qual as camadas ocultas interagem com outras camadas e compilar redes convolucionais.

Defina uma rede neural personalizada simples: exemplo "Olá mundo"

Este exemplo simples demonstra como criar um modelo de rede neural que tem uma única camada oculta.

input Data auto;
hidden H [200] from Data all;
output Out [10] sigmoid from H all;

O exemplo ilustra alguns comandos básicos da seguinte maneira:

• A primeira linha define a camada de entrada (denominada Data). Quando você usa a palavra-chave auto, a rede neural automaticamente inclui todas as colunas de recurso nos exemplos de entrada.
• A segunda linha cria a camada oculta. O nome H é atribuído à camada oculta, que tem 200 nós. Essa camada é totalmente conectada à camada de entrada.
• A terceira linha define a camada de saída (denominada Out), que contém 10 nós de saída. Se a rede neural for usada para classificação, haverá um nó de saída por classe. A palavra-chave sigmoide indica que a função de saída é aplicada à camada de saída.

Definir várias camadas ocultas: exemplo de visão do computador

O exemplo a seguir demonstra como definir uma rede neural um pouco mais complexa, com múltiplas camadas ocultas personalizadas.

// Define the input layers
input Pixels [10, 20];
input MetaData [7];

// Define the first two hidden layers, using data only from the Pixels input
hidden ByRow [10, 12] from Pixels where (s,d) => s[0] == d[0];
hidden ByCol [5, 20] from Pixels where (s,d) => abs(s[1] - d[1]) <= 1;

// Define the third hidden layer, which uses as source the hidden layers ByRow and ByCol
hidden Gather [100]
{
from ByRow all;
from ByCol all;
}

// Define the output layer and its sources
output Result [10]
{
from Gather all;
from MetaData all;
}

Este exemplo ilustra vários recursos da linguagem de especificação de redes neurais:

• A estrutura conta com duas camadas de entrada, Pixels e MetaData.
• A camada Pixels é uma camada de origem para dois grupos de conexões, com as camadas de destino ByRow e ByCol.
• As camadas Gather e Result são camadas de destino em múltiplos grupos de conexões.
• A camada de saída, Result, é uma camada de destino em dois grupos de conexões; um com a camada oculta de segundo nível Gather como uma camada de destino e o outro com a camada de entrada MetaData como uma camada de destino.
• As camadas ocultas, ByRow e ByCol, especificam conectividade filtrada usando expressões de predicado. Mais precisamente, o nó em ByRow [x, y] está conectado aos nós em Pixels, que têm a primeira coordenada de índice igual à primeira coordenada do nó, x. Da mesma forma, o nó em ByCol em [x, y] está conectado aos nós em Pixels, que têm a segunda coordenada de índice dentro da segunda coordenada do nó, y.

Definir uma rede convolucional para classificação multiclasse: exemplo de reconhecimento de dígitos

A definição de rede a seguir foi projetada para reconhecer números e ilustra algumas técnicas avançadas para personalizar uma rede neural.

input Image [29, 29];
hidden Conv1 [5, 13, 13] from Image convolve
  {
  InputShape  = [29, 29];
  KernelShape = [ 5,  5];
  Stride      = [ 2,  2];
  MapCount    = 5;
  }
hidden Conv2 [50, 5, 5]
from Conv1 convolve
  {
  InputShape  = [ 5, 13, 13];
  KernelShape = [ 1,  5,  5];
  Stride      = [ 1,  2,  2];
  Sharing     = [false, true, true];
  MapCount    = 10;
  }
hidden Hid3 [100] from Conv2 all;
output Digit [10] from Hid3 all;

• A estrutura tem uma única camada de entrada, Image.

• A palavra-chave convolve indica que as camadas denominadas Conv1 e Conv2 são camadas convolucionais. Cada uma dessas declarações de camada é seguida de uma lista dos atributos de convolução.

• A rede tem uma terceira camada oculta, Hid3, que é totalmente conectada à Conv2, a segunda camada oculta.

• A camada de saída, Digit, é conectada somente à terceira camada oculta, Hid3. A palavra-chave all indica que a camada de saída está totalmente conectada a Hid3.

• A arity da convolução é três: o tamanho das tuplas InputShape, KernelShape, Stride e Sharing.

• O número de pesos por kernel é 1 + KernelShape\[0] * KernelShape\[1] * KernelShape\[2] = 1 + 1 * 5 * 5 = 26. Ou 26 * 50 = 1300.

• Você pode calcular os nós em cada camada oculta, conforme descrito a seguir:

  NodeCount\[0] = (5 - 1) / 1 + 1 = 5 NodeCount\[1] = (13 - 5) / 2 + 1 = 5 NodeCount\[2] = (13 - 5) / 2 + 1 = 5

• O número total de nós pode ser calculado usando a dimensionalidade declarada da camada, [50, 5, 5], conforme descrito a seguir: MapCount * NodeCount\[0] * NodeCount\[1] * NodeCount\[2] = 10 * 5 * 5 * 5

• Como Sharing[d] é False apenas para d == 0, o número de kernels é MapCount * NodeCount\[0] = 10 * 5 = 50.

Agradecimentos

A linguagem Net# para personalizar a arquitetura das redes neurais foi desenvolvida na Microsoft por Shon Katzenberger (arquiteto, Machine Learning) e Alexey Kamenev (engenheiro de software, Microsoft Research). Ela é usada internamente para projetos de aprendizado de máquina e aplicativos que vão de detecção de imagem a análise de texto. Para saber mais, confira Redes neurais no Machine Learning Studio – Introdução ao Net#