Transformação da projeção
Uma transformação de projeção controla os componentes internos da câmera, como escolher uma lente para uma câmera. Este é o mais complicado dos três tipos de transformação.
A matriz de projeção é tipicamente uma projeção de escala e perspectiva. A transformação de projeção converte o tronco de visualização em uma forma cuboide. Como a extremidade próxima do tronco de visualização é menor que a extremidade oposta, isso tem o efeito de expandir os objetos que estão próximos à câmera; É assim que a perspectiva é aplicada à cena.
No tronco de exibição, a distância entre a câmera e a origem do espaço de transformação de exibição é definida arbitrariamente como D, de modo que a matriz de projeção se parece com a ilustração a seguir.
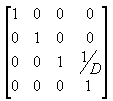
A matriz de visualização traduz a câmera para a origem traduzindo na direção z por - D. A matriz de tradução é como a ilustração a seguir.
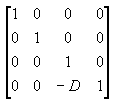
Multiplicando a matriz de translação pela matriz de projeção (T*P) obtém-se a matriz de projeção composta, conforme mostrado na ilustração a seguir.
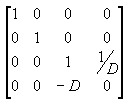
A transformação de perspectiva converte um tronco de visualização em um novo espaço de coordenadas. Observe que o tronco se torna paralelepípedo e também que a origem se move do canto superior direito da cena para o centro, conforme mostrado no diagrama a seguir.
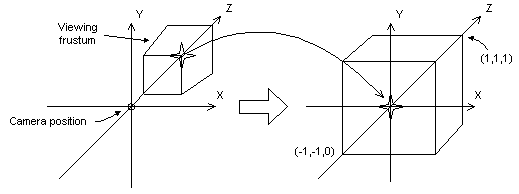
Na transformada de perspectiva, os limites das direções x e y são -1 e 1. Os limites da direção z são 0 para o plano frontal e 1 para o plano traseiro.
Essa matriz converte e dimensiona objetos com base em uma distância especificada da câmera até o plano de recorte próximo, mas não considera o campo de visão (fov), e os valores z que ela produz para objetos à distância podem ser quase idênticos, dificultando as comparações de profundidade. A matriz a seguir aborda esses problemas e ajusta os vértices para levar em conta a taxa de proporção da janela de visualização, tornando-a uma boa opção para a projeção de perspectiva.
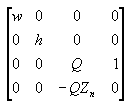
Nesta matriz, Zn é o valor z do plano de recorte próximo. As variáveis w, h e Q têm os seguintes significados. Observe que fovw e fovk representam os campos de visão horizontal e vertical da janela de visualização, em radianos.
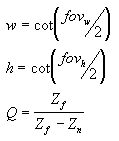
Para seu aplicativo, usar ângulos de campo de visão para definir os coeficientes de escala x e y pode não ser tão conveniente quanto usar as dimensões horizontais e verticais da janela de exibição (no espaço da câmera). À medida que a matemática funciona, as duas equações a seguir para w e h usam as dimensões da janela de visualização e são equivalentes às equações anteriores.
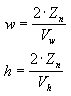
Nessas fórmulas, Zn representa a posição do plano de recorte próximo, e as variáveis Vw e Vh representam a largura e a altura da janela de visualização, no espaço da câmera.
Seja qual for a fórmula que você decidir usar, certifique-se de definir Zn para o maior valor possível, porque os valores z extremamente próximos da câmera não variam muito. Isso torna as comparações de profundidade usando z-buffers de 16 bits um tanto complicadas.
Uma matriz de projeção compatível com w
O Direct3D pode usar o componente w de um vértice que foi transformado pelas matrizes de mundo, exibição e projeção para executar cálculos baseados em profundidade em efeitos de buffer de profundidade ou neblina. Cálculos como esses exigem que sua matriz de projeção normalize w para ser equivalente ao espaço-mundo z. Resumindo, se sua matriz de projeção incluir um coeficiente (3,4) que não seja 1, você deve dimensionar todos os coeficientes pelo inverso do coeficiente (3,4) para fazer uma matriz adequada. Se você não fornecer uma matriz compatível, os efeitos de neblina e o buffer de profundidade não serão aplicados corretamente.
A ilustração a seguir mostra uma matriz de projeção não compatível e a mesma matriz dimensionada para que a névoa relativa aos olhos seja habilitada.

Nas matrizes anteriores, todas as variáveis são consideradas diferentes de zero. Para obter informações sobre buffer de profundidade baseado em w, consulte Buffers de profundidade.
O Direct3D usa a matriz de projeção definida atualmente em seus cálculos de profundidade baseados em w. Como resultado, os aplicativos devem definir uma matriz de projeção compatível para receber os recursos baseados em w desejados, mesmo que não usem o Direct3D para transformações.
Tópicos relacionados