Curvas de parâmetro

  • Artigo

Os parâmetros de mídia são capazes de seguir uma curva ao longo do tempo. Cada curva é descrita por uma fórmula matemática e dois pontos de extremidade. Cada ponto de extremidade é definido por um tempo de referência e o valor da curva nesse momento. A fórmula é usada para calcular valores intermediários entre os pontos e determina a forma da curva. As curvas possíveis são:

  • Saltar
  • Linear
  • Square
  • Quadrado inverso
  • Seno

"Jump" significa ir diretamente para o valor final. As outras curvas são mostradas no diagrama a seguir.

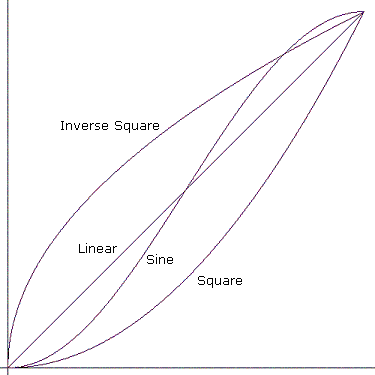
curvas de parâmetro

Matematicamente, as curvas funcionam da seguinte maneira. Suponha que uma curva comece no momento t₀ com um valor de v₀ e termine no momento t₁ com um valor de v₁. Os dois pontos que definem a curva são (t₀, v₀) e (t₁, v₁).

  • Deixe que Δnão seja a duração total da curva, t₁-t₀.
  • Let Δv be the interval between the starting and ending values, v₁-v₀.
  • A qualquer momento t tal que t₀ <= t<= t₁, let Δt' = t-t₀.

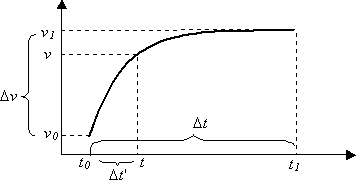
cálculo de parâmetro

O valor do parâmetro no momento t é:

v = f( Δt' / Δt ) * Δv v + ₀

em que f(x) é uma função determinada pelo tipo de curva:

  • Linear: y = x
  • Quadrado: y = x^2
  • Quadrado inverso: y = sqrt(x)
  • Seno: y = [ sin(πx – π/2) + 1 ] / 2

Observe que Δt' < Δt, portanto, o termo Δt'/Δt varia de 0 a 1. Portanto, f(x) também varia de 0 a 1 e v sempre fica entre v₀ e v₁. Isso é verdadeiro se v₀ <v₁ ou vice-versa. Em outras palavras, a curva é limitada pelo retângulo (t₀, v₀, t₁, v₁).

Para a curva de seno, o valor de (πx – π/2) varia de –π/2 a π/2, o que significa que sin(πx – π/2) varia de –1 a 1. Em seguida, o resultado é normalizado para que f(x) caia no intervalo (0-1).

Parâmetros de mídia