T-portarnas och T-fabrikernas roll i kvantberäkning
I den här artikeln beskrivs T-portarnas och T-fabrikernas roll i feltolerant kvantberäkning. Genom att ge en kvantalgoritm blir uppskattningen av nödvändiga resurser för att köra T-portarna och T-fabrikerna avgörande för att fastställa algoritmens genomförbarhet. Azure Quantum Resource Estimator beräknar antalet T-tillstånd som behövs för att köra algoritmen, antalet fysiska kvantbitar för en enda T-fabrik och körningen av T-fabriken.
Universell uppsättning kvantgrindar
Enligt DiVincenzos kriterier måste en skalbar kvantdator kunna implementera en universell uppsättning kvantgrindar. En universell uppsättning innehåller alla portar som behövs för att utföra kvantberäkning, det vill ex. alla beräkningar måste delas upp i en fin sekvens av universella portar. En kvantdator måste åtminstone kunna flytta enskilda kvantbitar till valfri position på Bloch Sphere (med enstaka qubitgrindar) samt införa sammanflätning i systemet, vilket kräver en grind med flera kvantbitar.
Det finns bara fyra funktioner som mappar en bit till en bit på en klassisk dator. Det finns däremot ett oändligt antal enhetstransformeringar på en enda kvantbit på en kvantdator. Därför kan ingen begränsad uppsättning primitiva kvantåtgärder eller grindar exakt replikera den oändliga uppsättning enhetliga transformeringar som tillåts i kvantberäkning. Det innebär, till skillnad från klassisk databehandling, att det är omöjligt för en kvantdator att implementera alla möjliga kvantprogram exakt med hjälp av ett begränsat antal grindar. Kvantdatorer kan därför inte vara universella i samma bemärkelse som klassiska datorer. När vi säger att en uppsättning portar är universella för kvantberäkning menar vi därför faktiskt något något svagare än vad vi menar med klassisk databehandling.
För universalitet krävs det att en kvantdator endast ungefärliger varje enhetsmatris inom ett ändligt fel med hjälp av en begränsad längd på grindsekvensen.
Med andra ord är en uppsättning portar en universell grinduppsättning om någon enhetlig transformering kan skrivas ungefär som en produkt av grindar från denna uppsättning. Det krävs att det finns portar $G_{1}, G_{2}, \ldots, G_N$ från grinduppsättningen så att
$${G_N G_N-1}\cdots G_2 G_1 \ca U.$$
Eftersom konventionen för matris multiplikation är att multiplicera från höger till vänster är den första grindåtgärden i den här sekvensen, $G_N$, faktiskt den sista som tillämpas på kvanttillståndsvektorn. Mer formellt sägs en sådan grinduppsättning vara universell om det för varje feltolerans $\epsilon>0$ finns $G_1, \ldots, G_N$ så att avståndet mellan $G_N\ldots G_1$ och $U$ högst är $\epsilon$. Helst bör värdet för $N som behövs för att nå det här avståndet $\epsilon$ skalas poly-logaritmiskt med $1/\epsilon$$.
Till exempel är uppsättningen som bildas av Hadamard, CNOT och T-grindar en universell uppsättning, från vilken alla kvantberäkningar (på valfritt antal kvantbitar) kan genereras. Hadamard- och T-grinduppsättningen genererar en enda qubit-grind:
$$H=\frac{1}{\sqrt{ 1 amp; 1 \\ 1 &-1 \end{bmatrix}, \qquad T=\begin{bmatrix} 1 & 0 \\ 0 & e^{i\pi/4}\end{bmatrix}.&{2}}\begin{bmatrix} $$
I en kvantdator kan kvantgrindar klassificeras i två kategorier: Clifford-grindar och icke-Clifford-grindar, i det här fallet T-grinden. Kvantprogram som endast tillverkas av Clifford-portar kan simuleras effektivt med hjälp av en klassisk dator, och därför krävs icke-Clifford-grindar för att få kvantfördel. I många QEC-scheman (quantum error correction) är de så kallade Clifford-portarna lätta att implementera, det vill säga att de kräver mycket få resurser när det gäller åtgärder och kvantbitar för att implementera feltolerant, medan icke-Clifford-portar är ganska kostsamma när feltolerans krävs. I en universell kvantgrindsuppsättning används T-grinden ofta som icke-Clifford-grind.
Standarduppsättningen med Clifford-portar med enkel qubit, som ingår som standard i Q#, inkluderar
$$ H=\frac{{1}{\sqrt{{2}}\begin{bmatrix} 1 & 1 \\ 1 &-1 \end{bmatrix} , \qquad S =\begin{bmatrix} 1 & 0 \\ 0 & i \end{bmatrix}= T^2, \qquad X=\begin{bmatrix} 0 & 1 \\ 1& 0 \end{bmatrix}= HT^4H, $$
$$ Y =\begin{bmatrix} 0 & -i \\ i & 0 \end{bmatrix}=T^2HT^4 HT^6, \qquad Z=\begin{bmatrix}1& 0\\ 0&-1 \end{bmatrix}=T^4. $$
Tillsammans med icke-Clifford-grinden (T-grinden) kan dessa åtgärder bestå för att approximeras vid en enhetlig transformering på en enda kvantbit.
T-fabriker i Azure Quantum Resource Estimator
Förberedelsen av icke-Clifford T-grinden är avgörande eftersom de andra kvantgrindarna inte räcker till för universell kvantberäkning. För att implementera icke-Clifford-åtgärder för algoritmer i praktisk skala krävs T-portar med låg felfrekvens (eller T-tillstånd). De kan dock vara svåra att implementera direkt på logiska kvantbitar och kan också vara svåra för vissa fysiska kvantbitar.
I en feltolerant kvantdator produceras de nödvändiga låg felfrekvens-T-tillstånden med hjälp av en T-tillståndsdestillationsfabrik eller T-fabrik för kort. Dessa T-fabriker omfattar vanligtvis en sekvens av destillationsrundor, där varje runda tar in många bullriga T-tillstånd kodade i en mindre avståndskod, bearbetar dem med hjälp av en destillationsenhet och matar ut färre mindre bullriga T-tillstånd kodade i en större avståndskod, med antalet rundor, destillationsenheter och avstånd som alla är parametrar som kan varieras. Den här proceduren itereras, där utdata-T-tillstånden för en runda matas in i nästa runda som indata.
Baserat på varaktigheten för T-fabriken avgör Azure Quantum Resource Estimator hur ofta en T-fabrik kan anropas innan den överskrider den totala körningen av algoritmen och därmed hur många T-tillstånd som kan produceras under algoritmkörningen. Vanligtvis krävs fler T-tillstånd än vad som kan skapas inom anropen för en enda T-fabrik under algoritmkörningen. För att skapa fler T-tillstånd använder Resource Estimator kopior av T-fabrikerna.
Fysisk uppskattning av T-fabrik
Resource Estimator beräknar det totala antalet T-tillstånd som behövs för att köra algoritmen och antalet fysiska kvantbitar för en enda T-fabrik och dess körning.
Målet är att skapa alla T-tillstånd inom algoritmkörningen med så få T-fabrikskopior som möjligt. Följande diagram visar ett exempel på körningen av algoritmen och körningen av en T-fabrik. Du kan se att körningen av T-fabriken är kortare än algoritmens körning. I det här exemplet kan en T-fabrik destillera ett T-tillstånd. Två frågor uppstår:
- Hur ofta kan T-fabriken anropas före algoritmens slut?
- Hur många kopior av T-fabriksdestillationen krävs för att skapa det antal T-tillstånd som krävs under algoritmens körning?
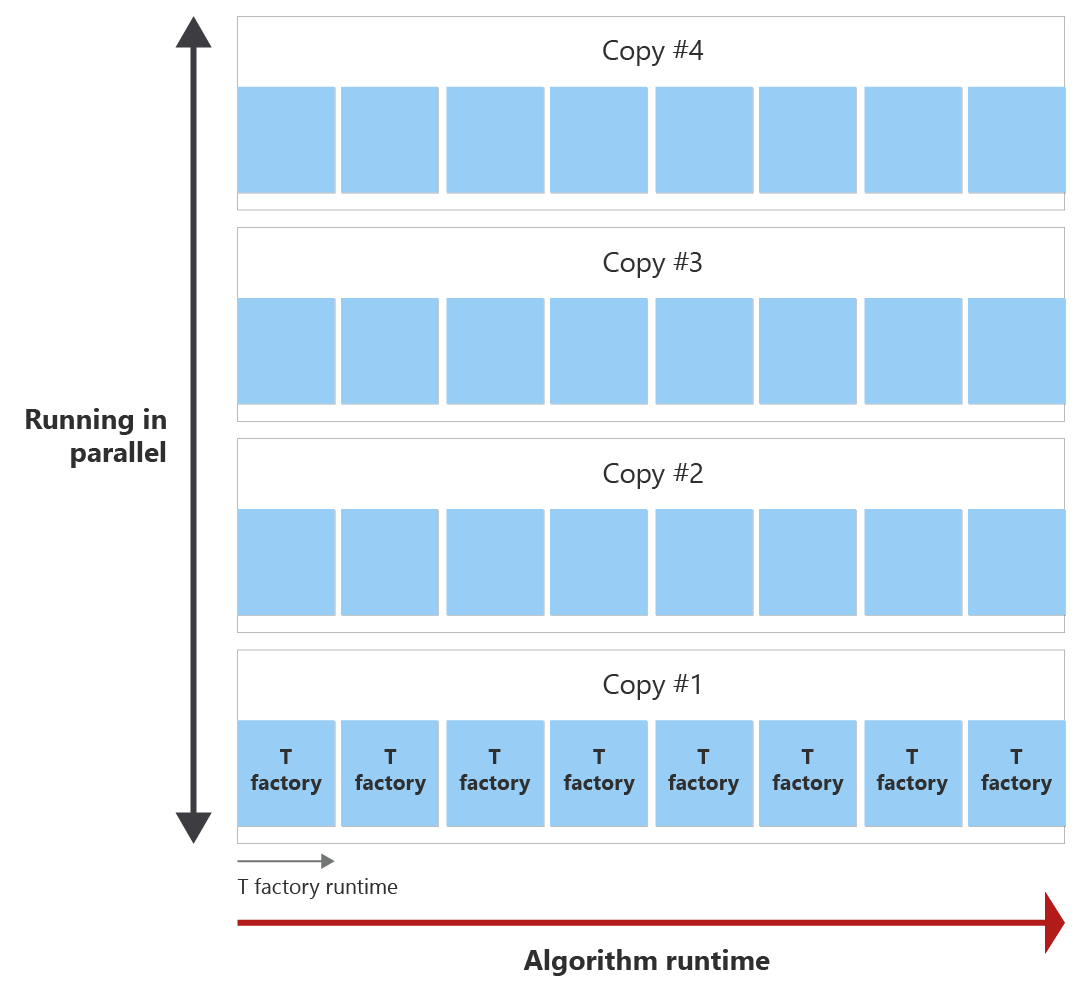
Innan algoritmen är slut kan T-fabriken anropas åtta gånger, vilket kallas för en destillationsrunda. Om du till exempel behöver 30 T-tillstånd anropas en enda T-fabrik åtta gånger under körningen av algoritmen och skapar därför åtta T-tillstånd. Sedan behöver du fyra kopior av T-fabriksdestillationen som körs parallellt för att destillera de 30 T-tillstånd som behövs.
Kommentar
Observera att T-fabrikskopior och T-fabriksanrop inte är desamma.
Destillationsfabrikerna för T-tillstånd implementeras i en sekvens av rundor, där varje runda består av en uppsättning kopior av destillationsenheter som körs parallellt. Resursberäknaren beräknar hur många fysiska kvantbitar som behövs för att köra en T-fabrik och hur länge T-fabriken körs, bland andra obligatoriska parametrar.
Du kan bara utföra fullständiga anrop av en T-fabrik. Det kan därför finnas situationer där den ackumulerade körningen av alla T-fabriksanrop är mindre än algoritmkörningen. Eftersom kvantbitar återanvänds av olika rundor är antalet fysiska kvantbitar för en T-fabrik det maximala antalet fysiska kvantbitar som används för en runda. Körningen av T-fabriken är summan av körningen i alla rundor.
Kommentar
Om felfrekvensen för den fysiska T-grinden är lägre än den nödvändiga logiska T-tillståndsfelfrekvensen kan resursberäknaren inte utföra en bra resursuppskattning. När du skickar ett resursuppskattningsjobb kan det hända att T-fabriken inte kan hittas eftersom felfrekvensen för det logiska T-tillståndet antingen är för låg eller för hög.
Mer information finns i Bilaga C till Bedömningskraven för att skala till praktisk kvantfördel.