Farklı kümeleme türlerini değerlendirme

• 5 dakika

Kümeleme modelini eğitma

Kümeleme için kullanabileceğiniz birden çok algoritma vardır. En yaygın kullanılan algoritmalardan biri, en basit biçimiyle aşağıdaki adımlardan oluşan K-Means kümelemedir:

1. Özellik değerleri, n boyutlu koordinatları tanımlamak için vektörleştirilir (burada n, özellik sayısıdır). Çiçek örneğinde iki özelliğimiz vardır: yaprakların sayısı ve yaprak sayısı. Bu nedenle özellik vektörde, veri noktalarını kavramsal olarak iki boyutlu alana çizmek için kullanabileceğimiz iki koordinat vardır.
2. Çiçekleri gruplandırmak için kaç küme kullanmak istediğinize karar verirsiniz; bu değeri k olarak adlandırın. Örneğin, üç küme oluşturmak için 3 k değeri kullanırsınız. Ardından k noktaları rastgele koordinatlara çizilir. Bu noktalar her küme için merkez noktalar haline gelir, bu nedenle bunlar centroid olarak adlandırılır.
3. Her veri noktası (bu örnekte bir çiçek) en yakın merkez merkezine atanır.
4. Her merkezkroid, noktalar arasındaki ortalama uzaklık temelinde kendisine atanan veri noktalarının merkezine taşınır.
5. Centroid taşındıktan sonra, veri noktaları artık farklı bir centroid'e daha yakın olabilir, bu nedenle veri noktaları yeni en yakın centroid temelinde kümelere yeniden atanır.
6. Kümeler kararlı hale gelene veya önceden belirlenmiş en fazla yineleme sayısına ulaşılana kadar centroid hareketi ve küme yeniden konumlandırma adımları yinelenir.

Aşağıdaki animasyonda bu işlem gösterilmektedir:

Hiyerarşik Kümeleme

Hiyerarşik kümeleme, kümelerin daha büyük gruplara ait olduğu ve daha büyük gruplara ait olduğu başka bir kümeleme algoritması türüdür. Sonuç olarak veri noktaları farklı duyarlık derecelerinde kümeler olabilir: çok fazla sayıda çok küçük ve hassas grup veya az sayıda daha büyük grup olabilir.

Örneğin, sözcüklerin anlamlarına kümeleme uygularsak, duygulara özgü sıfatlar içeren bir grup elde edebiliriz ('angry,' 'mutlu', vb.). Bu grup, tüm sıfatları ('mutlu,' 'yakışıklı,' 'genç') içeren ve tüm sıfatları ('mutlu,' 'yeşil,' 'yakışıklı,' 'sert' vb.) içeren daha da yüksek bir gruba ait.

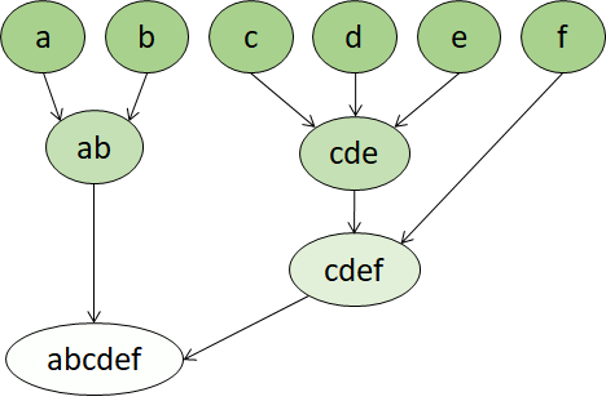
Hiyerarşik kümeleme yalnızca verileri gruplara bölmek için değil, aynı zamanda bu gruplar arasındaki ilişkileri anlamak için de yararlıdır. Hiyerarşik kümelemenin en önemli avantajlarından biri, küme sayısının önceden tanımlanmasını gerektirmemesidir. Ayrıca, bazen hiyerarşik olmayan yaklaşımlardan daha fazla yorumlanabilir sonuç sağlayabilir. En önemli dezavantajları, bu yaklaşımların daha basit yaklaşımlara göre daha uzun sürmesi ve bazen büyük veri kümeleri için uygun olmalarıdır.