Transformación de proyección (Direct3D 9)

  • Artículo

Puede pensar en la transformación de proyección como controlar los internos de la cámara; es análogo a elegir una lente para la cámara. Este es el más complicado de los tres tipos de transformación. Esta explicación de la transformación de proyección se organiza en los temas siguientes.

La matriz de proyección suele ser una proyección de escala y perspectiva. La transformación de proyección convierte el frustum de visualización en una forma cuboide. Dado que el extremo cercano del frustum de visualización es más pequeño que el extremo lejano, esto tiene el efecto de expandir objetos que están cerca de la cámara; así es como se aplica la perspectiva a la escena.

En el frustum de visualización, la distancia entre la cámara y el origen del espacio de transformación de visualización se define arbitrariamente como D, por lo que la matriz de proyección es similar a la ilustración siguiente.

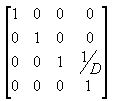
ilustración de la matriz de proyección

La matriz de visualización traduce la cámara al origen traduciéndolo en la dirección z por - D. La matriz de traducción es similar a la ilustración siguiente.

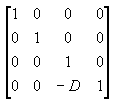
ilustración de la matriz de traducción

Multiplicar la matriz de traducción por la matriz de proyección (T*P) proporciona la matriz de proyección compuesta, como se muestra en la ilustración siguiente.

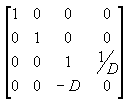
ilustración de la matriz de proyección compuesta

La transformación de perspectiva convierte un frustum de visualización en un nuevo espacio de coordenadas. Observe que el frustum se convierte en cuboide y también que el origen se mueve desde la esquina superior derecha de la escena al centro, como se muestra en el diagrama siguiente.

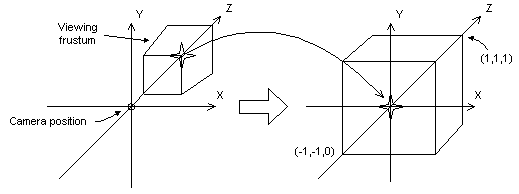
diagrama de cómo la transformación de perspectiva cambia el frustum de visualización en un nuevo espacio de coordenadas

En la transformación de perspectiva, los límites de las direcciones x e y son -1 y 1. Los límites de la dirección z son 0 para el plano delantero y 1 para el plano posterior.

Esta matriz traduce y escala objetos en función de una distancia especificada desde la cámara al plano de recorte cercano, pero no tiene en cuenta el campo de vista (fov) y los valores z que genera para los objetos en la distancia pueden ser casi idénticos, lo que dificulta las comparaciones de profundidad. La siguiente matriz soluciona estos problemas y ajusta los vértices para tener en cuenta la relación de aspecto de la ventanilla, lo que hace que sea una buena opción para la proyección de perspectiva.

ilustración de una matriz para la proyección de perspectiva

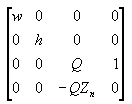
En esta matriz, Zn es el valor z del plano de recorte cercano. Las variables w, h y Q tienen los significados siguientes. Tenga en cuenta que fovw y fovk representan los campos horizontales y verticales de la ventanilla, en radianes.

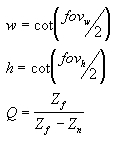
ecuaciones de los significados de la variable

Para la aplicación, es posible que el uso de ángulos de campo de vista para definir los coeficientes de escalado x e y no sea tan cómodo como usar las dimensiones horizontales y verticales de la ventanilla (en el espacio de la cámara). A medida que las matemáticas funcionan, las dos ecuaciones siguientes para w y h usan las dimensiones de la ventanilla y son equivalentes a las ecuaciones anteriores.

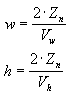
ecuaciones de los significados de la variable w y h

En estas fórmulas, Zn representa la posición del plano de recorte cercano y las variables Vw y Vh representan el ancho y el alto de la ventanilla, en el espacio de la cámara.

Para una aplicación de C++, estas dos dimensiones corresponden directamente a los miembros Width y Height de la estructura D3DVIEWPORT9 .

Sea cual sea la fórmula que decida usar, asegúrese de establecer Zn en un valor tan grande como sea posible, ya que los valores z extremadamente cercanos a la cámara no varían en gran medida. Esto hace comparaciones de profundidad con búferes z de 16 bits algo complicados.

Al igual que con las transformaciones de mundo y vista, llama al método IDirect3DDevice9::SetTransform para establecer la transformación de proyección.

Configuración de una matriz de proyección

La siguiente función de ejemplo ProjectionMatrix establece los planos de recorte frontal y trasero, así como el campo horizontal y vertical de ángulos de vista. Los campos de vista deben ser menores que pi radianes.

D3DXMATRIX 
ProjectionMatrix(const float near_plane, // Distance to near clipping 
                                         // plane
                 const float far_plane,  // Distance to far clipping 
                                         // plane
                 const float fov_horiz,  // Horizontal field of view 
                                         // angle, in radians
                 const float fov_vert)   // Vertical field of view 
                                         // angle, in radians
{
    float    h, w, Q;

    w = (float)1/tan(fov_horiz*0.5);  // 1/tan(x) == cot(x)
    h = (float)1/tan(fov_vert*0.5);   // 1/tan(x) == cot(x)
    Q = far_plane/(far_plane - near_plane);

    D3DXMATRIX ret;
    ZeroMemory(&ret, sizeof(ret));

    ret(0, 0) = w;
    ret(1, 1) = h;
    ret(2, 2) = Q;
    ret(3, 2) = -Q*near_plane;
    ret(2, 3) = 1;
    return ret;
}   // End of ProjectionMatrix

Después de crear la matriz, establézcala con IDirect3DDevice9::SetTransform especificando D3DTS_PROJECTION.

La biblioteca de utilidades D3DX proporciona las siguientes funciones para ayudarle a configurar la matriz de proyección.

Matriz de proyección compatible con W

Direct3D puede usar el componente w de un vértice transformado por el mundo, la vista y las matrices de proyección para realizar cálculos basados en profundidad en efectos de niebla o búfer de profundidad. Los cálculos como estos requieren que la matriz de proyección normalice w para que sea equivalente a world-space z. En resumen, si la matriz de proyección incluye un coeficiente (3,4) que no es 1, debe escalar todos los coeficientes por el inverso de (3,4) coeficiente para crear una matriz adecuada. Si no proporciona una matriz compatible, los efectos de niebla y el almacenamiento en búfer de profundidad no se aplican correctamente.

En la ilustración siguiente se muestra una matriz de proyección no compatible y la misma matriz escalada para que se habilite la niebla relativa a los ojos.

ilustraciones de una matriz de proyección no compatible y una matriz con niebla relativa a los ojos

En las matrices anteriores, se supone que todas las variables no son cero. Para obtener más información sobre la niebla relativa a los ojos, vea Profundidad relativa a los ojos frente a la profundidad basada en Z. Para obtener información sobre el almacenamiento en búfer de profundidad basado en w, vea Búferes de profundidad (Direct3D 9).

Direct3D usa la matriz de proyección establecida actualmente en sus cálculos de profundidad basados en w. Como resultado, las aplicaciones deben establecer una matriz de proyección compatible para recibir las características deseadas basadas en w, incluso si no usan Direct3D para las transformaciones.

Transformaciones