Convenzioni del diagramma del circuito quantistico
A volte gli algoritmi quantistici sono più facili da comprendere in un diagramma circuito rispetto alla rappresentazione di matrice scritta equivalente. Questo articolo illustra come leggere i diagrammi di circuito quantistico e le relative convenzioni.
Per altre informazioni, vedere Come visualizzare diagrammi di circuiti quantistici.
Lettura di diagrammi di circuito quantistico
In un circuito quantistico il tempo scorre da sinistra a destra. Le porte quantistiche vengono ordinate cronologicamente, quindi la porta più a sinistra è quella applicata per prima ai qubit.
Si prenda il diagramma del circuito quantistico seguente come esempio:
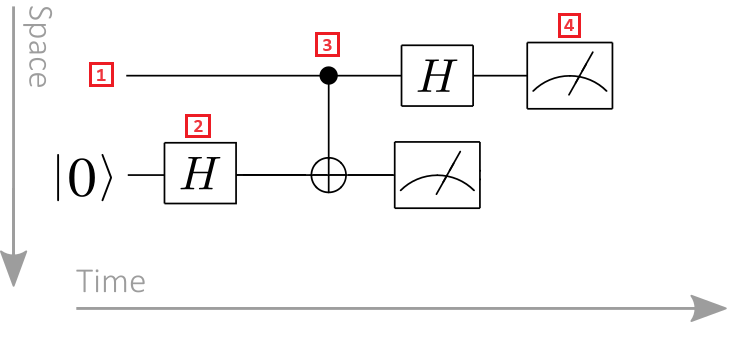
- Registro qubit: i registri qubit vengono visualizzati come linee orizzontali, con ogni riga che rappresenta un qubit. La riga superiore è il registro qubit con etichetta 0, la seconda riga è il registro qubit etichettato 1 e così via.
- Gate quantistico: le operazioni quantistiche sono rappresentate dai gate quantistici. Il termine porta quantistica è un'analogia con le porte logiche classiche. Le porte che agiscono su uno o più registri di qubit sono definite riquadri. In questo esempio il simbolo rappresenta un'operazione Hadamard.
- Gate controllato: i gate controllati agiscono su due o più qubit. In questo esempio il simbolo rappresenta un gate CNOT. Il cerchio nero rappresenta il qubit di controllo e la croce all'interno di un cerchio rappresenta il target qubit.
- Operazione di misurazione: il simbolo del contatore rappresenta un'operazione di misurazione. L'operazione di misurazione accetta un registro qubit come input e restituisce informazioni classiche.
Applicazione di gate quantistici
Poiché il tempo passa da sinistra a destra, il gate più a sinistra viene applicato per primo, ad esempio, l'azione del circuito quantistico seguente è l'autorità di certificazione della matrice $$unitaria.
Nota
La moltiplicazione della matrice rispetta la convenzione opposta: la matrice più a destra viene applicata per prima. Nei diagrammi dei circuiti quantistici, tuttavia, la porta più a sinistra viene applicata per prima. Questa differenza può a volte causare confusione, è quindi importante notare questa differenza significativa tra la notazione algebrica lineare e i diagrammi dei circuiti quantistici.
Input e output di circuiti quantistici
In un diagramma del circuito quantistico, i cavi che entrano in un gate quantistico rappresentano i qubit che sono input per il gate quantistico e i cavi che escono dal gate quantistico rappresentano i qubit restituiti dal gate quantistico.
Il numero di input di un gate quantistico è uguale al numero di output di un gate quantistico. Ciò è dovuto al fatto che le operazioni quantistiche sono unitarie e quindi reversibili. Se un gate quantistico avesse più output rispetto agli input, non sarebbe reversibile e quindi non unitario, che è una contraddizione.
Per questo motivo, qualsiasi riquadro disegnato in un diagramma del circuito deve avere esattamente lo stesso numero di linee in entrata e in uscita.
Operazioni multi qubit
I diagrammi dei circuiti a qubit multipli seguono convenzioni simili a quelle a qubit singolo. Ad esempio, un'operazione $unitaria a due qubit B$ può essere definita come $(H S\otimes X),$ quindi il circuito quantistico equivalente è il seguente:
È anche possibile visualizzare $B$ come un'azione su un singolo registro a due qubit anziché su due registri a un qubit, a seconda del contesto in cui viene usato il circuito.
La proprietà più utile di questi diagrammi dei circuiti astratti è forse che consentono di descrivere algoritmi quantistici complessi a livello generale senza doverli compilare fino alle porte fondamentali. Ciò significa che è possibile ottenere un'idea del flusso di dati per un algoritmo quantistico di grandi dimensioni senza dover comprendere tutti i dettagli del funzionamento di ognuna delle subroutine all'interno dell'algoritmo.
Porte controllate
I controlli quantistici sono gate a due qubit che applicano un gate a qubit singolo a un target qubit se un qubit di controllo si trova in uno stato specifico.
Si consideri ad esempio un gate controllato quantistico, indicato $\Lambda(G),$ in cui il valore di un singolo qubit controlla l'applicazione dell'operazione $G$ . Il gate $\Lambdacontrollato (G)$ può essere compreso esaminando l'esempio seguente di input dello stato del prodotto:
$\Lambda(G) (\alpha\ket{{0} + \beta\ket{1}) \ket{\psi}=\alpha\ket{{0}\ket{\psi} + \beta\ket{{1} G\ket{\psi}$
Vale a dire che la porta controllata applica $G$ al registro contenente $\psi$ se e solo se il qubit di controllo accetta il valore $1$. In generale, tali operazioni controllate sono descritte nei diagrammi di circuito con il simbolo seguente:
Qui il cerchio nero indica il bit quantistico su cui viene controllata la porta e una linea verticale indica l'unità applicata quando il qubit di controllo accetta il valore $1$.
Per i casi speciali in cui $G=X$ e $G=Z$, la notazione seguente viene usata per descrivere la versione controllata dei cancelli (si noti che il gate controllato-X è il gate CNOT):
Q# fornisce metodi per generare automaticamente la versione controllata di un'operazione, che consente al programmatore di non dover eseguire manualmente queste operazioni. Di seguito è illustrato un esempio di questa situazione:
operation PrepareSuperposition(qubit : Qubit) : Unit
is Ctl { // Auto-generate the controlled specialization of the operation
H(qubit);
}
Controlli classici controllati
I cancelli quantistici possono essere applicati anche dopo una misurazione, in cui il risultato della misurazione funge da bit di controllo classico.
Il simbolo seguente rappresenta un cancello controllato in modo classico, in cui $G$ viene applicato condizionale sul bit di controllo classico con valore $1$:
Operatore di misurazione
Le operazioni di misurazione accettano un registro qubit, la misura e restituisce il risultato come informazioni classiche.
Un'operazione di misurazione viene indicata da un simbolo del contatore e accetta sempre come input un registro di qubit (indicato da una linea continua) e restituisce informazioni classiche (indicate da una linea doppia). In particolare, il simbolo dell'operazione di misurazione è simile al seguente:
In Q#l'operatore Measure implementa l'operazione di misurazione.
Esempio: Trasformazione unitaria
Si consideri la trasformazione unitaria $\text{ CNOT}_{01}(H\otimes 1)$. Questa sequenza di porte è di fondamentale importanza per il calcolo quantistico perché crea uno stato a due qubit con entanglement massimo:
$\mathrm{CNOT}_{01}(H\otimes 1)\ket{00}=\frac{1}{\sqrt{2}}\left(\ket{{00} + \ket{11}\right),$
Le operazioni con questa o maggiore complessità sono onnipresenti negli algoritmi quantistici e nella correzione degli errori quantistici.
Il diagramma del circuito per la preparazione di questo stato quantistico con entanglement massimo è:
Il simbolo dietro il cancello hadamard rappresenta un cancello CNOT, dove il cerchio nero indica il qubit di controllo e la croce all'interno di un cerchio indica il target qubit. Questo circuito quantistico viene rappresentato come se agisse su due qubit (o, in modo equivalente, come due registri costituiti da un qubit).
Esempio: Diagramma del circuito di teleportazione
La teleportazione quantistica è uno dei migliori algoritmi quantistici per illustrare i componenti del circuito.
Il teletrasporto quantistico è un protocollo che consente di trasmettere uno stato quantistico da un qubit a un altro, con l'aiuto di uno stato entangled condiviso tra il mittente e il ricevitore e la comunicazione classica tra di essi.
Ai fini dell'apprendimento, il mittente viene chiamato Alice, il ricevitore viene chiamato Bob e il qubit da teletrasportare viene chiamato qubit del messaggio. Alice e Bob contengono un qubit ciascuno e Alice ha un qubit aggiuntivo che è il qubit del messaggio.
Il diagramma di circuito seguente illustra il protocollo di teletrasporto:
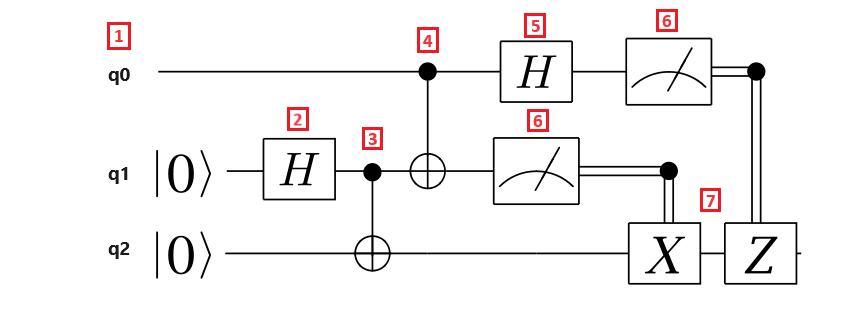
Di seguito sono descritti i passaggi del protocollo di teletrasporto:
- Qubit register q0 is the message qubit, qubit register q1 is Alice's qubit, and qubit register q2 is Bob's qubit. Il qubit del messaggio è in uno stato sconosciuto e i qubit di Alice e Bob si trovano nello $\ket{0}$ stato.
- Un cancello Hadamard viene applicato al qubit di Alice. Poiché il qubit è nello $\ket{0}$ stato , lo stato risultante è $\frac{1}{\sqrt{{2}}(\ket{{0} + \ket{1})$.
- Un gate CNOT viene applicato ai qubit di Alice e Bob. Il qubit di Alice è il qubit di controllo e il qubit di Bob è il target qubit. Lo stato risultante è $\frac{{1}{\sqrt{2}}(\ket{00} + \ket{{11})$. Alice e Bob ora condividono uno stato entangled.
- Un gate CNOT viene applicato al qubit del messaggio e al qubit di Alice. Poiché il qubit di Alice è anche entangled con il qubit di Bob, lo stato risultante è uno stato entangled a tre qubit.
- Un controllo Hadamard viene applicato al qubit del messaggio.
- Alice misura i due qubit e indica i risultati della misurazione a Bob, che non si riflette nel circuito. I risultati della misurazione sono due bit classici, che possono accettare i valori 00, 01, 10 o 11.
- Due gate Pauli X e Z controllati classicamente vengono applicati al qubit di Bob, a seconda del bit $di risultato 1$. Lo stato risultante è lo stato del qubit del messaggio originale.