Ruolo delle porte T e delle factory T nel calcolo quantistico
Questo articolo descrive il ruolo dei gate T e delle factory T nel calcolo quantistico a tolleranza di errore. Fornire un algoritmo quantistico, la stima delle risorse necessarie per l'esecuzione dei gate T e delle factory T diventa fondamentale per determinare la fattibilità dell'algoritmo. Azure Quantum Resource Estimator calcola il numero di stati T necessari per eseguire l'algoritmo, il numero di qubit fisici per una singola factory T e il runtime della factory T.
Set universale di gate quantistici
Secondo i criteri di DiVincenzo, un computer quantistico scalabile deve essere in grado di implementare un set universale di porte quantistico. Un set universale contiene tutte le porte necessarie per eseguire qualsiasi calcolo quantistico, ovvero qualsiasi calcolo deve scomporre in una sequenza limitata di porte universali. Come minimo, un computer quantistico deve essere in grado di spostare singoli qubit in qualsiasi posizione in Bloch Sphere (usando porte a qubit singolo), nonché introdurre entanglement nel sistema, che richiede un gate multi-qubit.
In un computer classico sono presenti solo quattro funzioni che consentono di eseguire il mapping da un bit a un bit. Al contrario, in un computer quantistico è presente un numero infinito di trasformazioni unitarie in un singolo qubit. Pertanto, nessun set finito di operazioni o cancelli quantistici primitivi può replicare esattamente il set infinito di trasformazioni unitari consentite nel calcolo quantistico. Ciò significa che, a differenza del calcolo classico, è impossibile per un computer quantistico implementare ogni possibile programma quantistico usando esattamente un numero finito di porte. I computer quantistici non possono quindi essere universali nello stesso senso dei computer classici. Di conseguenza, quando si dice che un set di porte è universale per il calcolo quantistico, in realtà si intende qualcosa di leggermente più debole rispetto al calcolo classico.
Per l'universalità, è necessario che un computer quantistico approssima ogni matrice unitaria all'interno di un errore finito usando una sequenza di gate di lunghezza limitata.
In altre parole, un set di porte è un set di porte universali se una trasformazione unitaria può essere scritta approssimativamente come prodotto di porte di questo set. È necessario che per qualsiasi limite di errore prescritto esistano cancelli $G_{1}, G_{2}, \ldots, G_N$ dal set di cancelli in modo che
$$ G_N G_{N-1}\cdots G_2 G_1 \approx U. $$
Poiché la convenzione per la moltiplicazione della matrice consiste nel moltiplicare da destra a sinistra la prima operazione di controllo in questa sequenza, $G_N$, è in realtà l'ultima applicata al vettore di stato quantistico. Più formalmente, tale set di porte è detto universale se per ogni tolleranza di errore $\epsilon>0$ esiste $G_1, \ldots, G_N$, in modo che la distanza tra $G_N\ldots G_1$ e $U$ sia al massimo $\epsilon$. Idealmente, il valore di $N$ necessario per raggiungere questa distanza di $\epsilon$ deve essere scalato in modo poli-logaritmico con $1/\epsilon$.
Ad esempio, il set formato da Hadamard, CNOT e T gates è un set universale, da cui è possibile generare qualsiasi calcolo quantistico (in qualsiasi numero di qubit). Il set di gate Hadamard e T genera qualsiasi gate a qubit singolo:
$$H=\frac{1}{\sqrt{ 1 amp; 1 \\ &-1 \end{bmatrix}, \qquad T=\begin{bmatrix} 1 & 0 0 \\ & e^{i\pi/4.\end{bmatrix}}&{2}}\begin{bmatrix} $$
In un computer quantistico, i cancelli quantistici possono essere classificati in due categorie: porte Clifford e porte non Clifford, in questo caso il cancello T. I programmi quantistici realizzati da sole porte Clifford possono essere simulati in modo efficiente usando un computer classico e pertanto, per ottenere il vantaggio quantistico sono necessari cancelli non Clifford. In molti schemi di correzione degli errori quantistici (QEC) i cosiddetti gate Clifford sono facili da implementare, ovvero richiedono pochissime risorse in termini di operazioni e qubit per implementare le porte a tolleranza di errore, mentre i cancelli non Clifford sono piuttosto costosi quando richiedono la tolleranza di errore. In un set di cancelli quantistici universali, il cancello T viene comunemente usato come porta non Clifford.
Il set standard di porte Clifford a qubit singolo, incluso per impostazione predefinita in Q#, include
$$H=\frac{{1}{\sqrt{{2}}\begin{bmatrix} 1 & 1 \\ 1 &-1 \end{bmatrix} , \qquad S =\begin{bmatrix} 1 & 0 0 &\\ amp; i \end{bmatrix}= T^2, \qquad X=\begin{bmatrix} 0 & 1 \\& 0 \end{bmatrix}= HT^4H,$$
$$Y =0 amp; -i &\\ amp; 0 \end{bmatrix}=T^2HT^4 HT^6, \qquad Z=\begin{bmatrix}1&&\begin{bmatrix} 0\\ 0&-1 \end{bmatrix}=T^4. $$
Insieme al gate non Clifford (il cancello T), queste operazioni possono essere composte per approssimare qualsiasi trasformazione unitaria su un singolo qubit.
T factory nello strumento di stima delle risorse di Azure Quantum
La preparazione del gate T non Clifford è fondamentale perché le altre porte quantistiche non sono sufficienti per il calcolo quantistico universale. Per implementare operazioni non Clifford per algoritmi pratici, sono necessari controlli T a bassa frequenza di errore (o T stati). Tuttavia, possono essere difficili da implementare direttamente nei qubit logici e possono anche essere difficili per alcuni qubit fisici.
In un computer quantistico a tolleranza di errore, gli stati T a bassa frequenza di errore richiesti vengono prodotti usando una fabbrica distillazione di stato T o T factory per brevità. Queste fabbriche T in genere comportano una sequenza di round distillato, in cui ogni round prende molti stati T rumorosi codificati in un codice di distanza più piccolo, li elabora usando un'unità di decodifica e restituisce meno stati T rumorosi codificati in un codice di distanza più grande, con il numero di round, unità di codifica e distanze che tutti sono parametri che possono essere diversi. Questa procedura viene iterata, in cui gli stati T di output di un round vengono inseriti nel round successivo come input.
In base alla durata della factory T, Lo strumento di stima delle risorse di Azure Quantum determina la frequenza con cui una factory T può essere richiamata prima che superi il runtime totale dell'algoritmo e quindi il numero di stati T che possono essere generati durante il runtime dell'algoritmo. In genere, sono necessari più stati T rispetto a quelli che possono essere generati all'interno delle chiamate di una singola factory T durante il runtime dell'algoritmo. Per produrre più stati T, lo strumento di stima delle risorse usa copie delle factory T.
Stima fisica della fabbrica T
Lo strumento di stima delle risorse calcola il numero totale di stati T necessari per eseguire l'algoritmo e il numero di qubit fisici per una singola factory T e il relativo runtime.
L'obiettivo è produrre tutti gli stati T all'interno del runtime dell'algoritmo con il minor numero possibile di copie factory T. Il diagramma seguente mostra un esempio del runtime dell'algoritmo e del runtime di una factory T. È possibile notare che il runtime della factory T è più breve del runtime dell'algoritmo. In questo esempio, una factory T può distillare uno stato T. Si presentano due domande:
- Con quale frequenza è possibile richiamare la factory T prima della fine dell'algoritmo?
- Quante copie del round di produzione T factory sono necessarie per creare il numero di stati T necessari durante il runtime dell'algoritmo?
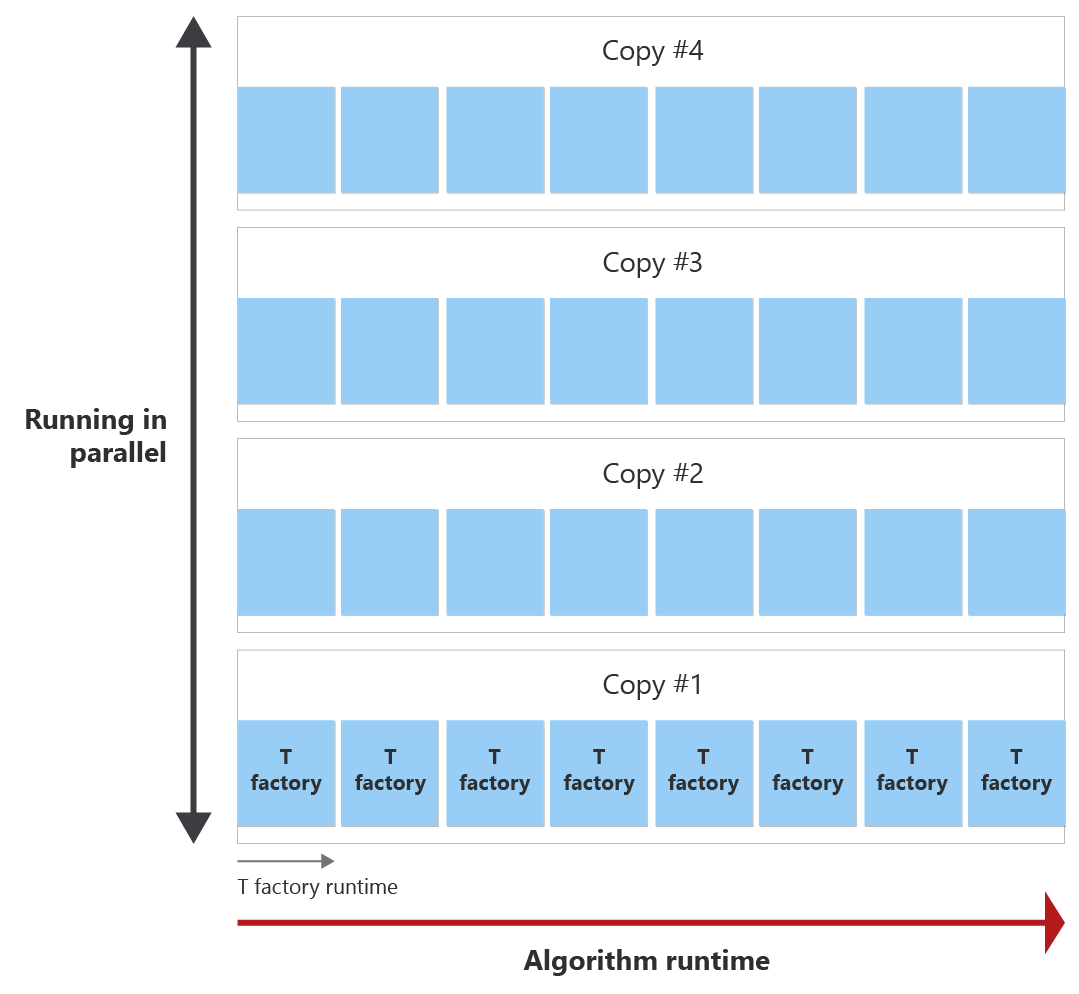
Prima della fine dell'algoritmo, la fabbrica T può essere richiamata otto volte, che viene chiamata round distillato. Ad esempio, se sono necessari 30 stati T, una singola factory T viene richiamata otto volte durante il runtime dell'algoritmo e quindi crea otto stati T. Quindi sono necessarie quattro copie del ciclo di esportazione della fabbrica T in parallelo per distillare gli stati 30 T necessari.
Nota
Si noti che le copie della factory T e le chiamate di fabbrica T non sono uguali.
Le fabbriche distillato dello stato T vengono implementate in una sequenza di arrotondamenti, dove ogni round è costituito da un set di copie di unità di copia in esecuzione in parallelo. Lo strumento di stima delle risorse calcola il numero di qubit fisici necessari per eseguire una factory T e per quanto tempo viene eseguita la factory T, tra gli altri parametri obbligatori.
È possibile eseguire chiamate complete solo di una factory T. Di conseguenza, possono verificarsi situazioni in cui il runtime accumulato di tutte le chiamate di fabbrica T è minore del runtime dell'algoritmo. Poiché i qubit vengono riutilizzati da round diversi, il numero di qubit fisici per una factory T è il numero massimo di qubit fisici usati per un round. Il runtime della factory T è la somma del runtime in tutti i round.
Nota
Se la frequenza degli errori di controllo T fisico è inferiore alla frequenza di errore dello stato T logico richiesto, lo strumento di stima delle risorse non può eseguire una stima valida delle risorse. Quando si invia un processo di stima delle risorse, è possibile che non sia possibile trovare la factory T perché la frequenza di errore dello stato T logico richiesto è troppo bassa o troppo elevata.
Per altre informazioni, vedere Appendice C della valutazione dei requisiti per la scalabilità a vantaggi quantistici pratici.