Ipotesi di test usando t-test
Importante
Il supporto dello studio di Azure Machine Learning (versione classica) terminerà il 31 agosto 2024. È consigliabile passare ad Azure Machine Learning entro tale data.
A partire dal 1° dicembre 2021 non sarà possibile creare nuove risorse dello studio di Azure Machine Learning (versione classica). Fino al 31 agosto 2024 sarà possibile continuare a usare le risorse dello studio di Azure Machine Learning (versione classica).
- Vedere leinformazioni sullo spostamento di progetti di Machine Learning da ML Studio (versione classica) ad Azure Machine Learning.
- Altre informazioni sulle Azure Machine Learning.
La documentazione relativa allo studio di Machine Learning (versione classica) è in fase di ritiro e potrebbe non essere aggiornata in futuro.
Confronta i mezzi da due colonne usando un t-test
Categoria: Funzioni statistiche
Nota
Si applica a: solo Machine Learning Studio (versione classica)
I moduli di trascinamento e rilascio simili sono disponibili in Azure Machine Learning finestra di progettazione.
Panoramica del modulo
Questo articolo descrive come usare il modulo Test Ipotesi usando t-Test in Machine Learning Studio (versione classica) per generare punteggi per tre tipi di t-test:
- Test t su campione singolo
- Test t appaiato
- Test t non appaiato
In generale, un test t consente di confrontare due gruppi per vedere se hanno medie differenti. Si supponga, ad esempio, di valutare i dati di uno studio clinico per pazienti ai quali è stato somministrato il farmaco A rispetto a quelli ai quali è stato somministrato il farmaco B e di voler confrontare la metrica relativa al tasso di guarigione per entrambi i gruppi. L'ipotesi Null presuppone che il tasso di guarigione sia identico in entrambi i gruppi e che i valori corrispondenti abbiano una normale distribuzione in entrambi i gruppi.
Usando Test Ipotesi usando t-Test e fornendo le colonne che contengono i tassi di recupero come input, è possibile ottenere punteggi che indicano se la differenza è significativa, che indica che l'ipotesi null deve essere rifiutata. Il test prende in considerazione fattori quali l'entità della differenza tra i valori, le dimensioni del campione (più grande è, meglio è) e l'entità della deviazione standard (minore è, meglio è).
Esaminando i risultati del modulo Test Ipotesi usando t-Test , è possibile determinare se l'ipotesi null è TRUE o FALSE e esaminare i punteggi di attendibilità (P) dal t-test.
Come scegliere un t-test
Scegliere un singolo t-test di esempio quando si applicano queste condizioni:
Si dispone di un singolo campione di punteggi.
Tutti i punteggi sono indipendenti tra loro.
La distribuzione di campionamento di xˉ è normale.
In generale, il test t su campione singolo viene usato per confrontare un valore medio con un numero noto.
Scegliere un t-test associato quando si applicano queste condizioni:
Si dispone di coppie appaiate di punteggi. Ad esempio, si potrebbero avere due misure diverse per ogni persona oppure coppie appaiate di individui, come marito e moglie.
Ogni coppia di punteggi è indipendente dalle altre coppie.
La distribuzione di campionamento di d è normale.
Un test t appaiato è utile durante il confronto di casi correlati. Calcolando la media dei punteggi dei casi appaiati, è possibile determinare se la differenza totale è statisticamente rilevante.
Scegliere un t-test non abbinato quando si applicano queste condizioni:
Si dispone di due campioni indipendenti di punteggi. Ovvero, non esistono presupposti per appaiare i punteggi del campione 1 con quelli del campione 2.
Tutti i punteggi all'interno di un campione sono indipendenti da tutti gli altri punteggi all'interno dello stesso campione.
La distribuzione di campionamento di x1- x2 è normale.
Facoltativamente, è possibile soddisfare il requisito in base al quale la varianza tra gruppi deve essere all'incirca uguale.
Come configurare l'ipotesi di test usando t-test
Usare un singolo set di dati come input. Le colonne confrontate devono trovarsi nello stesso set di dati.
Se è necessario confrontare colonne da set di dati diversi, è possibile isolare ogni colonna da confrontare usando Select Columns in Dataset e quindi unire le colonne in un set di dati usando Aggiungi colonne.
Aggiungere il modulo Test Ipotesi usando t-Test all'esperimento.
È possibile trovare questo modulo nella categoria Funzioni statistiche in Studio (versione classica).
Aggiungere il set di dati contenente la colonna o le colonne da analizzare.
Decidere quale tipo di t-test è appropriato per i dati. Vedere Come scegliere un t-test.
Singolo esempio: se si usa un singolo esempio, impostare questi parametri:
Null ipotesi μ: digitare il valore da usare come media ipotesata null per l'esempio. In questo modo viene specificato il valore medio previsto rispetto al quale verrà testata la media di esempio.
Colonna di destinazione: usare il selettore di colonne per scegliere una singola colonna numerica per il test.
Tipo di ipotesi: scegliere un test a una coda o a due code. Il tipo predefinito è il test a due code. Si tratta del tipo di test più comune, in cui la distribuzione prevista è simmetrica intorno allo zero.
L'opzione One Tail GT è per un valore maggiore di quello di test. Questo test offre più potenza per rilevare un effetto in una direzione, non testando l'effetto nell'altra direzione.
L'opzione One Tail LT offre un test inferiore a una coda.
α: specificare un fattore di attendibilità. Questo valore viene usato per valutare il valore di P (il primo output del modulo). Se p è inferiore al fattore di attendibilità, l'ipotesi Null viene rifiutata.
PairedSamples: se si confrontano due campioni dalla stessa popolazione, impostare questi parametri:
Null ipotesi μ: digitare un valore che rappresenta la differenza di esempio tra la coppia di campioni.
Colonna di destinazione: usare il selettore di colonne per scegliere le due colonne numeriche da testare.
Tipo di ipotesi: selezionare un test a una coda o a due code. Il tipo predefinito è il test a due code.
α: specificare il fattore di attendibilità. Questo valore viene usato per valutare il valore di P (il primo output del modulo)> Se p è inferiore al fattore di attendibilità, l'ipotesi Null viene rifiutata.
UnpairedSamples: se si confrontano due esempi non abbinati, impostare questi parametri:
- Presupporre la varianza uguale: deselezionare questa opzione quando gli esempi provengono da popolazioni diverse.
- Null ipotesi μ1: digitare la media per la prima colonna.
- Null ipotesi μ2: digitare la media per la seconda colonna.
- Colonne di destinazione: usare il selettore di colonne per scegliere due colonne numeriche da testare.
- Tipo di ipotesi: indica se il test è a una coda o a due code. Il tipo predefinito è il test a due code.
- α: specificare il fattore di attendibilità. Questo valore viene usato per valutare il valore di P (il primo output del modulo)> Se p è inferiore al fattore di attendibilità, l'ipotesi Null viene rifiutata.
Eseguire l'esperimento.
Risultati
L'output del modulo è un set di dati contenente i punteggi t-test e una trasformazione che è possibile salvare facoltativamente per applicare nuovamente a questo o un altro set di dati usando Applica trasformazione.
Il set di dati dei punteggi contiene questi valori, indipendentemente dal tipo di t-test usato:
- Punteggio di probabilità che indica il livello di confidenza dell'ipotesi Null.
- Valore che indica se l'ipotesi Null deve essere rifiutata.
Suggerimento
Tenere presente che l'obiettivo consiste nel determinare se è possibile rifiutare l'ipotesi Null. Un punteggio pari a 0 non significa che è consigliabile accettare l'ipotesi Null: significa che non si hanno dati sufficienti e sono necessarie ulteriori indagini.
Note tecniche
Il modulo denomina automaticamente le colonne di output in base alle convenzioni seguenti, a seconda del tipo di test t selezionato e del fatto che il risultato determini l'accettazione o il rifiuto dell'ipotesi Null.
Le colonne di input specificate con nomi {0} e {1}, il modulo crea i nomi seguenti:
| Colonne | SingleSampleSet | PairedSamples | UnpairedSamples |
|---|---|---|---|
| Colonna di output P | P_ss({0}) | P_ps({0}, {1}) | P_us({0}, {1}) |
| Colonna di output RejectH0 | RejectH0_ss({0})" | RejectH0_ps({0}, {1}) | RejectH0_us({0}, {1}) |
Come vengono calcolati i punteggi
Questo modulo calcola e usa la deviazione standard di esempio; pertanto, l'equazione usa (n-1) nel denominatore.
Punteggi di calcolo per un test di esempio singolo
Supponendo un singolo campione di punteggi, tutti indipendenti gli uni dagli altri, e una distribuzione normale, il punteggio viene calcolato in questo modo:
Usare l'input seguente:
- Singola colonna di valori dal set di dati
- L'ipotesi Null (H0) parametro μ0
- Punteggio di attendibilità specificato da α
Estrarre il numero di campioni (n).
Calcolare la media dei dati campione.
Calcolare la deviazione standard (s) dei dati di esempio.
Calcolare t e gradi di libertà (df):
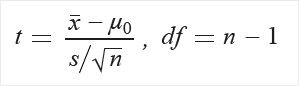
Estrarre probabilità P dalla tabella di distribuzione T usando t e df.
Punteggi di calcolo per un t-test associato
Supponendo un set appaiato di punteggi, con ogni coppia indipendente dall'altra, e una distribuzione normale in ogni set, il punteggio viene calcolato in questo modo:
Usare l'input seguente:
- Due colonne di valori dal set di dati
- L'ipotesi Null (H0) parametro d0
- Punteggio di attendibilità specificato da α
Estrarre un numero di coppie di esempio (n).
Calcolare la media delle differenze per i dati campione:
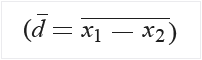
Calcolare la deviazione standard delle differenze (sd).
Calcolare t e i gradi di libertà (df):
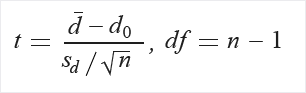
Estrarre probabilità (P) dalla tabella di distribuzione (T) usando t e df.
Punteggi di calcolo per un t-test non abbinato
Supponendo due campioni indipendenti di punteggi, con una distribuzione normale dei valori in ciascuno, il punteggio viene calcolato in questo modo:
Usare l'input seguente:
- Set di dati che contiene due colonne di
doubles - Parametro null (H0) (d0)
- Punteggio di attendibilità specificato da α
- Set di dati che contiene due colonne di
Estrarre un numero di esempi in ogni gruppo, n1 e n2.
Calcolare le medie per ognuno dei set di campioni.
Calcolare la deviazione standard per ogni gruppo come s1 e s2.
Calcolare t e gradi di libertà (df):
Facoltativamente, è possibile soddisfare il requisito per cui la varianza tra i gruppi debba essere all'incirca uguale:
Calcolare prima la deviazione standard raggruppata:
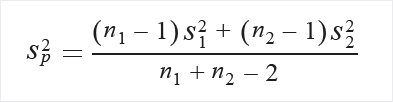
Se non esiste alcun presupposto sull'uguaglianza delle varianze, calcolare in questo modo:
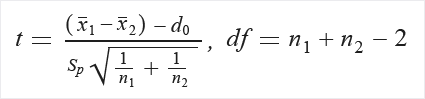
Estrarre P dalla tabella di distribuzione (T) usando t e df.
Calcolo dell'ipotesi null
La probabilità dell'ipotesi Null, designata come P, viene calcolata come segue:
Se P < α, impostare il flag Di rifiuto su True.
Se P ≥ α, impostare il flag Di rifiuto su False.
Input previsti
| Nome | Tipo | Descrizione |
|---|---|---|
| Set di dati | Tabella dati | Set di dati di input |
Parametri del modulo
| Name | Intervallo | Type | Predefinito | Descrizione |
|---|---|---|---|---|
| Hypothesis type | Qualsiasi | Hypothesis | A due code | Tipo di ipotesi Null del test t di Student |
| Ipotesi null μ | Qualsiasi | Float | 0.0 | Per il test t su campione singolo, media con ipotesi Null per il campione Per il test t appaiato, differenza dei campioni |
| Target column(s) | Qualsiasi | ColumnSelection | Nessuno | Criterio di selezione delle colonne di destinazione |
| Assume equal variances | Qualsiasi | Boolean | True | Si presuppone che le varianze dei due campioni siano uguali Si applica solo a campioni non appaiati |
| Null ipotesi μ1 | Qualsiasi | Float | 0.0 | Media con ipotesi nulla per il primo campione |
| Α | [0,0;1,0] | Float | 0.95 | Fattore di confidenza (se P è inferiore al fattore di confidenza, l'ipotesi Null viene rifiutata) |
Output
| Nome | Tipo | Descrizione |
|---|---|---|
| P | Tabella dati | Punteggio di probabilità che indica il livello di confidenza dell'ipotesi Null. |
| Rifiuto H0 | Tabella dati | Valore che indica se l'ipotesi Null deve essere rifiutata |
Eccezioni
| Eccezione | Descrizione |
|---|---|
| Errore 0003 | L'eccezione si verifica se uno o più input sono null o vuoti. |
| Errore 0008 | L'eccezione si verifica se il parametro non rientra nell'intervallo. |
| Errore 0017 | Si verifica un'eccezione se il tipo di una o più colonne specificate non è supportato dal modulo attuale. |
| Errore 0020 | Si verifica un'eccezione se il numero di colonne in alcuni set di dati passati al modulo è troppo piccolo. |
| Errore 0021 | Si verifica un'eccezione se il numero di righe in alcuni set di dati passati al modulo è troppo piccolo. |
| Errore 0031 | Si verifica un'eccezione se il numero di colonne nel set di colonne è inferiore al necessario. |
| Errore 0032 | Si verifica un'eccezione se l'argomento non è un numero. |
| Errore 0033 | Si verifica un'eccezione se l'argomento è un valore infinito. |
Per un elenco degli errori specifici dei moduli di Studio (versione classica), vedere Machine Learning Codici di errore.
Per un elenco delle eccezioni API, vedere Machine Learning codici di errore dell'API REST.