確率関数の評価
重要
Machine Learning Studio (クラシック) のサポートは、2024 年 8 月 31 日に終了します。 その日までに、Azure Machine Learning に切り替えすることをお勧めします。
2021 年 12 月 1 日以降、新しい Machine Learning Studio (クラシック) リソースは作成できません。 2024 年 8 月 31 日まで、既存の Machine Learning Studio (クラシック) リソースを引き続き使用できます。
- ML Studio (クラシック) から Azure Machine Learning への機械学習プロジェクトの移動に関する情報を参照してください。
- Azure Machine Learning についての詳細を参照してください。
ML Studio (クラシック) のドキュメントは廃止予定であり、今後更新されない可能性があります。
指定した確率分布関数をデータセットに適合させます
カテゴリ: 統計関数
注意
適用対象: Machine Learning Studio (クラシック) のみ
類似のドラッグ アンド ドロップ モジュールは Azure Machine Learning デザイナーで使用できます。
モジュールの概要
この記事では、Machine Learning Studio (クラシック) で確率関数の評価モジュールを使用して、ベルヌーイ分布、パレート分布、ポアソン分布などの列の分布を記述する統計メジャーを計算する方法について説明します。
このモデルを使用するには、数値の少なくとも 1 つの列を含むデータセットを接続し、テストする確率分布を選択します。 モジュールは、指定された確率関数の値を含むデータ テーブルを返します。
選択した確率分布に対して、次のいずれかの値を計算できます。
- 累積分布関数 (cdf)
- 逆累積分布関数 (InverseCdf)
- 確率密度関数 (Pdf)
確率分布が役立つのはなぜですか?
確率分布に対してデータを評価する場合、既知のプロパティを持つ一連の値に対して列値をマッピングします。 データがこれらの既知の分布のいずれかに対応しているかどうかを知ることで、データの他のプロパティを推測できる場合があります。 通常、データに最も適合する分布を特定できると、モデルからより精度の高い予測を得ることができます。
使用する確率分布関数は、測定するデータと変数に応じて決まります。 たとえば、一部の分布は、離散値の確率を記述するように設計されています。その他は、連続する数値変数でのみ使用することを目的としています。 一部の分布では、期待される平均や自由度などを事前に把握しておく必要があります。 詳細については、「サポートされる確率分布」を参照してください。
確率関数の評価を構成する方法
すべてのオプションは、計算する確率分布の種類によって変わります。 確率分布方法を変更すると、行ったその他の選択内容がリセットされる可能性があります。
したがって、必ず最初に [配布 ] オプションを選択してください。
入力として使用されるデータセットには、数値データが含まれている必要があります。 他の種類のデータは無視されます。
分析ごとに、1 つの確率分布方法を適用できます。 異なる確率分布を計算するには、テストするディストリビューションごとにモジュールの個別のインスタンスを追加します。
確率の 評価関数 モジュールを実験に追加します。 このモジュールは、Machine Learning Studio (クラシック) の統計関数カテゴリにあります。
少なくとも 1 つの数値列を含むデータセットをConnectします。
[分布] オプションを使用して、計算する確率分布の種類を選択します。 オプションとその必要な引数の一覧については、「 サポートされる確率分布 」を参照してください。
分布に必要なパラメーターを設定します。
作成する 3 つの統計のいずれかを選択します。累積分布関数 (cdf)、逆累積分布関数 (InverseCdf)、確率密度関数 (pdf)。
列セレクターを使用して、選択した確率分布を計算する列を選択します。
選択するすべての列には数値データ型が必要です。
確率関数が選択されている場合は、列のデータの範囲も有効である必要があります。 有効でない場合、エラーまたは NaN が発生する可能性があります。
スパース列の場合、バックグラウンドのゼロに対応する値はいずれも処理されません。
結果モード オプションを使用して、結果の出力方法を指定します。 列の値を確率分布値に置き換えて、そのデータセットに新しい値を追加するか、確率分布値のみを返すことができます。
実験を実行するか、[ 確率の評価] 関数 モジュールを右クリックし、[ 実行] をクリックします。
結果
次の表に、Forest Fires サンプル データセットの 1 つの温度列の [追加] オプションを使用した結果の例を示します。
| temp | StandardNormal.Cdf(temp) | StandardNormal.Pdf(temp) | FFisher.cdf(temp | FFisher.cdf(temp |
|---|---|---|---|---|
| 8.2 | 1 | 1 | 0.984774 | 0.004349 |
| 18 | 1 | 1 | 0.997896 | 0.000311 |
| 14.6 | 1 | 1 | 0.996352 | 0.000648 |
| 8.3 | 1 | 1 | 0.985201 | 0.004187 |
| 11.4 | 1 | 1 | 0.993147 | 0.001502 |
生成された列の見出しには、使用された確率分布が含まれています。
データに適している確率分布がわからない場合は、数値列の累積分布と確率密度のクイック チャートを作成できます。
- データセットまたはモジュールの出力を右クリックし、[ 視覚化] を選択します。
- 目的の列を選択し、[ ヒストグラム ] ウィンドウで累積 分布 または 確率密度を選択します。
- 次のような分布のグラフは、データを表すヒストグラムに重ね合わされます。
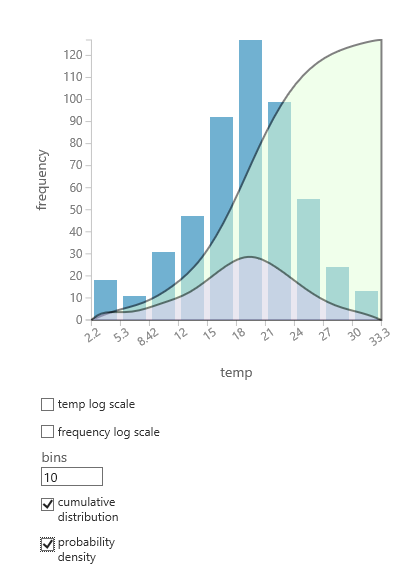
サポートされる確率分布
確率評価関数モジュールでは、次の分布がサポートされています。
ベルヌーイ
Bernoulli 分布は、バイナリ値に対する分布です。つまり、2 つの値のみが可能な場合に予測される分布をモデル化します。
計算するには、 Bernoulli を選択し、次のオプションを設定します。
- 成功率
パラメーター p は、1 が生成される確率を指定します。 成功率を指定する 0.0 ~ 1.0 の数値 (float) を入力します。 既定値は .5 です。
Beta
ベータ分布は、連続一変量分布です。
計算するには、[ ベータ] を選択し、次のオプションを設定します。
図形
値を入力して、分布の形状を変更します。形状のパラメーターは、形状の位置またはスケールを定義しない、確率分布のパラメーターです。 そのため、形状の値を入力すると、パラメーターは分布を移動したり、拡大または縮小したりするのではなく、分布の形状を変更します。
値は数値 (
double) である必要があります。 既定値は 1.0 です。スケール
分布のスケーリングで使用する数値を入力します。スケールの値を分布に適用すると、分布を縮小または拡大できます。
既定値は 1.0 です。 値は正の数値にする必要があります。
上限
分布の上限を表す数値 (double) を入力します。 既定値は 1.0 です。下限
分布の下限を表す数値 (double) を入力します。 既定では、0.0 です。
二項
二項分布は、離散一変量分布です。 サンプルでの成功の数をモデル化するには、二項分布を使用します。 置換はサンプリング時に使用されます。 置換を行わないサンプリングの場合は、超幾何分布を使用します。
計算するには、 二項を選択し、次のオプションを設定します。
成功率
成功率を示す 0.0 ~ 1.0 の数値 (float) を入力します。 既定値は .5 です。試行回数
試行回数を指定します。最小値が
integer1 の 、を使用します。 既定値は 3 です。
コーシー
コーシー分布は、対称性を持つ連続確率分布です。
計算するには、 Cauchy を選択し、次のオプションを設定します。
場所
0番目の要素の位置を表す数値 (double) を入力します。Location パラメーターの値を指定して、確率分布を数値スケールの上下へ移動することができます。
既定では、0.0 です。
カイ二乗
カイ二乗分布は、k 独立変数、標準変数、正規変数、ランダム変数の 2 乗の合計です。
計算するには、[ ChiSquare] を選択し、次のオプションを設定します。
- 自由度の数 自由度を指定するには、数値 (
double) を入力します。 既定値は 1.0 です。
ChiSquareRightTailed
このオプションは、右尾のカイ二乗分布を提供します。
計算するには、 ChiSquareRightTailed を選択し、次のオプションを設定します。
- 自由度数
自由度を指定する数値doubleを入力します。 既定値は 1.0 です。
指数
指数分布は、1 つの負以外のパラメーターでパラメーター化された実数に関する分布です。
計算するには、[ 指数] を選択し、次のオプションを設定します。
- Lambda
数値 (double) を入力して、ラムダ パラメーターとして使用します。 既定値は 1.0 です。
FFisher
サンプル (フィッシャー F 分布とも呼ばれます) のフィッシャー統計量の確率を生成します。 この配布は両側です。
計算するには、 FFisher を選択し、次のオプションを設定します。
分子の自由度
数値 (double) を入力し、分子で使用される自由度を指定します。 既定値は 3.0 です。分母の自由度
数値 (double) を入力し、分母で使用される自由度を指定します。 既定値は 6.0 です。
FFisherRightTailed
右尾のフィッシャー分布を作成します。 フィッシャー分布は、フィッシャー F 分布、スネデカー分布またはフィッシャー - スネデカー分布とも呼ばれます。 分布のこの特定の形式は右側です。
計算するには、 FFisherRightTailed を選択し、次のオプションを設定します。
分子の自由度
数値 (double) を入力し、分子で使用される自由度を指定します。 既定値は 3.0 です。分母の自由度
数値 (double) を入力し、分母で使用される自由度を指定します。 既定値は 6.0 です。
Gamma
ガンマ分布は、2 つのパラメーターの継続的な確率分布の一群です。 たとえば、カイ二乗は、ガンマ分布の特殊なケースです。
計算するには、[ ガンマ] を選択し、次のオプションを設定します。
スケール
分布のスケーリングで使用する値を入力します。スケールの値を分布に適用すると、分布を縮小または拡大できます。
既定値は 1.0 です。 値は正の数値にする必要があります。
場所
0番目の要素の位置を表す数値 (double) を入力します。Location パラメーターの値を指定して、確率分布を数値スケールの上下へ移動することができます。
既定では、0.0 です。
GeneralizedExtremeValues
極端な値を処理するために開発された分布を作成します。 一般極値 (GEV) 分布は、実際には、ガンベル、フレシェ、およびワイブル分布を合わせた連続確率分布のグループ (タイプ I、II、III の極値分布とも呼ばれます) です。
極値理論の詳細については、ウィキペディアの「 フィッシャー・ティペット・グネデンコ定理」の記事を参照してください。
計算するには、[ 一般化されたExtremeValues] を選択し、次のオプションを設定します。
図形
値を入力して、分布の形状を変更します。形状のパラメーターは、形状の位置またはスケールを定義しない、確率分布のパラメーターです。 そのため、形状の値を入力すると、パラメーターは分布を移動したり、拡大または縮小したりするのではなく、分布の形状を変更します。
値は数値 (
double) である必要があります。 既定値は 1.0 です。スケール
分布のスケーリングで使用する値を入力します。スケールの値を分布に適用すると、分布を縮小または拡大できます。
既定値は 1.0 です。 値は正の数値にする必要があります。
場所
0番目の要素の位置を表す数値 (double) を入力します。Location パラメーターの値を入力して、確率分布を数値スケールの上下へ移動することができます。
既定では、0.0 です。
幾何
幾何学的分布は、正の実数でパラメーター化された正の整数に対する分布です。
計算するには、[ ジオメトリック] を選択し、次のオプションを設定します。
- 成功率
成功率を示す 0.0 ~ 1.0 の数値 (float) を入力します。 既定値は .5 です。
注意
この幾何学的分布の実装では、ゼロは生成されません。
GumbelMax
ガンベル分布は、いくつかある極値分布の 1 つです。 [GumbelMax] オプションは、最大極値タイプ 1 分布を実装しています。
計算するには、 GumbelMax を選択し、次のオプションを設定します。
スケール
分布のスケーリングで使用する値を入力します。スケールの値を分布に適用すると、分布を縮小または拡大できます。
既定値は 1.0 です。 値は正の数値にする必要があります。
場所
0番目の要素の位置を表す数値 (double) を入力します。Location パラメーターの値を入力して、確率分布を数値スケールの上下へ移動することができます。
既定では、0.0 です。
GumbelMin
ガンベル分布は、いくつかある極値分布の 1 つです。 ガンベル分布は、最小極値 (SEV) 分布または最小極値 (タイプ I) 分布とも呼ばれます。 GumbelMin オプションは、最小極値タイプ 1 分布を実装します。
計算するには、 GumbelMin を選択し、次のオプションを設定する必要があります。
スケール
分布のスケーリングで使用する値を入力します。スケールの値を分布に適用すると、分布を縮小または拡大できます。
既定値は 1.0 です。 値は正の数値にする必要があります。
場所
0番目の要素の位置を表す数値 (double) を入力します。Location パラメーターの値を入力して、確率分布を数値スケールの上下へ移動することができます。
既定では、0.0 です。
超幾何
超幾何分布は、二項分布が置換を伴う描画の成功数を記述するのと同様に、置換を伴わない有限母集団からの n 個の描画のシーケンスにおける成功数を記述する離散確率分布です。
計算するには、[ 超投影法] を選択し、次のオプションを設定します。
サンプルの数
使用するサンプルの数を示す整数を入力します。 既定値は 9 です。成功数
成功の値を定義する整数を入力します。 既定値は 24 です。母集団のサイズ
超幾何分布を推定するときに使用する、母集団のサイズを指定します。
ラプラス
Laplace 分布は、平均とスケール パラメーターによってパラメーター化された実数に対する分布です。
計算するには、 Laplace 分布を選択し、次のオプションを設定します。
スケール
分布のスケーリングで使用する値を入力します。スケールの値を分布に適用すると、分布を縮小または拡大できます。
既定値は 1.0 です。 値は正の数値にする必要があります。
場所
0番目の要素の位置を表す数値 (double) を入力します。Location パラメーターの値を入力して、確率分布を数値スケールの上下へ移動することができます。
既定では、0.0 です。
ロジスティック
ロジスティック分布は正規分布に似ていますが、分布の左側には制限がありません。 ロジスティック分布は、ロジスティック回帰およびニューラル ネットワーク モデルで使用され、また生命科学データのモデリングでも使用されます。
計算するには、 ロジスティックを選択し、次のオプションを設定します。
スケール
分布のスケーリングで使用する値を入力します。スケールの値を分布に適用すると、分布を縮小または拡大できます。
既定値は 1.0 です。 値は正の数値にする必要があります。
Mean (平均値)
分布の推定平均値を示す数値 (double) を入力します。 既定では、0.0 です。
対数正規
対数正規分布は、連続一変量分布です。
計算するには、[ Lognormal] を選択し、次のオプションを設定します。
Mean (平均値)
分布の推定平均値を示す数値 (double) を入力します。 既定では、0.0 です。標準偏差
分布の推定標準偏差を示す正の数値 (double) を入力します。 既定値は 1.0 です。
NegativeBinomial
負の二項分布は、2 つのパラメーター (r、p) を持つ自然数に関する分布です。 整数の r 特殊なケースでは、ヘッドの確率が p の場合に、r番目 のヘッドの前の尾の数として分布を解釈できます。
計算するには、 NegativeBinomial を選択し、次のオプションを設定します。
成功率
成功率を示す 0.0 ~ 1.0 の数値 (float) を入力します。 既定値は .5 です。成功数
成功の値を指定する整数を入力します。 既定値は 24 です。
標準
正規分布はガウス分布とも呼ばれます。
計算するには、[ 標準]を選択し、次のオプションを設定します。
Mean (平均値)
分布の推定平均値を示す数値 (double) を入力します。 既定では、0.0 です。標準偏差
分布の推定標準偏差を示す正の数値 (double) を入力します。 既定値は 1.0 です。
パレート
パレート分布は、ソーシャル、科学、地球物理、保険数理、その他さまざまな種類の観測可能な現象と一致する、べき乗確率分布です。
計算するには、 パレートを選択し、次のオプションを設定します。
図形
値を入力して (省略可能)、分布の形状を変更します。形状のパラメーターは、形状の位置またはスケールを定義しない、確率分布のパラメーターです。 そのため、形状の値を入力すると、パラメーターは分布を移動したり、拡大または縮小したりするのではなく、分布の形状を変更します。
値は数値 (
double) である必要があります。 既定値は 1.0 です。スケール
分布のスケールを変更するには、値 (省略可能) を入力します。 スケールの値を分布に適用すると、分布を縮小または拡大できます。値は数値 (
double) である必要があります。 既定値は 1.0 です。
ポワソン
この実装では、クヌースの手法を使用してポワソン分布の確率変数を生成します。 ポアソン分布の詳細については、「 ポアソン回帰」を参照してください。
計算するには、 ポアソンを選択し、次のオプションを設定します。
- Mean (平均値)
分布の推定平均値を示す数値 (double) を入力します。 既定では、0.0 です。
レイリー
レイリー分布は、連続確率分布です。 この分布が現れる例として、2 次元風速成分ベクトルに相関関係がなく、等分散によって正規分布している場合に、風速がレイリー分布を持つことが挙げられます。
計算するには、 Rayleigh を選択し、次のオプションを設定します。
- 下限
分布の下限を表す数値 (double) を入力します。 既定では、0.0 です。
StandardNormal
このオプションは標準正規分布を提供し、他のパラメータは提供しません。
計算するには、 StandardNormal を選択し、列を選択します。
TStudent
このオプションは、一変量学生の t 分布を実装します。
計算するには、 TStudent を選択し、次のオプションを設定します。
- 自由度数
自由度を指定する数値doubleを入力します。 既定値は 1.0 です。
TStudentRightTailed
1 つの右裾を使用して一変量のスチューデントの t 分布を実装します。
計算するには、 TStudentRightTailed を選択し、次のオプションを設定します。
- 自由度数
自由度を指定する数値doubleを入力します。 既定値は 1.0 です。
TStudentTwoTailed
スチューデントの両側 t 分布を実装します。
計算するには、 TStudentTwoTailed を選択し、次のオプションを設定します。
- 自由度数
自由度を指定する数値doubleを入力します。 既定値は 1.0 です。
Uniform
一様分布は、四角形分布とも呼ばれます。
計算するには、 Uniform を選択し、次のオプションを設定します。
下限
分布の下限を表す数値 (double) を入力します。 既定では、0.0 です。上限
分布の上限を表す数値 (double) を入力します。 既定値は 1.0 です。
ワイブル
ワイブル分布は信頼性工学で広く使用されます。 その Shape パラメーターを使用して、他の多くの分布をモデル化できます。
計算するには、[ ワイブル] を選択し、次のオプションを設定します。
図形
値を入力して (省略可能)、分布の形状を変更します。形状のパラメーターは、形状の位置またはスケールを定義しない、確率分布のパラメーターです。 そのため、形状の値を入力すると、パラメーターは分布を移動したり、拡大または縮小したりするのではなく、分布の形状を変更します。
値は数値 (
double) である必要があります。 既定値は 1.0 です。スケール
分布のスケールを変更するには、値 (省略可能) を入力します。 スケールの値を分布に適用すると、分布を縮小または拡大できます。値は数値 (
double) である必要があります。 既定値は 1.0 です。
テクニカル ノート
このセクションには、実装の詳細、ヒント、よく寄せられる質問への回答が含まれています。
実装の詳細
このモジュールでは、オープン ソース MATH.NET Numerics ライブラリで提供するすべての分布をサポートしています。 詳細については、 Math.Net.Numerics.Distribution ライブラリのドキュメントを参照してください。
右辺と両側のディストリビューションは、基本ディストリビューションのパラメーター化されたバージョンとしてではなく、個別のディストリビューションとして表示されます。 現状の動作により、Excel との互換性を維持しています。
定義
このモジュールでは、指定した分布に対して次のいずれかの値を計算できます。
cdf、または 累積分布関数
複合イベントの確率を返します。ランダム変数が特定の値 x より小さい値を受け取る場合の再帰の合計として定義されます。
つまり、"この値以下のサンプルはどのくらい一般的ですか" という質問に答えます。
この関数は、連続数値変数と不連続数値変数の両方で使用できます。
InverseCdf、または 逆累積分布関数
特定の累積確率値 (cdf) に関連付けられている値を返します。
つまり、"cdf 関数が累積確率 y を返す x の値は何ですか" という質問に答えます。
pdf、または 確率密度関数
ランダム変数が特定の値になる相対的な可能性について説明します。
言い換えると、"サンプルは正確にこの値でどれくらい一般的か" という質問に答えます。
想定される入力
| 名前 | Type | 説明 |
|---|---|---|
| データセット | データ テーブル | 入力データセット |
モジュールのパラメーター
| 名前 | Range | Type | Default | 説明 |
|---|---|---|---|---|
| Distribution | Any | ProbabilityDistribution | StandardNormal | 生成する確率分布の種類を選択します。 |
| メソッド | Any | ProbabilityDistributionMethod | Cdf | 選択した確率分布を計算するときに使用する方法を選択します。 オプションは、累積分布関数 (cdf)、逆累積分布関数 (InverseCdf)、および確率密度関数または質量関数 (pdf) です。 |
| 負の二項分布法 | Any | ProbabilityDistributionMethodForNegativeBinomial | Cdf | 負の二項分布を選択する場合は、分布を評価するために使用する方法を指定します。 |
| 成功率 | [0.0;1.0] | Float | 0.5 | 成功率として使用する値を入力します。 |
| 図形 | Any | Float | 1.0 | 分布の形状を変更する値を入力します。 |
| スケール | >=0.0 | Float | 1.0 | 分布のスケールを変更する値を入力し、分布のサイズを拡大または縮小します。 |
| 試行回数 | >=1 | Integer | 3 | 試行回数を指定します。 |
| 下限 | Any | Float | 0.0 | 分布の下限として使用する数値を入力します。 |
| 上限 | Any | Float | 1.0 | 分布の上限として使用する数値を入力します。 |
| 場所 | Any | Float | 0.0 | 分布の 0 個の要素の位置を入力します。 |
| 自由度数 | Any | Float | 1.0 | 自由度の数を指定します。 |
| 分子の自由度 | Any | Float | 3.0 | 分子に自由度の数を指定します。 |
| 分母の自由度 | Any | Float | 6.0 | 分母に自由度の数を指定します。 |
| Lambda | >=0.0 | Float | 1.0 | Lambda パラメーターの値を指定します。 |
| サンプル数 | Any | Integer | 9 | サンプルの数を指定します。 |
| 成功数 | Any | Integer | 24 | 成功数として使用する値を入力します。 |
| 母集団のサイズ | Any | Integer | 52 | 母集団のサイズを指定します。 |
| 平均 | Any | Float | 0.0 | 推定される平均値を入力します。 |
| 標準偏差 | >=0.0 | Float | 1.0 | 推定される標準偏差を入力します。 |
| 列セット | Any | ColumnSelection | 確率分布の計算対象となる列を選択します。 | |
| 結果モード | Any | OutputTo | ResultOnly | 出力データセットに結果を保存する方法を指定します。 オプションにより、新しい列を追加、既存の列を置換、または結果だけを出力できます。 |
出力
| 名前 | Type | 説明 |
|---|---|---|
| 結果のデータセット | データ テーブル | 出力データセット |
例外
エラー メッセージの完全な一覧については、「 モジュール エラー コード」を参照してください。
| 例外 | 説明 |
|---|---|
| エラー 0017 | 指定した 1 つまたは複数の列に、現在のモジュールでサポートされていない型がある場合、例外が発生します。 |
Studio (クラシック) モジュールに固有のエラーの一覧については、「Machine Learningエラー コード」を参照してください。
API 例外の一覧については、「REST API エラー コードMachine Learning」を参照してください。