Teoria do algoritmo de busca de Grover
Neste artigo, você encontrará uma explicação teórica detalhada dos princípios matemáticos que fazem o algoritmo de Grover funcionar.
Para uma implementação prática do algoritmo de Grover para resolver problemas matemáticos, consulte Implementar o algoritmo de pesquisa de Grover.
Declaração do problema
O algoritmo de Grover acelera a solução para pesquisas de dados não estruturados (ou problema de pesquisa), executando a pesquisa em menos etapas do que qualquer algoritmo clássico poderia. Qualquer tarefa de pesquisa pode ser expressa com uma função $abstrata f(x)$ que aceita itens $de pesquisa x$. Se o item $x$ for uma solução para a tarefa de pesquisa, f $(x)=1$. Se o item $x$ não for uma solução, f $(x)=0$. O problema de pesquisa consiste em encontrar qualquer item $x_0$ tal que $f(x_0)=1$.
Na verdade, qualquer problema que lhe permita verificar se um determinado valor $x$ é uma solução válida (uma &cotação; sim ou não problema") pode ser formulado em termos do problema de pesquisa. Seguem-se alguns exemplos:
- Problema de satisfatibilidade booleana: O conjunto de valores $booleanos x$ é uma interpretação (uma atribuição de valores a variáveis) que satisfaz a fórmula booleana dada?
- Problema do caixeiro-viajante: x $$ descreve o loop mais curto possível que liga todas as cidades?
- Problema de pesquisa de banco de dados: A tabela do banco de dados contém um registro $x$?
- Problema de fatoração de inteiros: O número $fixo N$ é divisível pelo número $x$?
A tarefa que o algoritmo de Grover pretende resolver pode ser expressa da seguinte forma: dada uma função $clássica f(x):\{0,1\}^n \rightarrow\{0,1\}$, onde $n$ é o tamanho de bit do espaço de pesquisa, encontre um x_0$ de entrada $para o qual $f(x_0)=1$. A complexidade do algoritmo é medida pelo número de usos da função $f(x)$. Classicamente, no pior cenário, $f(x)$ tem que ser avaliado um total de $N-1$ vezes, onde $N=2^n$, experimentando todas as possibilidades. Depois $dos elementos N-1$ , deve ser o último elemento. O algoritmo quântico de Grover pode resolver esse problema muito mais rápido, fornecendo uma velocidade quadrática. Quadrático aqui implica que apenas cerca $\sqrt{de N}$ avaliações seriam necessárias, em comparação com $N$.
Descrição geral do algoritmo
Suponha que há $N=2^n$ itens qualificados para a tarefa de pesquisa e eles são indexados atribuindo a cada item um inteiro de $0$ a $N-1$. Além disso, suponha que existem $entradas válidas M$ diferentes, o que significa que há $entradas M$ para as quais $f(x)=1$. As etapas do algoritmo são as seguintes:
- Comece com um registro de $n$ qubits inicializados no estado $\ket{0}$.
- Preparar o registo numa sobreposição uniforme aplicando $H a cada qubit do registo: $$|\text{registar}\rangle=\frac{1}{\sqrt{N}}\sum_{x=0}^{N-1}|$ x\rangle$$
- Aplique as seguintes operações ao registro $N_{\text{horários ideais}}$ :
- O oráculo $de fase O_f$ que aplica um deslocamento de fase condicional de -1$ para os itens de $solução.
- Aplique $H$ a cada qubit no registo.
- Um deslocamento de fase condicional de -1$ para todos os estados de $base computacional, exceto $\ket{0}$. Isso pode ser representado pela operação $unitária -O_0$, pois $O_0$ representa o deslocamento de fase condicional para $\ket{0}$ apenas.
- Aplique $H$ a cada qubit no registo.
- Meça o registro para obter o índice de um item que é uma solução com probabilidade muito alta.
- Verifique se é uma solução válida. Se não, comece de novo.
$N_\text{optimal}=\left\lfloor \frac{\pi{4}\sqrt{\frac{}{N}{M}}-{2}\frac{1}{\right\rfloor$ é o número ideal de iterações que maximiza a probabilidade de obter o item correto medindo o registro.
Nota
A aplicação conjunta dos passos 3.b, 3.c e 3.d é geralmente conhecida na literatura como operador de difusão de Grover.
A operação unitária global aplicada ao registo é a seguinte:
$$(-H^{\otimes n}O_0H^{\otimes n}O_f)^{N_{\text{ótimo}}}H^{\otimes n}$$
Seguir passo a passo o estado do registo
Para ilustrar o processo, vamos seguir as transformações matemáticas do estado do registro para um caso simples em que há apenas dois qubits e o elemento válido é $\ket{01}.$
O cadastro começa no estado: $$|\text{registro}\rangle=|00\rangle$$
Depois de aplicar $H$ a cada qubit, o estado do registro se transforma em: $$|\text{register}\rangle\frac{\sum{1}{\sqrt{{4}}=_{i \in \{0,1\}^2}|i\rangle=\frac12(\ket{00}+\ket{01}+\ket{10}+)\ket{11}$$
Em seguida, a fase oracle é aplicada para obter: $$|\text{registrar}\rangle=\frac12(\ket{{00}-\ket{{01}+\ket{{10}+\ket{{11})$$
Em seguida, $H age em cada qubit novamente para dar: $$|\text{registre}\rangle=\frac12(\ket{{00}+\ket{{01}-\ket{{10}+\ket{{11})$$$
Agora, o deslocamento de fase condicional é aplicado em todos os estados, exceto $\ket{00}$: $$|\text{registro}\rangle\frac=12(\ket{{00}-\ket{{01}+{10}\ket{-)\ket{{11}$$
Finalmente, a primeira iteração Grover termina aplicando $H$ novamente para obter: $$|\text{registrar}\rangle=\ket{{01}$$
Seguindo as etapas acima, o item válido é encontrado em uma única iteração. Como você verá mais adiante, isso ocorre porque para N=4 e um único item válido, $N_\text{ótimo}=1$.
Explicação geométrica
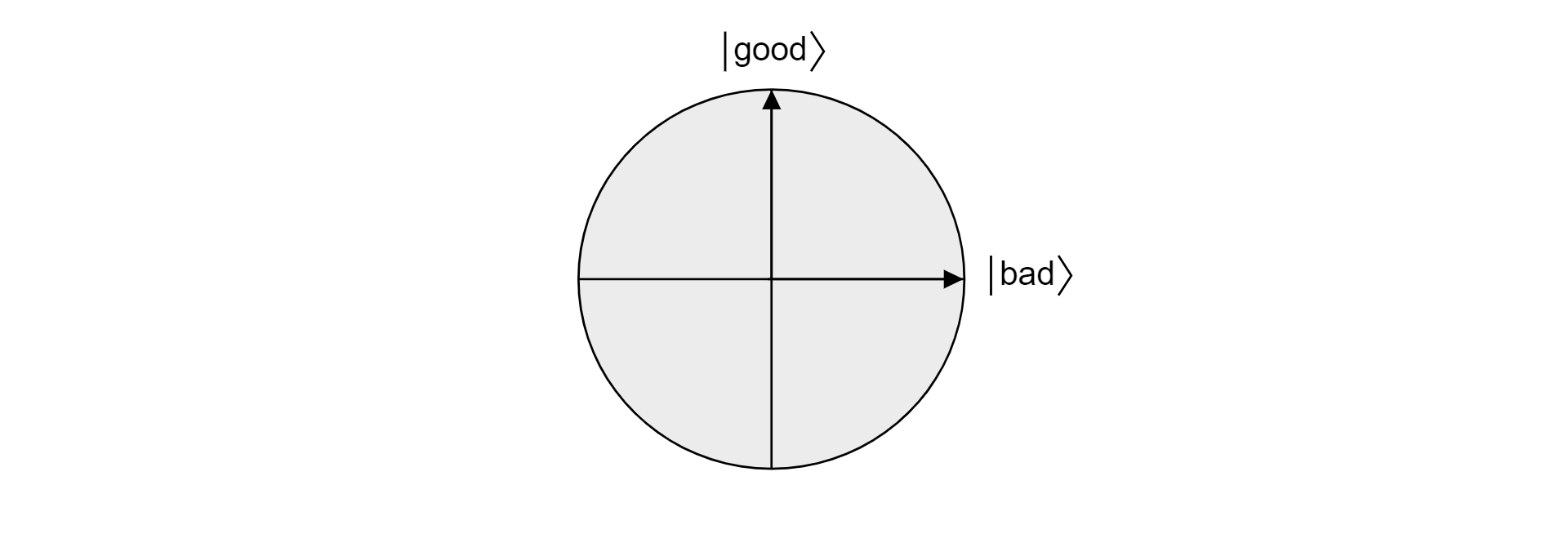
Para ver por que o algoritmo de Grover funciona, vamos estudar o algoritmo de uma perspetiva geométrica. Que $\ket{\text{}}$ seja ruim a sobreposição de todos os estados que não são uma solução para o problema de busca. Supondo que existam $soluções válidas M$ :
$$\ket{\text{ruim}}=\frac{{1}{\sqrt{N-M}}\sum_{x:f(x)=0}\ket{x}$$
O bem}}$ estatal $\ket{\text{é definido como a sobreposição de todos os estados que são uma solução para o problema de pesquisa:
$$\ket{\text{bom}}=\frac{{1}{\sqrt{M}}\sum_{x:f(x)=1}\ket{x}$$
Uma vez que o bom e o mau são conjuntos mutuamente exclusivos porque um item não pode ser válido e não válido, os estados $\ket{\text{bom}}$ e $\ket{\text{mau}}$ são ortogonais. Ambos os estados formam a base ortogonal de um plano no espaço vetorial. Pode-se usar este plano para visualizar o algoritmo.
Agora, suponhamos $\ket{\psi}$ que é um estado arbitrário que vive no plano atravessado pelo bem}}$ e $\ket{\text{pelo $\ket{\text{mal}}$. Qualquer estado que viva nesse plano pode ser expresso como:
$$\ket{\psi}=\alpha\ket{\text{bom}} + \beta\ket{\text{mau}}$$
onde $\alpha$ e $\beta$ são números reais. Agora, vamos apresentar o operador $de reflexão R_{\ket{\psi}}$, onde $\ket{\psi}$ está qualquer estado de qubit vivendo no avião. O operador é definido como:
$$R_{\ket{\psi}}=2\ket{\psi}\bra{\psi}-\mathcal{I}$$
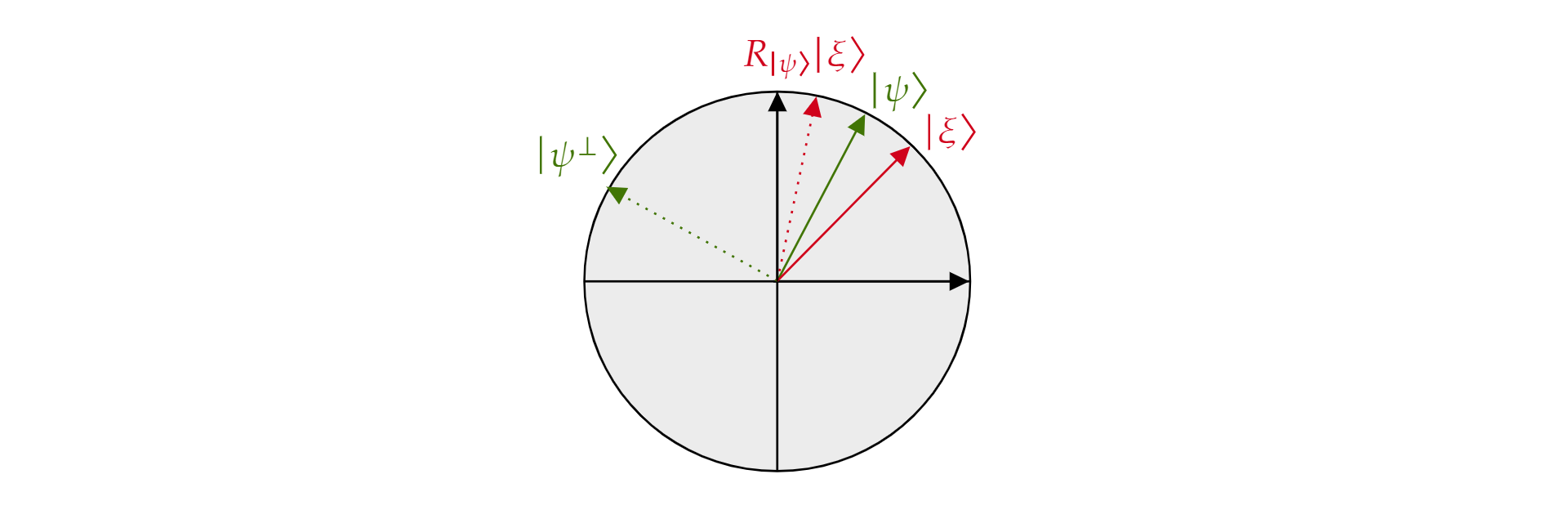
É chamado de operador de reflexão sobre $\ket{\psi}$ porque pode ser geometricamente interpretado como reflexão sobre a direção de $\ket{\psi}$. Para vê-lo, pegue a base ortogonal do plano formado por $\ket{\psi}$ e seu complemento $\ket{\psiortogonal ^{\perp}}$. Qualquer estado $\ket{\xi}$ do plano pode ser decomposto em tal base:
$$\ket{\xi}=\mu \ket{\psi} + \nu {\ket{\psi^{\perp}}}$$
Se se aplicar o operador $R_{\ket{\psi}}$ a $\ket{\xi}$:
$$R_{\ket{\psi}}\ket{\xi}=\mu \ket{\psi} - \nu {\ket{\psi^{\perp}}}$$
O operador $R_\ket{\psi}$ inverte o componente ortogonal $\ket{\psi}$ , mas deixa o $\ket{\psi}$ componente inalterado. Portanto, $R_\ket{\psi}$ é uma reflexão sobre $\ket{\psi}$.
O algoritmo de Grover, após a primeira aplicação de $H$ a cada qubit, começa com uma superposição uniforme de todos os estados. Isto pode ser escrito como:
$$\ket{\text{todos M}}\sqrt{\frac{=}{N}}\ket{\text{bom}} + \sqrt{\frac{N-M}{N mau}}\ket{\text{}}$$
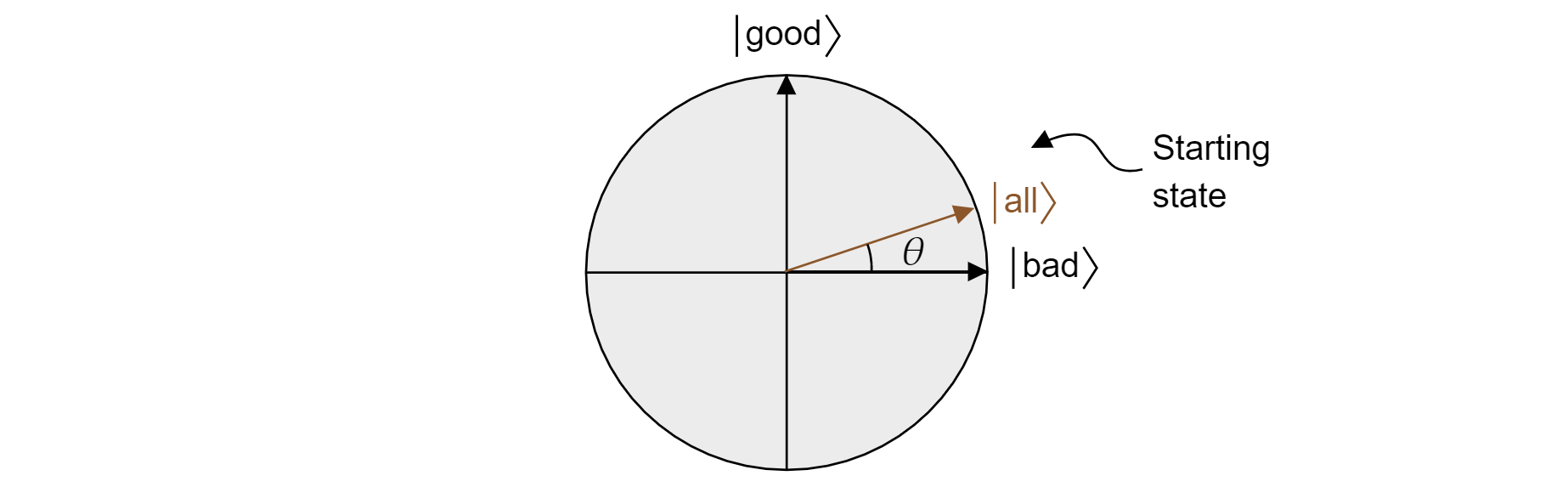
E assim o Estado vive no avião. Note que a probabilidade de obter um resultado correto ao medir a partir da superposição igual é apenas boa all^2=M/N$, que é o que você esperaria de um palpite aleatório.}}}|}|{\text{$|\braket{\text{
O oráculo $O_f$ adiciona uma fase negativa a qualquer solução para o problema de pesquisa. Portanto, pode ser escrito como uma reflexão sobre o $\ket{\text{eixo ruim}}$ :
$$= O_f R_{\ket{\text{ruim=}}} 2\ket{\text{ruim}}\bra{\text{}} - \mathcal{I}$$
Analogamente, o deslocamento $de fase condicional O_0$ é apenas uma reflexão invertida sobre o estado $\ket{0}$:
$$O_0 R_{\ket{0}}= -2\ket{{0}\bra{0} + \mathcal{I =}$$
Sabendo deste fato, é fácil verificar que a operação $de difusão Grover -H^{\otimes n} O_0 H^{\otimes n}$ é também uma reflexão sobre o estado $\ket{todo}$. Basta fazer:
$$-H^{\otimes n} O_0 H^{\otimes n}=2H^{\otimes n{0}}\ket{0}\bra{H^{\otimes n} -H^{\otimes n}\mathcal{I}H^{\otimes n}= 2\ket{\text{todos}}}}\bra{\text{ - \mathcal{I}= R_{\ket{\text{all}}}$$
Foi demonstrado que cada iteração do algoritmo de Grover é uma composição de duas reflexões $R_\ket{\text{bad}}$ e $R_\ket{\text{all}}$.
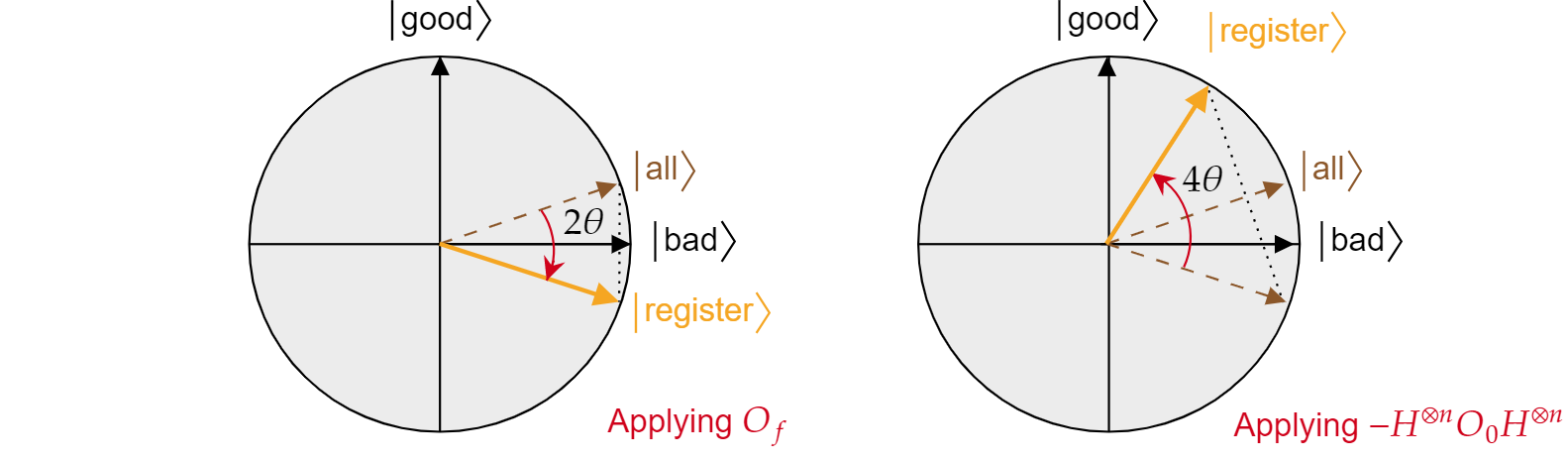
O efeito combinado de cada iteração Grover é uma rotação no sentido anti-horário de um ângulo $2\theta$. Felizmente, o ângulo $\theta$ é fácil de encontrar. Como $\theta$ é apenas o ângulo entre $\ket{\text{tudo e $\ket{\text{ruim}}$}}$, pode-se usar o produto escalar para encontrar o ângulo. Sabe-se que $\cos{\theta}=\braket{\text{tudo}|\text{de ruim}}$, então é preciso calcular $\braket{\text{tudo}|\text{de ruim}}$. Da decomposição de $\ket{\text{todos}}$ em termos de $\ket{\text{mau}}$ e $\ket{\text{bom}}$, segue-se:
$$\theta = \arccos{\left(\braket{\text{tudo}|\text{ruim}}\right)}= \arccos{\left(\sqrt{\frac{N-M}{N}}\right)}$$
O ângulo entre o estado do registo e o $\ket{\text{estado bom}}$ diminui a cada iteração, resultando numa maior probabilidade de medir um resultado válido. Para calcular essa probabilidade, você só precisa calcular $|\braket{\text{um bom}|\text{registro}}|^2$. Denotando o ângulo entre $\ket{\text{bom}}$ e $\ket{\text{registro}}$$\gamma (k),$ onde $k$ é a contagem de iteração:
$$\gamma (k) =\frac{\pi}{2}-\theta -k2\theta =\frac{\pi}{{2} -(2k + 1) \theta $$
Portanto, a probabilidade de sucesso é:
$$P(\text{sucesso}) = \cos^2(\gamma(k)) = \sin^2\left[(2k +1)\arccos \left( \sqrt{\frac{N-M}{N}}\right)\right]$$
Número ideal de iterações
Como a probabilidade de sucesso pode ser escrita em função do número de iterações, o número ótimo de iterações $N_{\text{ótimo}}$ pode ser encontrado calculando o menor número inteiro positivo que (aproximadamente) maximiza a função de probabilidade de sucesso.
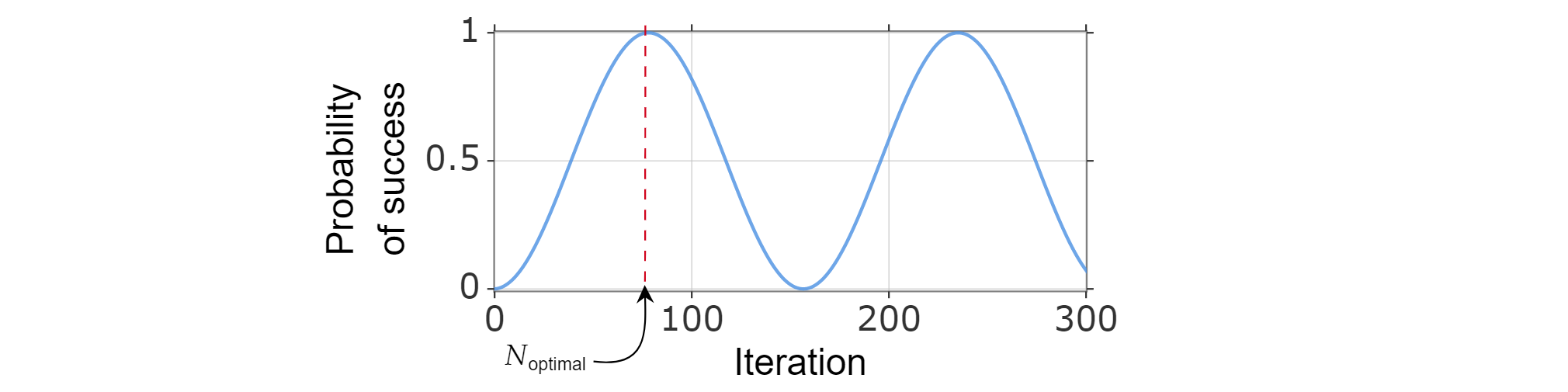
Sabe-se que $\sin^2{x}$ atinge seu primeiro máximo para $x=\frac{\pi}{2}$, assim:
$$\frac{\pi}{{2}=(2k_{\text{ótimo}} +1)\arccos \left( \sqrt{\frac{N-M}{N}}\right)$$
Isto dá:
$$k_{\text{ótimo}}=\frac{\pi}{4\arccos\left(\sqrt{1-M/N}\right)}-1/2\frac{= \pi}{{4}\sqrt{\frac{N}{M}}-\frac{1}{2}-O\left(\sqrt\frac{M}{N)}\right$$
Onde na última etapa, $\arccos \sqrt{1-x=\sqrt{}x} + O(x^{3/2})$.
Portanto, você pode escolher $N_\text{ideal}$ para ser $N_\text{ótimo\left}=\lfloor \frac{\pi}{{4}\sqrt{\frac{N}{M}}-{1}{2}\frac{\right\rfloor.$
Análise da complexidade
A partir da análise anterior, $consultas O\left(\sqrt{\frac{N}{M}}\right)$ do oráculo $O_f$ são necessárias para encontrar um item válido. No entanto, o algoritmo pode ser implementado de forma eficiente em termos de complexidade de tempo? $$ O_0 é baseado na computação de operações booleanas em $n$ bits e é conhecido por ser implementável usando $portas O(n$). Há também duas camadas de $portões n$ Hadamard. Ambos os componentes, portanto, requerem apenas $portas O(n)$ por iteração. Porque $N=2^n$, segue-se que $O(n)=O(log(N)).$ Portanto, se $iterações O\left(\sqrt{\frac{N}{M}}\right)$ e $portas O(log(N))$ por iteração forem necessárias, a complexidade de tempo total (sem levar em conta a implementação oracle) será $O\left(\sqrt{\frac{N}{M}}log(N)\right).$
A complexidade geral do algoritmo depende, em última análise, da complexidade da implementação do oracle $O_f$. Se uma avaliação de função é muito mais complicada em um computador quântico do que em um clássico, o tempo de execução geral do algoritmo será mais longo no caso quântico, embora tecnicamente, ele use menos consultas.
Referências
Se você quiser continuar aprendendo sobre o algoritmo de Grover, você pode verificar qualquer uma das seguintes fontes:
- Artigo original de Lov K. Grover
- Seção de algoritmos de busca quântica de Nielsen, M. A. & Chuang, I. L. (2010). Computação Quântica e Informação Quântica.
- O algoritmo de Grover em Arxiv.org